Question Number 43937 by abdo.msup.com last updated on 18/Sep/18
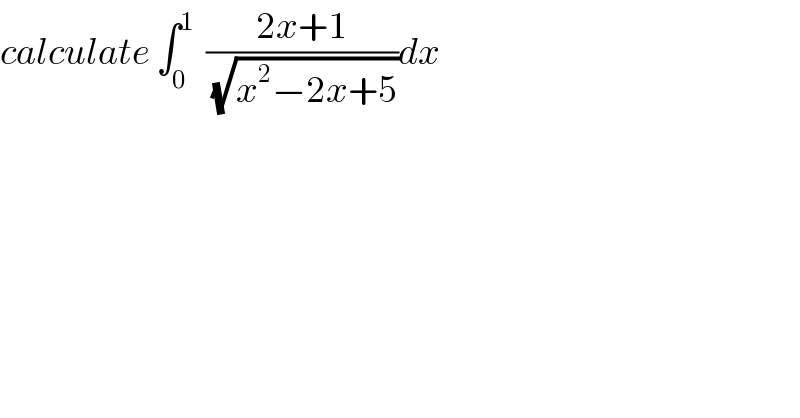
$${calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{5}}}{dx} \\ $$
Commented by maxmathsup by imad last updated on 19/Sep/18
![let A = ∫_0 ^1 ((2x+1)/( (√(x^2 −2x+5)))) wehave x^2 −2x+5=(x−1)^2 +4 changement x−1 =2sh(t)give I = ∫_(argsh(−(1/2))) ^0 ((2(1+2sh(t)))/(2ch(t))) 2ch(t)dt = [2t]_(ln( −(1/2)+(√( (5/4))))) ^0 +4 [sh]_(ln(((−1)/2)+(√(5/4)))) ^0 =−(((−1+(√5))/2))^2 +4[((e^u −e^(−u) )/2)]_(ln(((−1+(√5))/2))) ^0 =−(((−1+(√5))/2))^2 +4{((−1+(√5))/2) −(((−1+(√5))/2))^(−1) }](https://www.tinkutara.com/question/Q43979.png)
$${let}\:{A}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{5}}}\:{wehave}\:{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{5}=\left({x}−\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{4}\:{changement} \\ $$$${x}−\mathrm{1}\:=\mathrm{2}{sh}\left({t}\right){give}\:{I}\:=\:\int_{{argsh}\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)} ^{\mathrm{0}} \:\:\frac{\mathrm{2}\left(\mathrm{1}+\mathrm{2}{sh}\left({t}\right)\right)}{\mathrm{2}{ch}\left({t}\right)}\:\mathrm{2}{ch}\left({t}\right){dt} \\ $$$$=\:\left[\mathrm{2}{t}\right]_{{ln}\left(\:−\frac{\mathrm{1}}{\mathrm{2}}+\sqrt{\:\frac{\mathrm{5}}{\mathrm{4}}}\right)} ^{\mathrm{0}} \:\:\:\:\:\:+\mathrm{4}\:\left[{sh}\right]_{{ln}\left(\frac{−\mathrm{1}}{\mathrm{2}}+\sqrt{\frac{\mathrm{5}}{\mathrm{4}}}\right)} ^{\mathrm{0}} \\ $$$$=−\left(\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\mathrm{4}\left[\frac{{e}^{{u}} −{e}^{−{u}} }{\mathrm{2}}\right]_{{ln}\left(\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)} ^{\mathrm{0}} \:=−\left(\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\mathrm{4}\left\{\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\:−\left(\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{−\mathrm{1}} \right\} \\ $$$$ \\ $$
Answered by sma3l2996 last updated on 19/Sep/18
![x^2 −2x+5=(x−1)^2 +4=4((((x−1)/2))^2 +1) let′s take t=((x−1)/2)⇒dx=2dt ∫_0 ^1 ((2x+1)/( (√(x^2 −2x+5))))dx=∫_(−1/2) ^0 ((2(2t+1)+1)/(2(√(t^2 +1))))(2dt) =∫_(−1/2) ^0 ((4t+3)/( (√(t^2 +1))))dt t=sinhu⇒dt=coshudu A=∫_0 ^1 ((2x+1)/( (√(x^2 −2x+5))))dx=∫_(sinh^(−1) (−1/2)) ^0 ((4sinh(u)+1)/( (√(sinh^2 u+1))))(coshudu) =∫_(sinh^(−1) (−1/2)) ^0 ((4sinhu+1)/(coshu))(coshudu) =∫_(sinh(−1/2)) ^0 (4sinhu+1)du =[4coshu+u]_(sinh(−1/2)) ^0 =4−4cosh(sinh^(−1) (((−1)/2)))−sinh^(−1) (((−1)/2)) sinh^(−1) (−1/2)=ln((√3)−1)−ln(2) cosh(sinh^(−1) (((−1)/2)))=((√3)/2) So A=4+ln2−ln((√3)−1)−2(√3)](https://www.tinkutara.com/question/Q43960.png)
$${x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{5}=\left({x}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{4}=\mathrm{4}\left(\left(\frac{{x}−\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{1}\right) \\ $$$${let}'{s}\:{take}\:\:{t}=\frac{{x}−\mathrm{1}}{\mathrm{2}}\Rightarrow{dx}=\mathrm{2}{dt} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{5}}}{dx}=\int_{−\mathrm{1}/\mathrm{2}} ^{\mathrm{0}} \frac{\mathrm{2}\left(\mathrm{2}{t}+\mathrm{1}\right)+\mathrm{1}}{\mathrm{2}\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}}\left(\mathrm{2}{dt}\right) \\ $$$$=\int_{−\mathrm{1}/\mathrm{2}} ^{\mathrm{0}} \frac{\mathrm{4}{t}+\mathrm{3}}{\:\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}}{dt} \\ $$$${t}={sinhu}\Rightarrow{dt}={coshudu} \\ $$$${A}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{5}}}{dx}=\int_{{sinh}^{−\mathrm{1}} \left(−\mathrm{1}/\mathrm{2}\right)} ^{\mathrm{0}} \frac{\mathrm{4}{sinh}\left({u}\right)+\mathrm{1}}{\:\sqrt{{sinh}^{\mathrm{2}} {u}+\mathrm{1}}}\left({coshudu}\right) \\ $$$$=\int_{{sinh}^{−\mathrm{1}} \left(−\mathrm{1}/\mathrm{2}\right)} ^{\mathrm{0}} \frac{\mathrm{4}{sinhu}+\mathrm{1}}{{coshu}}\left({coshudu}\right) \\ $$$$=\int_{{sinh}\left(−\mathrm{1}/\mathrm{2}\right)} ^{\mathrm{0}} \left(\mathrm{4}{sinhu}+\mathrm{1}\right){du} \\ $$$$=\left[\mathrm{4}{coshu}+{u}\right]_{{sinh}\left(−\mathrm{1}/\mathrm{2}\right)} ^{\mathrm{0}} =\mathrm{4}−\mathrm{4}{cosh}\left({sinh}^{−\mathrm{1}} \left(\frac{−\mathrm{1}}{\mathrm{2}}\right)\right)−{sinh}^{−\mathrm{1}} \left(\frac{−\mathrm{1}}{\mathrm{2}}\right) \\ $$$${sinh}^{−\mathrm{1}} \left(−\mathrm{1}/\mathrm{2}\right)={ln}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)−{ln}\left(\mathrm{2}\right) \\ $$$${cosh}\left({sinh}^{−\mathrm{1}} \left(\frac{−\mathrm{1}}{\mathrm{2}}\right)\right)=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$${So}\:{A}=\mathrm{4}+{ln}\mathrm{2}−{ln}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)−\mathrm{2}\sqrt{\mathrm{3}} \\ $$$$ \\ $$
