Question Number 62419 by mathmax by abdo last updated on 20/Jun/19
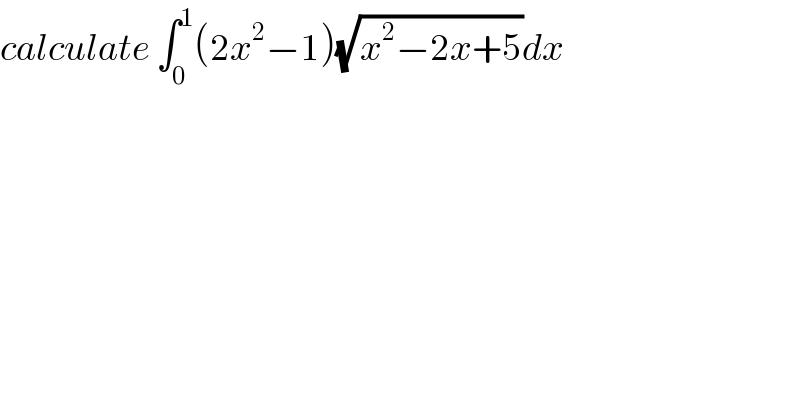
$${calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{2}{x}^{\mathrm{2}} −\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{5}}{dx} \\ $$
Commented by mathmax by abdo last updated on 21/Jun/19
![let I =∫_0 ^1 (2x^2 −1)(√(x^2 −2x+5))dx we have x^2 −2x+5 =x^2 −2x+1+4 =(x−1)^2 +4 let use the changement (x−1) =2sh(t) ⇒x =2sh(t)+1 I = ∫_(argsh(−(1/2))) ^0 {2 (2sh(t)+1)^2 −1}2 ch(t) 2ch(t)dt =4 ∫_(ln(−(1/2)+(√(5/4)))) ^0 {2(4sh^2 t +4sht +1)−1}ch^2 (t)dt =4∫_(ln(((−1+(√5))/2))) ^0 { 8sh^2 t+8sh(t)+1}ch^2 t dt =32 ∫_(ln(((−1+(√5))/2))) ^0 sh^2 t ch^2 t dt +32 ∫_(ln(((−1+(√5))/2))) ^0 sh(t)ch^2 (t)dt +4 ∫_(ln(((−1+(√5))/2))) ^0 ch^2 (t)dt ∫_(ln(((−1+(√5))/2))) ^0 (shtcht)^2 dt =(1/4) ∫_(ln(((−1+(√5))/2))) ^0 sh(2t)dt =(1/8)[ch(2t)]_(ln(((−1+(√5))/2))) ^0 =(1/(16))[ e^(2t) +e^(−2t) ]_(ln(((−1+(√5))/2))) ^0 =(1/(16)){ 2 −(((−1+(√5))/2))^2 −(1/((((−1+(√5))/2))^2 ))} ∫_(ln(((−1+(√5))/2))) ^0 sh(t)ch^2 (t)dt =[(1/3)ch^3 t]_(ln(((−1+(√5))/2))) ^0 =(1/3)[ (((e^t +e^(−t) )/2))^3 ]_(ln(((−1+(√5))/2))) ^0 =(1/(24)){ 8 − { (((−1+(√5))/2))−(1/((−1+(√5))/2))}^3 } . ∫_(ln(((−1+(√5))/2))) ^0 ch^2 t dt =(1/2) ∫_(ln(((−1+(√5))/2))) ^0 (1+ch(2t))dt =−(1/2)ln(((−1+(√5))/2)) +(1/4)[sh(2t)]_(ln(((−1+(√5))/2))) ^0 =−(1/2)ln(((−1+(√5))/2))+(1/8)[ e^(2t) −e^(−2t) ]_(ln(((−1+(√5))/2))) ^0 =−(1/2)ln(((−1+(√5))/2)) +(1/8){−(((−1+(√5))/2))^2 +(1/((((−1+(√5))/2))^2 ))} the value of I is known .](https://www.tinkutara.com/question/Q62490.png)
$${let}\:{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{2}{x}^{\mathrm{2}} −\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{5}}{dx}\:\:\:{we}\:{have}\:{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{5}\:={x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}+\mathrm{4}\:=\left({x}−\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{4} \\ $$$${let}\:{use}\:{the}\:{changement}\:\left({x}−\mathrm{1}\right)\:=\mathrm{2}{sh}\left({t}\right)\:\Rightarrow{x}\:=\mathrm{2}{sh}\left({t}\right)+\mathrm{1} \\ $$$${I}\:=\:\int_{{argsh}\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)} ^{\mathrm{0}} \:\left\{\mathrm{2}\:\left(\mathrm{2}{sh}\left({t}\right)+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}\right\}\mathrm{2}\:{ch}\left({t}\right)\:\mathrm{2}{ch}\left({t}\right){dt} \\ $$$$=\mathrm{4}\:\int_{{ln}\left(−\frac{\mathrm{1}}{\mathrm{2}}+\sqrt{\frac{\mathrm{5}}{\mathrm{4}}}\right)} ^{\mathrm{0}} \:\left\{\mathrm{2}\left(\mathrm{4}{sh}^{\mathrm{2}} {t}\:+\mathrm{4}{sht}\:+\mathrm{1}\right)−\mathrm{1}\right\}{ch}^{\mathrm{2}} \left({t}\right){dt} \\ $$$$=\mathrm{4}\int_{{ln}\left(\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)} ^{\mathrm{0}} \:\left\{\:\mathrm{8}{sh}^{\mathrm{2}} {t}+\mathrm{8}{sh}\left({t}\right)+\mathrm{1}\right\}{ch}^{\mathrm{2}} {t}\:{dt} \\ $$$$=\mathrm{32}\:\int_{{ln}\left(\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)} ^{\mathrm{0}} \:{sh}^{\mathrm{2}} {t}\:{ch}^{\mathrm{2}} {t}\:{dt}\:+\mathrm{32}\:\int_{{ln}\left(\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)} ^{\mathrm{0}} \:{sh}\left({t}\right){ch}^{\mathrm{2}} \left({t}\right){dt}\:+\mathrm{4}\:\int_{{ln}\left(\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)} ^{\mathrm{0}} {ch}^{\mathrm{2}} \left({t}\right){dt} \\ $$$$\int_{{ln}\left(\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)} ^{\mathrm{0}} \left({shtcht}\right)^{\mathrm{2}} {dt}\:=\frac{\mathrm{1}}{\mathrm{4}}\:\int_{{ln}\left(\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)} ^{\mathrm{0}} {sh}\left(\mathrm{2}{t}\right){dt}\:=\frac{\mathrm{1}}{\mathrm{8}}\left[{ch}\left(\mathrm{2}{t}\right)\right]_{{ln}\left(\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)} ^{\mathrm{0}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{16}}\left[\:{e}^{\mathrm{2}{t}} \:+{e}^{−\mathrm{2}{t}} \right]_{{ln}\left(\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)} ^{\mathrm{0}} \:=\frac{\mathrm{1}}{\mathrm{16}}\left\{\:\mathrm{2}\:−\left(\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\left(\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{2}} }\right\} \\ $$$$\int_{{ln}\left(\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)} ^{\mathrm{0}} \:{sh}\left({t}\right){ch}^{\mathrm{2}} \left({t}\right){dt}\:=\left[\frac{\mathrm{1}}{\mathrm{3}}{ch}^{\mathrm{3}} {t}\right]_{{ln}\left(\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)} ^{\mathrm{0}} \:=\frac{\mathrm{1}}{\mathrm{3}}\left[\:\left(\frac{{e}^{{t}} \:+{e}^{−{t}} }{\mathrm{2}}\right)^{\mathrm{3}} \right]_{{ln}\left(\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)} ^{\mathrm{0}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{24}}\left\{\:\mathrm{8}\:\:−\:\left\{\:\left(\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)−\frac{\mathrm{1}}{\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}}\right\}^{\mathrm{3}} \right\}\:. \\ $$$$\int_{{ln}\left(\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)} ^{\mathrm{0}} \:{ch}^{\mathrm{2}} {t}\:{dt}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{{ln}\left(\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)} ^{\mathrm{0}} \:\left(\mathrm{1}+{ch}\left(\mathrm{2}{t}\right)\right){dt} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)\:+\frac{\mathrm{1}}{\mathrm{4}}\left[{sh}\left(\mathrm{2}{t}\right)\right]_{{ln}\left(\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)} ^{\mathrm{0}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{8}}\left[\:{e}^{\mathrm{2}{t}} −{e}^{−\mathrm{2}{t}} \right]_{{ln}\left(\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)} ^{\mathrm{0}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)\:+\frac{\mathrm{1}}{\mathrm{8}}\left\{−\left(\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{1}}{\left(\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{2}} }\right\} \\ $$$${the}\:{value}\:{of}\:{I}\:{is}\:{known}\:. \\ $$
