Question Number 55994 by maxmathsup by imad last updated on 07/Mar/19
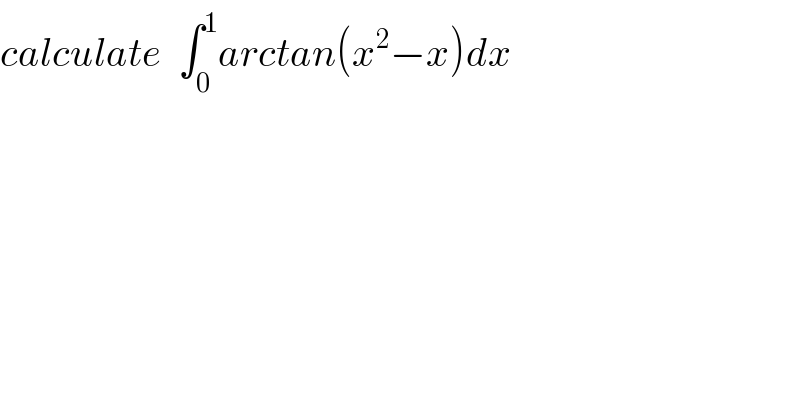
$${calculate}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} {arctan}\left({x}^{\mathrm{2}} −{x}\right){dx} \\ $$
Answered by MJS last updated on 08/Mar/19
![∫arctan (x^2 −x) dx= [t=x^2 −x → dx=(dt/(2x−1))] =∫((arctan t)/( (√(4t+1))))dt= =((√(4t+1))/2)arctan t −(1/2)∫((√(4t+1))/(t^2 +1))dt −(1/2)∫((√(4t+1))/(t^2 +1))dt= [u=(√(4t+1)) → dt=((√(4t+1))/2)du] =−4∫(u^2 /(u^4 −2u^2 +17))du= =−4∫(u^2 /((u^2 −(√(2+2(√(17))))u+(√(17)))(u^2 +(√(2+2(√(17))))u+(√(17)))))du= [a=(√(2+2(√(17)))); b=(√(17))] =−4∫(u^2 /((u^2 −au+b)(u^2 +au+b)))du= =(2/a)(∫(u/(u^2 +au+b))du−∫(u/(u^2 −au+b))du)= =(1/a)ln ((u^2 +au+b)/(u^2 −au+b)) −(2/( (√(4b−a^2 ))))(arctan ((2u−a)/( (√(4b−a^2 )))) +arctan ((2u+a)/( (√(4b−a^2 ))))) ... ∫_0 ^1 arctan (x^2 −x) dx= =((√(−2+2(√(17))))/4)ln ((5+(√(17))+(√(26+10(√(17)))))/8) −((√(2+2(√(17))))/2)arctan ((√(2+2(√(17))))/4) ≈ ≈−.164355](https://www.tinkutara.com/question/Q56008.png)
$$\int\mathrm{arctan}\:\left({x}^{\mathrm{2}} −{x}\right)\:{dx}= \\ $$$$\:\:\:\:\:\left[{t}={x}^{\mathrm{2}} −{x}\:\rightarrow\:{dx}=\frac{{dt}}{\mathrm{2}{x}−\mathrm{1}}\right] \\ $$$$=\int\frac{\mathrm{arctan}\:{t}}{\:\sqrt{\mathrm{4}{t}+\mathrm{1}}}{dt}= \\ $$$$=\frac{\sqrt{\mathrm{4}{t}+\mathrm{1}}}{\mathrm{2}}\mathrm{arctan}\:{t}\:−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\sqrt{\mathrm{4}{t}+\mathrm{1}}}{{t}^{\mathrm{2}} +\mathrm{1}}{dt} \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\sqrt{\mathrm{4}{t}+\mathrm{1}}}{{t}^{\mathrm{2}} +\mathrm{1}}{dt}= \\ $$$$\:\:\:\:\:\left[{u}=\sqrt{\mathrm{4}{t}+\mathrm{1}}\:\rightarrow\:{dt}=\frac{\sqrt{\mathrm{4}{t}+\mathrm{1}}}{\mathrm{2}}{du}\right] \\ $$$$=−\mathrm{4}\int\frac{{u}^{\mathrm{2}} }{{u}^{\mathrm{4}} −\mathrm{2}{u}^{\mathrm{2}} +\mathrm{17}}{du}= \\ $$$$=−\mathrm{4}\int\frac{{u}^{\mathrm{2}} }{\left({u}^{\mathrm{2}} −\sqrt{\mathrm{2}+\mathrm{2}\sqrt{\mathrm{17}}}{u}+\sqrt{\mathrm{17}}\right)\left({u}^{\mathrm{2}} +\sqrt{\mathrm{2}+\mathrm{2}\sqrt{\mathrm{17}}}{u}+\sqrt{\mathrm{17}}\right)}{du}= \\ $$$$\:\:\:\:\:\left[{a}=\sqrt{\mathrm{2}+\mathrm{2}\sqrt{\mathrm{17}}};\:{b}=\sqrt{\mathrm{17}}\right] \\ $$$$=−\mathrm{4}\int\frac{{u}^{\mathrm{2}} }{\left({u}^{\mathrm{2}} −{au}+{b}\right)\left({u}^{\mathrm{2}} +{au}+{b}\right)}{du}= \\ $$$$=\frac{\mathrm{2}}{{a}}\left(\int\frac{{u}}{{u}^{\mathrm{2}} +{au}+{b}}{du}−\int\frac{{u}}{{u}^{\mathrm{2}} −{au}+{b}}{du}\right)= \\ $$$$=\frac{\mathrm{1}}{{a}}\mathrm{ln}\:\frac{{u}^{\mathrm{2}} +{au}+{b}}{{u}^{\mathrm{2}} −{au}+{b}}\:−\frac{\mathrm{2}}{\:\sqrt{\mathrm{4}{b}−{a}^{\mathrm{2}} }}\left(\mathrm{arctan}\:\frac{\mathrm{2}{u}−{a}}{\:\sqrt{\mathrm{4}{b}−{a}^{\mathrm{2}} }}\:+\mathrm{arctan}\:\frac{\mathrm{2}{u}+{a}}{\:\sqrt{\mathrm{4}{b}−{a}^{\mathrm{2}} }}\right) \\ $$$$… \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\mathrm{arctan}\:\left({x}^{\mathrm{2}} −{x}\right)\:{dx}= \\ $$$$=\frac{\sqrt{−\mathrm{2}+\mathrm{2}\sqrt{\mathrm{17}}}}{\mathrm{4}}\mathrm{ln}\:\frac{\mathrm{5}+\sqrt{\mathrm{17}}+\sqrt{\mathrm{26}+\mathrm{10}\sqrt{\mathrm{17}}}}{\mathrm{8}}\:−\frac{\sqrt{\mathrm{2}+\mathrm{2}\sqrt{\mathrm{17}}}}{\mathrm{2}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{2}+\mathrm{2}\sqrt{\mathrm{17}}}}{\mathrm{4}}\:\approx \\ $$$$\approx−.\mathrm{164355} \\ $$
Commented by turbo msup by abdo last updated on 08/Mar/19

$${thanks}\:{sir}. \\ $$
