Question Number 64159 by mathmax by abdo last updated on 14/Jul/19
$${calculate}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dx}}{\mathrm{3}+\mathrm{2}^{{x}} } \\ $$
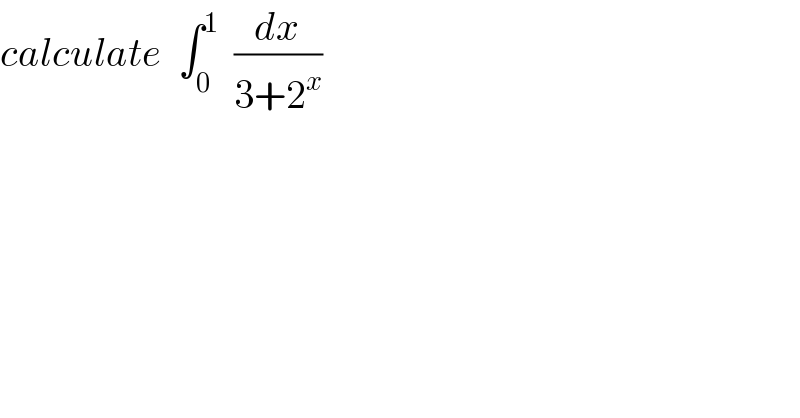
Commented by turbo msup by abdo last updated on 15/Jul/19
![chsngement 2^x =t give e^(xln(2)) =t ⇒ xln(2)=ln(t)⇒x=((ln(t))/(ln2)) ∫_0 ^1 (dx/(3+2^x )) =∫_1 ^2 (dt/(tln2(3+t))) =(1/(3ln2)) ∫_1 ^2 ((1/t)−(1/(3+t)))dt =(1/(3ln2))[ln((t/(t+3)))]_1 ^2 =(1/(3ln2)){ln((2/5))−ln((1/4))} =(1/(3ln2)){ln2−ln5+2ln2} =(1/(3ln2)){3ln2−ln5}](https://www.tinkutara.com/question/Q64215.png)
$${chsngement}\:\mathrm{2}^{{x}} ={t}\:{give}\:{e}^{{xln}\left(\mathrm{2}\right)} ={t}\:\Rightarrow \\ $$$${xln}\left(\mathrm{2}\right)={ln}\left({t}\right)\Rightarrow{x}=\frac{{ln}\left({t}\right)}{{ln}\mathrm{2}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dx}}{\mathrm{3}+\mathrm{2}^{{x}} }\:=\int_{\mathrm{1}} ^{\mathrm{2}} \:\:\frac{{dt}}{{tln}\mathrm{2}\left(\mathrm{3}+{t}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}{ln}\mathrm{2}}\:\int_{\mathrm{1}} ^{\mathrm{2}} \left(\frac{\mathrm{1}}{{t}}−\frac{\mathrm{1}}{\mathrm{3}+{t}}\right){dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}{ln}\mathrm{2}}\left[{ln}\left(\frac{{t}}{{t}+\mathrm{3}}\right)\right]_{\mathrm{1}} ^{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}{ln}\mathrm{2}}\left\{{ln}\left(\frac{\mathrm{2}}{\mathrm{5}}\right)−{ln}\left(\frac{\mathrm{1}}{\mathrm{4}}\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}{ln}\mathrm{2}}\left\{{ln}\mathrm{2}−{ln}\mathrm{5}+\mathrm{2}{ln}\mathrm{2}\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}{ln}\mathrm{2}}\left\{\mathrm{3}{ln}\mathrm{2}−{ln}\mathrm{5}\right\} \\ $$
Answered by Hope last updated on 15/Jul/19
$${f}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{3}+\mathrm{2}^{{x}} } \\ $$$${f}\left(\mathrm{0}\right)=\frac{\mathrm{1}}{\mathrm{4}}=\mathrm{0}.\mathrm{25} \\ $$$${f}\left(\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{5}}=\mathrm{0}.\mathrm{2} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({x}\right){dx}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{0}.\mathrm{25}+\mathrm{0}.\mathrm{20}\right)×\mathrm{1}=\mathrm{0}.\mathrm{225}\left({approx}\right) \\ $$$${Tanmay}\:{is}\:{hope}… \\ $$
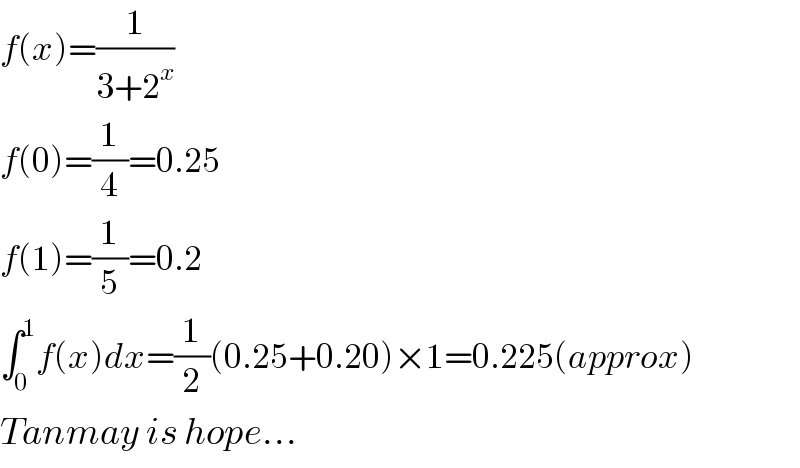
Commented by Hope last updated on 15/Jul/19
$${still}\:{hope}\:{present}..{i}\:{have}\:{changed}\:{my}\:{profile}\:{name} \\ $$$${because}\:{my}\:{answer}\:{do}\:{not}\:{get}\:{accepted}\:{by}\:{a}\left[{few}\right. \\ $$$${so}\:{i}\:{tried}\:{to}\:{minimise}\:\:{my}\:{activity}\:{in}\:{this} \\ $$$${platform}..\mathrm{0}{k}\:{goodbye} \\ $$
Commented by mathmax by abdo last updated on 15/Jul/19
$${sir}\:{tanmay}\:{you}\:{are}\:{wrong}\:{if}\:{you}\:{say}\:{this}\:{what}\:{s}\:{your}\:{proof}\: \\ $$$${that}\:{your}\:{answer}\:{is}\:{not}\:{accepted}\:\:{you}\:{are}\:{always}\:{actif}\:{in}\:{that} \\ $$$${forum}\:{and}\:{considered}…. \\ $$