Question Number 92087 by mathmax by abdo last updated on 04/May/20
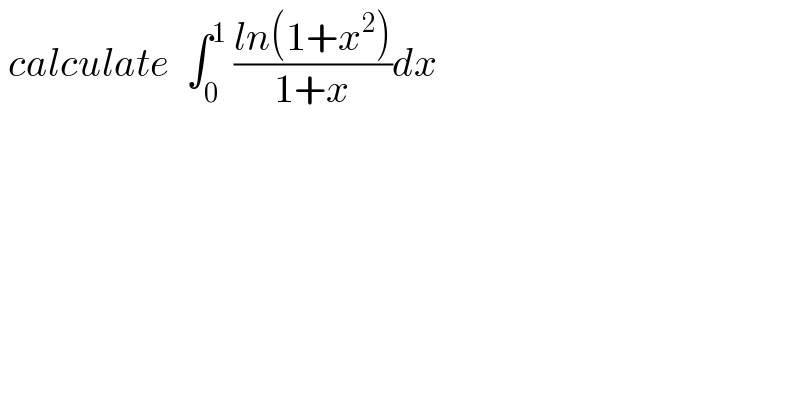
$$\:{calculate}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{\mathrm{1}+{x}}{dx} \\ $$
Commented by mathmax by abdo last updated on 05/May/20
![let f(a) =∫_0 ^1 ((ln(a+x^2 ))/(x+1))dx with a>0 f^′ (a) =∫_0 ^1 (1/((x+1)(x^2 +a)))dx let decompose F(x)=(1/((x+1)(x^2 +a))) F(x) =(α/(x+1)) +((βx +γ)/(x^2 +a)) α =(1/(a+1)) , lim_(x→+∞) xF(x) =0 =α +β ⇒β =−(1/(a+1)) F(x) =(1/((a+1)(x+1))) +((−(1/(a+1))x +γ)/(x^2 +a)) F(0) =(1/a) =(1/(a+1)) +(γ/a) ⇒1 =(a/(a+1)) +γ ⇒ γ =1−(a/(a+1)) =(1/(a+1)) ⇒ F(x) =(1/(a+1)){(1/(x+1)) +((−x +1)/(x^2 +a))} ⇒ ∫_0 ^1 F(x)dx =(1/(a+1)) { ∫_0 ^1 (dx/(x+1))−(1/2)∫_0 ^1 ((2x)/(x^2 +a))dx +∫_0 ^1 (dx/(x^2 +a))} ∫_0 ^1 (dx/(x+1)) =[ln(x+1)]_0 ^1 =ln2 ∫_0 ^1 ((2x)/(x^2 +a))dx =[ln(x^2 +a)]_0 ^1 =ln(1+a)−ln(a) ∫_0 ^1 (dx/(x^2 +a)) =_(x=(√a)t) ∫_0 ^(1/( (√a))) (((√a)dt)/(a(1+t^2 ))) =(1/( (√a)))[arctan(t)]_0 ^(1/( (√a))) =(1/( (√a))){ arctan((1/( (√a))))} ⇒ f^′ (a) =((ln(2))/(a+1))−(1/(2(a+1)))(ln(1+a)−ln(a))+(1/( (√a)(a+1)))arctan((1/( (√a)))) ⇒ f(a) =ln(2) ∫ (da/(a+1)) −(1/2)∫ ((ln(1+a)−ln(a))/(a+1))da + ∫ ((arctan((1/( (√a)))))/( (√a)(a+1)))da +C ∫ (da/(a+1)) =ln(a+1) +c_0 ∫ ((arctan((1/( (√a)))))/( (√a)(a+1)))da =_((√a)=x) ∫ ((arctan((1/x)))/(x(1+x^2 )))(2x)dx =2∫ (((π/2)−arctanx)/(1+x^2 ))dx =π arctan(x)−2 ∫ ((arctanx)/(1+x^2 ))dx but by parts ∫ ((arctanx)/(1+x^2 ))dx =arctan^2 x−∫ ((arctanx)/(1+x^2 ))dx ⇒ ∫((arctanx)/(1+x^2 )) =(1/2) arctan^2 (x)+c_1 ⇒ ∫ ((arctan((1/( (√a)))))/( (√a)(a+1)))da =πarctan((√a))−arctan^2 ((√a)) +c_1 rest to find ∫ ((ln(1+a)−ln(a))/(a+1))da ....be continued....](https://www.tinkutara.com/question/Q92266.png)
$${let}\:{f}\left({a}\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left({a}+{x}^{\mathrm{2}} \right)}{{x}+\mathrm{1}}{dx}\:\:{with}\:{a}>\mathrm{0} \\ $$$${f}^{'} \left({a}\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} \:+{a}\right)}{dx}\:\:{let}\:{decompose}\:{F}\left({x}\right)=\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} \:+{a}\right)} \\ $$$${F}\left({x}\right)\:=\frac{\alpha}{{x}+\mathrm{1}}\:+\frac{\beta{x}\:+\gamma}{{x}^{\mathrm{2}} \:+{a}} \\ $$$$\alpha\:=\frac{\mathrm{1}}{{a}+\mathrm{1}}\:\:,\:\:{lim}_{{x}\rightarrow+\infty} \:{xF}\left({x}\right)\:=\mathrm{0}\:=\alpha\:+\beta\:\Rightarrow\beta\:=−\frac{\mathrm{1}}{{a}+\mathrm{1}} \\ $$$${F}\left({x}\right)\:=\frac{\mathrm{1}}{\left({a}+\mathrm{1}\right)\left({x}+\mathrm{1}\right)}\:+\frac{−\frac{\mathrm{1}}{{a}+\mathrm{1}}{x}\:+\gamma}{{x}^{\mathrm{2}} \:+{a}} \\ $$$${F}\left(\mathrm{0}\right)\:=\frac{\mathrm{1}}{{a}}\:=\frac{\mathrm{1}}{{a}+\mathrm{1}}\:+\frac{\gamma}{{a}}\:\Rightarrow\mathrm{1}\:=\frac{{a}}{{a}+\mathrm{1}}\:+\gamma\:\Rightarrow\:\gamma\:=\mathrm{1}−\frac{{a}}{{a}+\mathrm{1}}\:=\frac{\mathrm{1}}{{a}+\mathrm{1}}\:\Rightarrow \\ $$$${F}\left({x}\right)\:=\frac{\mathrm{1}}{{a}+\mathrm{1}}\left\{\frac{\mathrm{1}}{{x}+\mathrm{1}}\:+\frac{−{x}\:+\mathrm{1}}{{x}^{\mathrm{2}} \:+{a}}\right\}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:{F}\left({x}\right){dx}\:=\frac{\mathrm{1}}{{a}+\mathrm{1}}\:\left\{\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dx}}{{x}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} \:+{a}}{dx}\:+\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dx}}{{x}^{\mathrm{2}} +{a}}\right\} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dx}}{{x}+\mathrm{1}}\:=\left[{ln}\left({x}+\mathrm{1}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:={ln}\mathrm{2} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} \:+{a}}{dx}\:=\left[{ln}\left({x}^{\mathrm{2}} \:+{a}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:={ln}\left(\mathrm{1}+{a}\right)−{ln}\left({a}\right) \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dx}}{{x}^{\mathrm{2}} \:+{a}}\:=_{{x}=\sqrt{{a}}{t}} \:\:\:\:\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\:\sqrt{{a}}}} \:\:\:\:\frac{\sqrt{{a}}{dt}}{{a}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}\:=\frac{\mathrm{1}}{\:\sqrt{{a}}}\left[{arctan}\left({t}\right)\right]_{\mathrm{0}} ^{\frac{\mathrm{1}}{\:\sqrt{{a}}}} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{{a}}}\left\{\:{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{{a}}}\right)\right\}\:\Rightarrow \\ $$$${f}^{'} \left({a}\right)\:=\frac{{ln}\left(\mathrm{2}\right)}{{a}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}\left({a}+\mathrm{1}\right)}\left({ln}\left(\mathrm{1}+{a}\right)−{ln}\left({a}\right)\right)+\frac{\mathrm{1}}{\:\sqrt{{a}}\left({a}+\mathrm{1}\right)}{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{{a}}}\right)\:\Rightarrow \\ $$$${f}\left({a}\right)\:={ln}\left(\mathrm{2}\right)\:\int\:\frac{{da}}{{a}+\mathrm{1}}\:−\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{{ln}\left(\mathrm{1}+{a}\right)−{ln}\left({a}\right)}{{a}+\mathrm{1}}{da} \\ $$$$+\:\int\:\:\frac{{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{{a}}}\right)}{\:\sqrt{{a}}\left({a}+\mathrm{1}\right)}{da}\:+{C} \\ $$$$\int\:\:\frac{{da}}{{a}+\mathrm{1}}\:={ln}\left({a}+\mathrm{1}\right)\:+{c}_{\mathrm{0}} \\ $$$$\int\:\:\frac{{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{{a}}}\right)}{\:\sqrt{{a}}\left({a}+\mathrm{1}\right)}{da}\:=_{\sqrt{{a}}={x}} \:\:\:\:\int\:\:\frac{{arctan}\left(\frac{\mathrm{1}}{{x}}\right)}{{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}\left(\mathrm{2}{x}\right){dx} \\ $$$$=\mathrm{2}\int\:\:\:\frac{\frac{\pi}{\mathrm{2}}−{arctanx}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:=\pi\:{arctan}\left({x}\right)−\mathrm{2}\:\int\:\:\frac{{arctanx}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$${but}\:\:{by}\:{parts}\:\int\:\:\frac{{arctanx}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:={arctan}^{\mathrm{2}} {x}−\int\:\frac{{arctanx}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:\Rightarrow \\ $$$$\int\frac{{arctanx}}{\mathrm{1}+{x}^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{2}}\:{arctan}^{\mathrm{2}} \left({x}\right)+{c}_{\mathrm{1}} \:\Rightarrow \\ $$$$\int\:\:\frac{{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{{a}}}\right)}{\:\sqrt{{a}}\left({a}+\mathrm{1}\right)}{da}\:=\pi{arctan}\left(\sqrt{{a}}\right)−{arctan}^{\mathrm{2}} \left(\sqrt{{a}}\right)\:+{c}_{\mathrm{1}} \\ $$$${rest}\:{to}\:{find}\:\int\:\:\frac{{ln}\left(\mathrm{1}+{a}\right)−{ln}\left({a}\right)}{{a}+\mathrm{1}}{da}\:….{be}\:{continued}…. \\ $$
