Question Number 166437 by mnjuly1970 last updated on 20/Feb/22
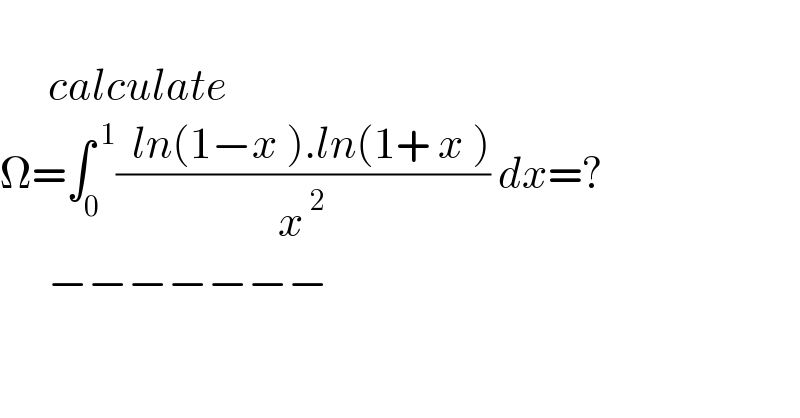
$$ \\ $$$$\:\:\:\:\:\:{calculate}\: \\ $$$$\Omega=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\:\:{ln}\left(\mathrm{1}−{x}\:\right).{ln}\left(\mathrm{1}+\:{x}\:\right)}{{x}^{\:\mathrm{2}} }\:{dx}=? \\ $$$$\:\:\:\:\:\:−−−−−−− \\ $$
Answered by qaz last updated on 21/Feb/22
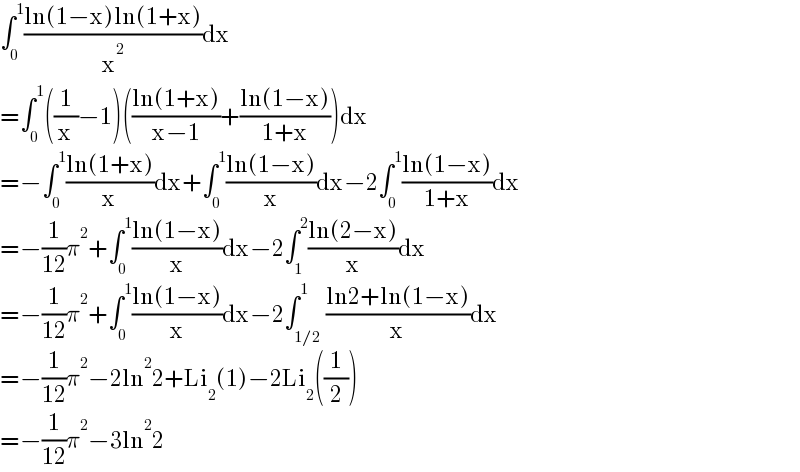
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{x}}−\mathrm{1}\right)\left(\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}−\mathrm{1}}+\frac{\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}}\right)\mathrm{dx} \\ $$$$=−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx}+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx}−\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}}\mathrm{dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{12}}\pi^{\mathrm{2}} +\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx}−\mathrm{2}\int_{\mathrm{1}} ^{\mathrm{2}} \frac{\mathrm{ln}\left(\mathrm{2}−\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{12}}\pi^{\mathrm{2}} +\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx}−\mathrm{2}\int_{\mathrm{1}/\mathrm{2}} ^{\mathrm{1}} \frac{\mathrm{ln2}+\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{12}}\pi^{\mathrm{2}} −\mathrm{2ln}^{\mathrm{2}} \mathrm{2}+\mathrm{Li}_{\mathrm{2}} \left(\mathrm{1}\right)−\mathrm{2Li}_{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$=−\frac{\mathrm{1}}{\mathrm{12}}\pi^{\mathrm{2}} −\mathrm{3ln}^{\mathrm{2}} \mathrm{2} \\ $$
