Question Number 36180 by prof Abdo imad last updated on 30/May/18
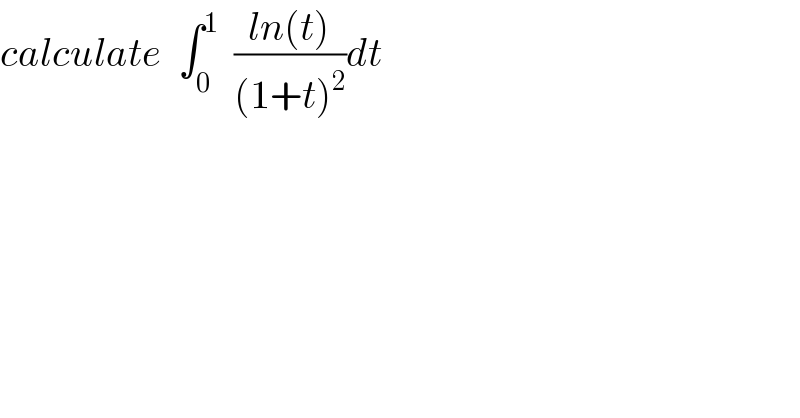
$${calculate}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{ln}\left({t}\right)}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }{dt} \\ $$
Commented by prof Abdo imad last updated on 30/May/18
![let put I = ∫_0 ^1 ((ln(t))/((1+t)^2 ))dt let integrate by parts I =[(1−(1/(1+t)))ln(t)]_0 ^1 −∫_0 ^1 (1−(1/(1+t)))(dt/t) =0 − ∫_0 ^1 (dt/(1+t)) =−[ln∣1+t∣]_0 ^1 =−ln(2) let prove that lim_(t→0) (1−(1/(1+t)))ln(t)=0 lim_(t→0) (1−(1/(1+t)))ln(t) =lim_(t→0) ((tln(t))/(1+t)) =0 because lim_(t→0) tln(t) =0 so ★ ∫_0 ^1 ((ln(t))/((1+t)^2 ))dt =−ln(2)★](https://www.tinkutara.com/question/Q36261.png)
$${let}\:{put}\:{I}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{ln}\left({t}\right)}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }{dt}\:\:{let}\:{integrate}\:{by}\:{parts} \\ $$$${I}\:\:=\left[\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+{t}}\right){ln}\left({t}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+{t}}\right)\frac{{dt}}{{t}} \\ $$$$=\mathrm{0}\:−\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dt}}{\mathrm{1}+{t}}\:=−\left[{ln}\mid\mathrm{1}+{t}\mid\right]_{\mathrm{0}} ^{\mathrm{1}} \:=−{ln}\left(\mathrm{2}\right) \\ $$$${let}\:{prove}\:{that}\:{lim}_{{t}\rightarrow\mathrm{0}} \left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+{t}}\right){ln}\left({t}\right)=\mathrm{0} \\ $$$${lim}_{{t}\rightarrow\mathrm{0}} \left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+{t}}\right){ln}\left({t}\right)\:={lim}_{{t}\rightarrow\mathrm{0}} \frac{{tln}\left({t}\right)}{\mathrm{1}+{t}}\:=\mathrm{0} \\ $$$${because}\:\:{lim}_{{t}\rightarrow\mathrm{0}} {tln}\left({t}\right)\:=\mathrm{0}\:{so} \\ $$$$\bigstar\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{ln}\left({t}\right)}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }{dt}\:=−{ln}\left(\mathrm{2}\right)\bigstar \\ $$
Answered by sma3l2996 last updated on 30/May/18
![I=∫_0 ^1 ((lnt)/((1+t)^2 ))dt by parts u=lnt⇒u′=(1/t) v′=(1/((1+t)^2 ))⇒v=−(1/(1+t)) I=[−((lnt)/(1+t))]_0 ^1 +∫_0 ^1 (dt/(t(1+t))) =lim_(t→0^+ ) ((lnt)/(1+t))+∫_0 ^1 ((1/t)−(1/(1+t)))dt =lim_(t→0^+ ) ((lnt)/(1+t))+[ln((t/(1+t)))]_0 ^1 =lim_(t→0^+ ) (((lnt)/(1+t))−ln(t))−ln2 =−lim_(x→0^+ ) ((tln(t))/(1+t))−ln2=−ln2 (because lim_(x→0^+ ) xlnx=0)](https://www.tinkutara.com/question/Q36199.png)
$${I}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{lnt}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }{dt} \\ $$$${by}\:{parts}\: \\ $$$${u}={lnt}\Rightarrow{u}'=\frac{\mathrm{1}}{{t}} \\ $$$${v}'=\frac{\mathrm{1}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }\Rightarrow{v}=−\frac{\mathrm{1}}{\mathrm{1}+{t}} \\ $$$${I}=\left[−\frac{{lnt}}{\mathrm{1}+{t}}\right]_{\mathrm{0}} ^{\mathrm{1}} +\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dt}}{{t}\left(\mathrm{1}+{t}\right)} \\ $$$$=\underset{{t}\rightarrow\mathrm{0}^{+} } {{lim}}\frac{{lnt}}{\mathrm{1}+{t}}+\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{\mathrm{1}}{{t}}−\frac{\mathrm{1}}{\mathrm{1}+{t}}\right){dt} \\ $$$$=\underset{{t}\rightarrow\mathrm{0}^{+} } {{lim}}\frac{{lnt}}{\mathrm{1}+{t}}+\left[{ln}\left(\frac{{t}}{\mathrm{1}+{t}}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\underset{{t}\rightarrow\mathrm{0}^{+} } {{lim}}\left(\frac{{lnt}}{\mathrm{1}+{t}}−{ln}\left({t}\right)\right)−{ln}\mathrm{2} \\ $$$$=−\underset{{x}\rightarrow\mathrm{0}^{+} } {{lim}}\frac{{tln}\left({t}\right)}{\mathrm{1}+{t}}−{ln}\mathrm{2}=−{ln}\mathrm{2}\:\:\:\left({because}\:\:\underset{{x}\rightarrow\mathrm{0}^{+} } {{lim}xlnx}=\mathrm{0}\right) \\ $$$$ \\ $$
