Question Number 98444 by mathmax by abdo last updated on 14/Jun/20
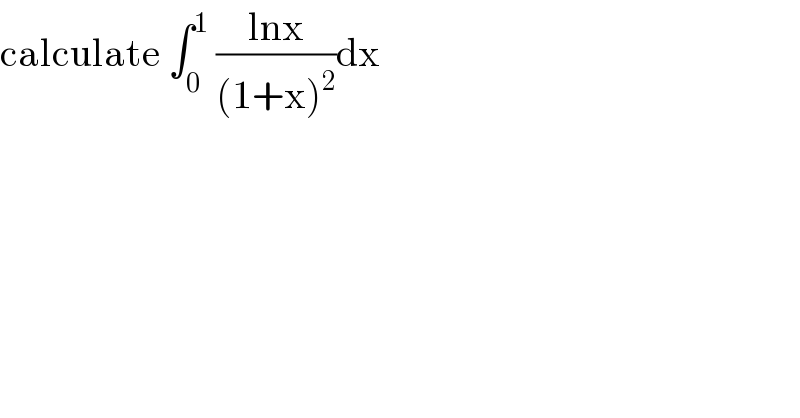
$$\mathrm{calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{lnx}}{\left(\mathrm{1}+\mathrm{x}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$
Answered by abdomathmax last updated on 14/Jun/20
![I =∫_0 ^1 ((lnx)/((1+x)^2 ))dx by parts u^′ =(1/((1+x)^2 )) and v=lnx I =[(1−(1/(1+x)))lnx]_0 ^1 −∫_0 ^1 (1−(1/(1+x)))(dx/x) =[((xlnx)/(1+x))]_0 ^1 −∫_0 ^1 ((xdx)/(x(1+x))) =0−∫_0 ^1 (dx/(1+x)) =−[ln(1+x)]_0 ^1 =−ln(2) ⇒ ∫_0 ^1 ((lnx)/((1+x)^2 ))dx =−ln(2)](https://www.tinkutara.com/question/Q98518.png)
$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{lnx}}{\left(\mathrm{1}+\mathrm{x}\right)^{\mathrm{2}} }\mathrm{dx}\:\mathrm{by}\:\mathrm{parts}\:\mathrm{u}^{'} \:=\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{x}\right)^{\mathrm{2}} }\:\mathrm{and}\:\mathrm{v}=\mathrm{lnx} \\ $$$$\mathrm{I}\:=\left[\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}}\right)\mathrm{lnx}\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}}\right)\frac{\mathrm{dx}}{\mathrm{x}} \\ $$$$=\left[\frac{\mathrm{xlnx}}{\mathrm{1}+\mathrm{x}}\right]_{\mathrm{0}} ^{\mathrm{1}} \:−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{xdx}}{\mathrm{x}\left(\mathrm{1}+\mathrm{x}\right)}\:=\mathrm{0}−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{x}} \\ $$$$=−\left[\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:=−\mathrm{ln}\left(\mathrm{2}\right)\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{lnx}}{\left(\mathrm{1}+\mathrm{x}\right)^{\mathrm{2}} }\mathrm{dx}\:=−\mathrm{ln}\left(\mathrm{2}\right) \\ $$
