Question Number 51186 by Abdo msup. last updated on 24/Dec/18
![calculate ∫_0 ^1 (([nx])/(2x+1))dx](https://www.tinkutara.com/question/Q51186.png)
$${calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\left[{nx}\right]}{\mathrm{2}{x}+\mathrm{1}}{dx} \\ $$
Commented by Abdo msup. last updated on 25/Dec/18
![let A_n =∫_0 ^1 (([nx])/(2x+1))dx ⇒A_n =Σ_(k=0) ^(n−1) ∫_(k/n) ^((k+1)/n) (k/(2x+1)) ([nx]=k) ⇒A_n =(1/2) Σ_(k=0) ^(n−1) k [ln(2x+1)]_(k/n) ^((k+1)/n) =(1/2) Σ_(k=0) ^(n−1) k {ln(((2(k+1))/n)+1)−ln(((2k)/n)+1)} =(1/2)Σ_(k=0) ^(n−1) k{ ln(2k+n+2)+ln(2k+n)} =(1/2)Σ_(k=0) ^(n−1) k ln(((2k+n +2)/(2k+n))) ⇒ A_n =(1/2){ln(((n+4)/(n+3)))+2ln(((n+6)/(n+4)))+3ln(((n+8)/(n+6)))+... +(n−1)ln(((3n)/(3n−2)))}](https://www.tinkutara.com/question/Q51290.png)
$${let}\:{A}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\left[{nx}\right]}{\mathrm{2}{x}+\mathrm{1}}{dx}\:\Rightarrow{A}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\int_{\frac{{k}}{{n}}} ^{\frac{{k}+\mathrm{1}}{{n}}} \:\:\:\frac{{k}}{\mathrm{2}{x}+\mathrm{1}} \\ $$$$\left(\left[{nx}\right]={k}\right)\:\Rightarrow{A}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}\:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:{k}\:\left[{ln}\left(\mathrm{2}{x}+\mathrm{1}\right)\right]_{\frac{{k}}{{n}}} ^{\frac{{k}+\mathrm{1}}{{n}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:{k}\:\left\{{ln}\left(\frac{\mathrm{2}\left({k}+\mathrm{1}\right)}{{n}}+\mathrm{1}\right)−{ln}\left(\frac{\mathrm{2}{k}}{{n}}+\mathrm{1}\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} {k}\left\{\:{ln}\left(\mathrm{2}{k}+{n}+\mathrm{2}\right)+{ln}\left(\mathrm{2}{k}+{n}\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:{k}\:{ln}\left(\frac{\mathrm{2}{k}+{n}\:+\mathrm{2}}{\mathrm{2}{k}+{n}}\right)\:\Rightarrow \\ $$$${A}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}\left\{{ln}\left(\frac{{n}+\mathrm{4}}{{n}+\mathrm{3}}\right)+\mathrm{2}{ln}\left(\frac{{n}+\mathrm{6}}{{n}+\mathrm{4}}\right)+\mathrm{3}{ln}\left(\frac{{n}+\mathrm{8}}{{n}+\mathrm{6}}\right)+…\right. \\ $$$$\left.+\left({n}−\mathrm{1}\right){ln}\left(\frac{\mathrm{3}{n}}{\mathrm{3}{n}−\mathrm{2}}\right)\right\} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 24/Dec/18
![∫_0 ^(1/n) (([nx])/(2(x+(1/2))))dx+∫_(1/n) ^1 (([nx])/(2(x+(1/2))))dx ∫_0 ^(1/n) (0/(2(x+(1/2))))dx+∫_(1/n) ^1 (1/(2(x+(1/2))))dx (1/2)∣ln(x+(1/2))∣_(1/n) ^1 =(1/2){ln((3/2))−ln((1/n)+(1/2))} =(1/2)ln(((3/2)/((2+n)/(2n)))) (1/2)ln(((3×2n)/(2(2+n)))) =(1/2)ln(((3n)/(2+n)))](https://www.tinkutara.com/question/Q51192.png)
$$\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{{n}}} \frac{\left[{nx}\right]}{\mathrm{2}\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)}{dx}+\int_{\frac{\mathrm{1}}{{n}}} ^{\mathrm{1}} \:\frac{\left[{nx}\right]}{\mathrm{2}\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)}{dx} \\ $$$$\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{{n}}} \frac{\mathrm{0}}{\mathrm{2}\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)}{dx}+\int_{\frac{\mathrm{1}}{{n}}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\mid{ln}\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)\mid_{\frac{\mathrm{1}}{{n}}} ^{\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{{ln}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)−{ln}\left(\frac{\mathrm{1}}{{n}}+\frac{\mathrm{1}}{\mathrm{2}}\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{\frac{\mathrm{3}}{\mathrm{2}}}{\frac{\mathrm{2}+{n}}{\mathrm{2}{n}}}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{\mathrm{3}×\mathrm{2}{n}}{\mathrm{2}\left(\mathrm{2}+{n}\right)}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{\mathrm{3}{n}}{\mathrm{2}+{n}}\right) \\ $$$$ \\ $$
Commented by Abdo msup. last updated on 25/Dec/18
![sir Tanmay if (1/n)≤x≤1 ⇒1≤nx≤n so [nx] is not equal to 1!!](https://www.tinkutara.com/question/Q51212.png)
$${sir}\:{Tanmay}\:\:{if}\:\:\frac{\mathrm{1}}{{n}}\leqslant{x}\leqslant\mathrm{1}\:\:\Rightarrow\mathrm{1}\leqslant{nx}\leqslant{n}\:\:{so}\:\left[{nx}\right]\:{is} \\ $$$${not}\:{equal}\:{to}\:\mathrm{1}!! \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 25/Dec/18
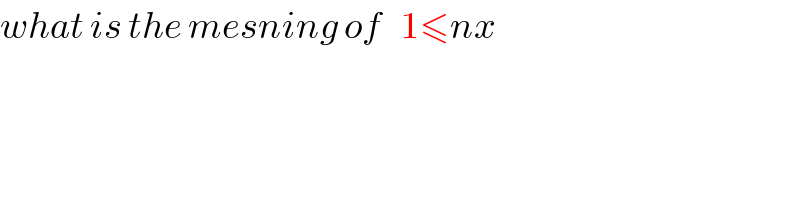
$${what}\:{is}\:{the}\:{mesning}\:{of}\:\:\:\mathrm{1}\leqslant{nx}\:\: \\ $$
