Question Number 53782 by maxmathsup by imad last updated on 25/Jan/19
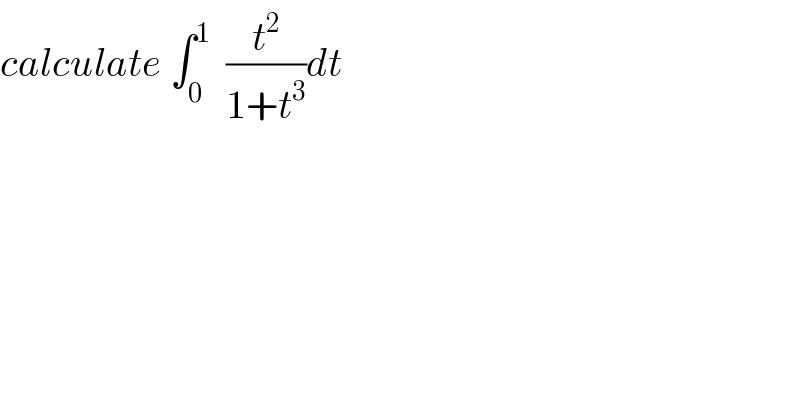
$${calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{3}} }{dt} \\ $$
Answered by Smail last updated on 26/Jan/19
![∫_0 ^1 (t^2 /(1+t^3 ))dt=(1/3)∫_0 ^1 ((d(1+t^3 ))/(1+t^3 ))=(1/3)[ln∣1+t^3 ∣]_0 ^1 =((ln2)/3)](https://www.tinkutara.com/question/Q53797.png)
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{3}} }{dt}=\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{d}\left(\mathrm{1}+{t}^{\mathrm{3}} \right)}{\mathrm{1}+{t}^{\mathrm{3}} }=\frac{\mathrm{1}}{\mathrm{3}}\left[{ln}\mid\mathrm{1}+{t}^{\mathrm{3}} \mid\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{{ln}\mathrm{2}}{\mathrm{3}} \\ $$
