Question Number 36431 by prof Abdo imad last updated on 02/Jun/18
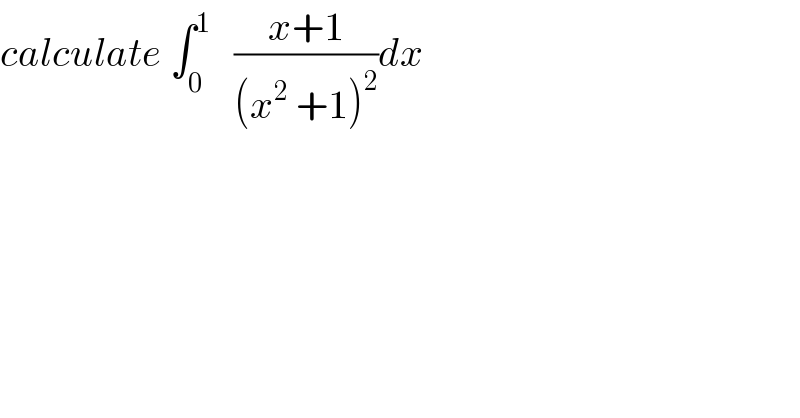
$${calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{x}+\mathrm{1}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$
Commented by prof Abdo imad last updated on 03/Jun/18
![I = (1/2)∫_0 ^1 ((2x +2)/((x^2 +1)^2 ))dx =(1/2)∫ ((2x)/((x^2 +1)^2 )) + ∫_0 ^1 (dx/((x^2 +1)^2 )) =[((−1)/(2(x^2 +1)))]_0 ^1 + ∫_0 ^1 (dx/((x^2 +1)^2 )) changement x=tanθ give ∫_0 ^1 (dx/((1+x^2 )^2 )) = ∫_0 ^(π/4) (((1+tan^2 θ))/((1+tan^2 θ)^2 ))dθ = ∫_0 ^(π/4) cos^2 θ dθ = ∫_0 ^(π/4) ((1+cos(2θ))/2)dθ =(π/8) +(1/4)[sin(2θ)]_0 ^(π/4) = (π/8) + (1/4) ⇒ I =(1/2) −(1/4) +(π/8) +(1/4) ⇒ I = (π/8) +(1/2) .](https://www.tinkutara.com/question/Q36672.png)
$${I}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{2}{x}\:+\mathrm{2}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }{dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\frac{\mathrm{2}{x}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:+\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dx}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\left[\frac{−\mathrm{1}}{\mathrm{2}\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)}\right]_{\mathrm{0}} ^{\mathrm{1}} \:+\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:\:{changement} \\ $$$${x}={tan}\theta\:{give}\: \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\frac{{dx}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\:\frac{\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right)}{\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right)^{\mathrm{2}} }{d}\theta \\ $$$$=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:{cos}^{\mathrm{2}} \theta\:{d}\theta\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{\mathrm{1}+{cos}\left(\mathrm{2}\theta\right)}{\mathrm{2}}{d}\theta \\ $$$$=\frac{\pi}{\mathrm{8}}\:\:+\frac{\mathrm{1}}{\mathrm{4}}\left[{sin}\left(\mathrm{2}\theta\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:=\:\frac{\pi}{\mathrm{8}}\:+\:\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow \\ $$$${I}\:=\frac{\mathrm{1}}{\mathrm{2}}\:−\frac{\mathrm{1}}{\mathrm{4}}\:+\frac{\pi}{\mathrm{8}}\:+\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow \\ $$$$\:{I}\:=\:\frac{\pi}{\mathrm{8}}\:+\frac{\mathrm{1}}{\mathrm{2}}\:. \\ $$
