Menu Close

calculate-0-1-x-2-1-ln-x-x-2-2x-1-x-2-2x-1-dx-

Tinku Tara 0 Comments
Pin




Question Number 47114 by maxmathsup by imad last updated on 04/Nov/18
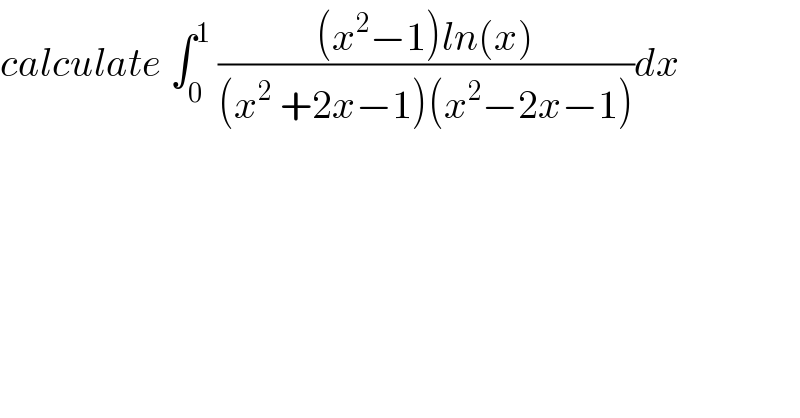
calculate ∫_0 ^1 (((x^2 −1)ln(x))/((x^2 +2x−1)(x^2 −2x−1)))dx
$${calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\left({x}^{\mathrm{2}} −\mathrm{1}\right){ln}\left({x}\right)}{\left({x}^{\mathrm{2}} \:+\mathrm{2}{x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{1}\right)}{dx} \\ $$
Commented by maxmathsup by imad last updated on 11/Nov/18
let decompose F(x)=((x^2 −1)/((x^2 +2x−1)(x^2 −2x−1))) ⇒F(x)=((x^2 −1)/((x^2 +2x+1−2)(x^2 −2x+1 −2))) =((x^2 −1)/(((x+1)^2 −2)((x−1)^2 −2))) =((x^2 −1)/((x+1−(√2))(x+1+(√2))(x−1−(√2))(x−1+(√2)))) =((x^2 −1)/((x−x_1 )(x−x_2 )(x−t_1 )(x−t_2 ))) with x_1 =−1+(√2), x_2 =−1−(√2), t_1 =1+(√2) and t_2 =1−(√2) F(x)=(a/(x−x_1 )) +(b/(x−x_2 )) +(c/(x−t_1 )) +(d/(x−t_2 )) a =lim_(x→x_(1 ) ) (x−x_1 )F(x)=((x_(1 ) ^2 −1)/((x_1 −x_2 )(x_1 −t_1 )(x_1 −t_2 ))) =((2−2(√2))/(2(√2)(−2)(−2+2(√2)))) =((−1)/(−4(√2))) =(1/(4(√2))) . b =lim_(x→x_2 ) (x−x_2 )F(x) = ((x_(2 ) ^2 −1)/((x_2 −x_1 )(x_2 −t_1 )(x_2 −t_2 ))) =((2+2(√2))/(−2(√2))(−2−2(√2))(−2))) =−(1/(4(√2))) c =lim_(x→t_1 ) (x−t_1 )F(x) =((t_1 ^2 −1)/((t_1 −x_1 )(t_1 −x_2 )(t_1 −t_2 ))) =((2+2(√2))/(2(2+2(√2))2(√2))) =(1/(4(√2))) d =lim_(x→t_2 ) (x−t_2 )F(t) = ((t_2 ^2 −1)/((t_2 −x_1 )(t_2 −x_2 )(t_2 −t_1 ))) =((2−2(√2))/(2−2(√2))(2)(−2(√2)))) =−(1/(4(√2))) ⇒ F(x) = (1/(4(√2))){ (1/(x−x_1 )) −(1/(x−x_2 )) +(1/(x−t_1 )) −(1/(x−t_2 ))} ⇒ I =∫_0 ^1 ln(x)F(x)dx =(1/(4(√2))) {∫_0 ^1 ((ln(x)dx)/(x−x_1 )) −∫_0 ^1 ((ln(x))/(x−x_2 ))dx +∫_0 ^1 ((ln(x))/(x−t_1 ))dx−∫_0 ^1 ((ln(x))/(x−t_2 ))dx} let determine ∫_0 ^1 ((ln(x))/(x−x_1 ))dx....be continued....
$${let}\:{decompose}\:{F}\left({x}\right)=\frac{{x}^{\mathrm{2}} −\mathrm{1}}{\left({x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{1}\right)} \\ $$$$\Rightarrow{F}\left({x}\right)=\frac{{x}^{\mathrm{2}} −\mathrm{1}}{\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{1}−\mathrm{2}\right)\left({x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}\:−\mathrm{2}\right)}\:=\frac{{x}^{\mathrm{2}} −\mathrm{1}}{\left(\left({x}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}\right)\left(\left({x}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}\right)} \\ $$$$=\frac{{x}^{\mathrm{2}} −\mathrm{1}}{\left({x}+\mathrm{1}−\sqrt{\mathrm{2}}\right)\left({x}+\mathrm{1}+\sqrt{\mathrm{2}}\right)\left({x}−\mathrm{1}−\sqrt{\mathrm{2}}\right)\left({x}−\mathrm{1}+\sqrt{\mathrm{2}}\right)}\:=\frac{{x}^{\mathrm{2}} −\mathrm{1}}{\left({x}−{x}_{\mathrm{1}} \right)\left({x}−{x}_{\mathrm{2}} \right)\left({x}−{t}_{\mathrm{1}} \right)\left({x}−{t}_{\mathrm{2}} \right)} \\ $$$${with}\:{x}_{\mathrm{1}} =−\mathrm{1}+\sqrt{\mathrm{2}},\:\:{x}_{\mathrm{2}} =−\mathrm{1}−\sqrt{\mathrm{2}},\:\:{t}_{\mathrm{1}} =\mathrm{1}+\sqrt{\mathrm{2}}\:\:\:{and}\:{t}_{\mathrm{2}} =\mathrm{1}−\sqrt{\mathrm{2}} \\ $$$${F}\left({x}\right)=\frac{{a}}{{x}−{x}_{\mathrm{1}} }\:+\frac{{b}}{{x}−{x}_{\mathrm{2}} }\:+\frac{{c}}{{x}−{t}_{\mathrm{1}} }\:+\frac{{d}}{{x}−{t}_{\mathrm{2}} } \\ $$$${a}\:={lim}_{{x}\rightarrow{x}_{\mathrm{1}\:} } \:\:\:\left({x}−{x}_{\mathrm{1}} \right){F}\left({x}\right)=\frac{{x}_{\mathrm{1}\:} ^{\mathrm{2}} −\mathrm{1}}{\left({x}_{\mathrm{1}} −{x}_{\mathrm{2}} \right)\left({x}_{\mathrm{1}} −{t}_{\mathrm{1}} \right)\left({x}_{\mathrm{1}} −{t}_{\mathrm{2}} \right)} \\ $$$$=\frac{\mathrm{2}−\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{2}\sqrt{\mathrm{2}}\left(−\mathrm{2}\right)\left(−\mathrm{2}+\mathrm{2}\sqrt{\mathrm{2}}\right)}\:=\frac{−\mathrm{1}}{−\mathrm{4}\sqrt{\mathrm{2}}}\:=\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}\:. \\ $$$${b}\:={lim}_{{x}\rightarrow{x}_{\mathrm{2}} \:} \:\:\:\left({x}−{x}_{\mathrm{2}} \right){F}\left({x}\right)\:=\:\frac{{x}_{\mathrm{2}\:} ^{\mathrm{2}} −\mathrm{1}}{\left({x}_{\mathrm{2}} −{x}_{\mathrm{1}} \right)\left({x}_{\mathrm{2}} −{t}_{\mathrm{1}} \right)\left({x}_{\mathrm{2}} −{t}_{\mathrm{2}} \right)} \\ $$$$=\frac{\mathrm{2}+\mathrm{2}\sqrt{\mathrm{2}}}{\left.−\mathrm{2}\sqrt{\mathrm{2}}\right)\left(−\mathrm{2}−\mathrm{2}\sqrt{\mathrm{2}}\right)\left(−\mathrm{2}\right)}\:=−\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}} \\ $$$${c}\:={lim}_{{x}\rightarrow{t}_{\mathrm{1}} } \left({x}−{t}_{\mathrm{1}} \right){F}\left({x}\right)\:=\frac{{t}_{\mathrm{1}} ^{\mathrm{2}} −\mathrm{1}}{\left({t}_{\mathrm{1}} −{x}_{\mathrm{1}} \right)\left({t}_{\mathrm{1}} −{x}_{\mathrm{2}} \right)\left({t}_{\mathrm{1}} −{t}_{\mathrm{2}} \right)} \\ $$$$=\frac{\mathrm{2}+\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{2}\left(\mathrm{2}+\mathrm{2}\sqrt{\mathrm{2}}\right)\mathrm{2}\sqrt{\mathrm{2}}}\:=\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}} \\ $$$${d}\:={lim}_{{x}\rightarrow{t}_{\mathrm{2}} } \left({x}−{t}_{\mathrm{2}} \right){F}\left({t}\right)\:=\:\frac{{t}_{\mathrm{2}} ^{\mathrm{2}} −\mathrm{1}}{\left({t}_{\mathrm{2}} −{x}_{\mathrm{1}} \right)\left({t}_{\mathrm{2}} −{x}_{\mathrm{2}} \right)\left({t}_{\mathrm{2}} −{t}_{\mathrm{1}} \right)} \\ $$$$=\frac{\mathrm{2}−\mathrm{2}\sqrt{\mathrm{2}}}{\left.\mathrm{2}−\mathrm{2}\sqrt{\mathrm{2}}\right)\left(\mathrm{2}\right)\left(−\mathrm{2}\sqrt{\mathrm{2}}\right)}\:=−\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}\:\Rightarrow \\ $$$${F}\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}\left\{\:\frac{\mathrm{1}}{{x}−{x}_{\mathrm{1}} }\:−\frac{\mathrm{1}}{{x}−{x}_{\mathrm{2}} }\:+\frac{\mathrm{1}}{{x}−{t}_{\mathrm{1}} }\:−\frac{\mathrm{1}}{{x}−{t}_{\mathrm{2}} }\right\}\:\Rightarrow \\ $$$${I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:{ln}\left({x}\right){F}\left({x}\right){dx}\:=\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{2}}}\:\left\{\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{ln}\left({x}\right){dx}}{{x}−{x}_{\mathrm{1}} }\:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left({x}\right)}{{x}−{x}_{\mathrm{2}} }{dx}\:+\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left({x}\right)}{{x}−{t}_{\mathrm{1}} }{dx}−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left({x}\right)}{{x}−{t}_{\mathrm{2}} }{dx}\right\} \\ $$$${let}\:{determine}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{ln}\left({x}\right)}{{x}−{x}_{\mathrm{1}} }{dx}….{be}\:{continued}…. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *