Menu Close

calculate-0-1-xe-x-2-arctan-2-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 99824 by mathmax by abdo last updated on 23/Jun/20
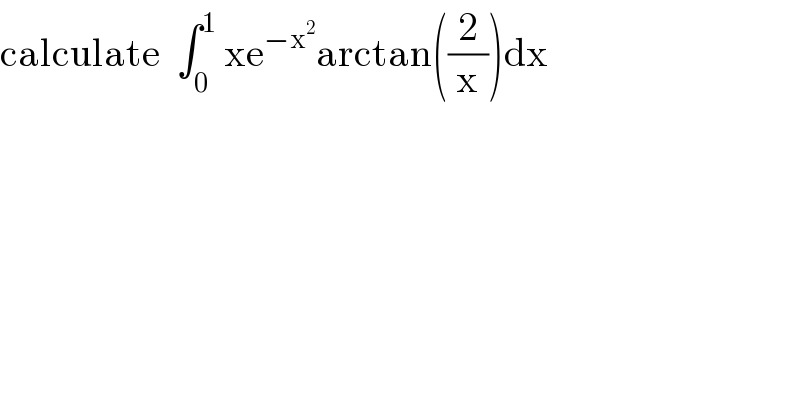
calculate ∫_0 ^1 xe^(−x^2 ) arctan((2/x))dx
$$\mathrm{calculate}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{xe}^{−\mathrm{x}^{\mathrm{2}} } \mathrm{arctan}\left(\frac{\mathrm{2}}{\mathrm{x}}\right)\mathrm{dx} \\ $$
Answered by maths mind last updated on 23/Jun/20
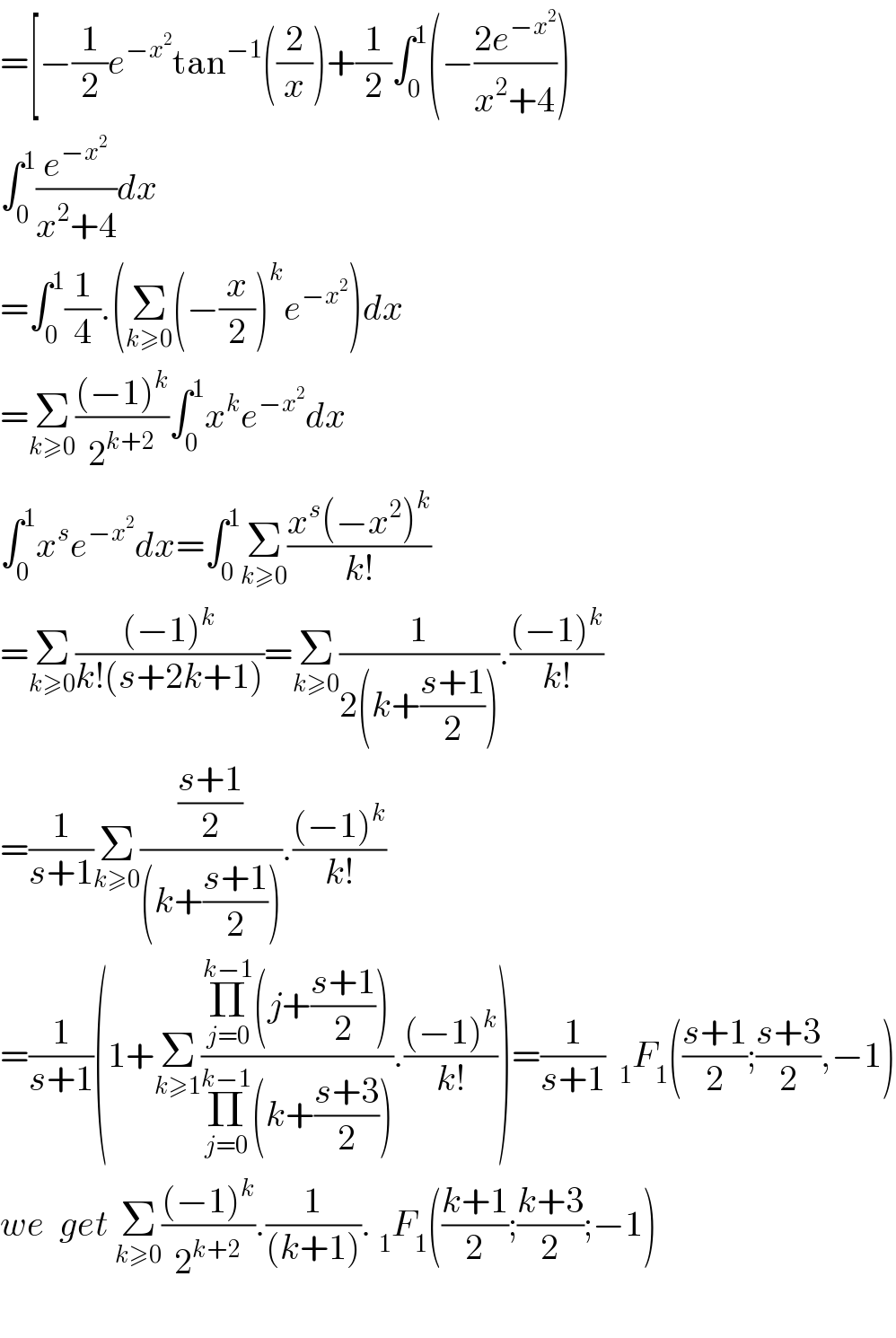
=[−(1/2)e^(−x^2 ) tan^(−1) ((2/x))+(1/2)∫_0 ^1 (−((2e^(−x^2 ) )/(x^2 +4))) ∫_0 ^1 (e^(−x^2 ) /(x^2 +4))dx =∫_0 ^1 (1/4).(Σ_(k≥0) (−(x/2))^k e^(−x^2 ) )dx =Σ_(k≥0) (((−1)^k )/2^(k+2) )∫_0 ^1 x^k e^(−x^2 ) dx ∫_0 ^1 x^s e^(−x^2 ) dx=∫_0 ^1 Σ_(k≥0) ((x^s (−x^2 )^k )/(k!)) =Σ_(k≥0) (((−1)^k )/(k!(s+2k+1)))=Σ_(k≥0) (1/(2(k+((s+1)/2)))).(((−1)^k )/(k!)) =(1/(s+1))Σ_(k≥0) (((s+1)/2)/((k+((s+1)/2)))).(((−1)^k )/(k!)) =(1/(s+1))(1+Σ_(k≥1) ((Π_(j=0) ^(k−1) (j+((s+1)/2)))/(Π_(j=0) ^(k−1) (k+((s+3)/2)))).(((−1)^k )/(k!)))=(1/(s+1)) _1 F_1 (((s+1)/2);((s+3)/2),−1) we get Σ_(k≥0) (((−1)^k )/2^(k+2) ).(1/((k+1))). _1 F_1 (((k+1)/2);((k+3)/2);−1)
$$=\left[−\frac{\mathrm{1}}{\mathrm{2}}{e}^{−{x}^{\mathrm{2}} } \mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}}{{x}}\right)+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \left(−\frac{\mathrm{2}{e}^{−{x}^{\mathrm{2}} } }{{x}^{\mathrm{2}} +\mathrm{4}}\right)\right. \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{e}^{−{x}^{\mathrm{2}} } }{{x}^{\mathrm{2}} +\mathrm{4}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{4}}.\left(\underset{{k}\geqslant\mathrm{0}} {\sum}\left(−\frac{{x}}{\mathrm{2}}\right)^{{k}} {e}^{−{x}^{\mathrm{2}} } \right){dx} \\ $$$$=\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}} }{\mathrm{2}^{{k}+\mathrm{2}} }\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{k}} {e}^{−{x}^{\mathrm{2}} } {dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{s}} {e}^{−{x}^{\mathrm{2}} } {dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \underset{{k}\geqslant\mathrm{0}} {\sum}\frac{{x}^{{s}} \left(−{x}^{\mathrm{2}} \right)^{{k}} }{{k}!} \\ $$$$=\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}!\left({s}+\mathrm{2}{k}+\mathrm{1}\right)}=\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{\mathrm{2}\left({k}+\frac{{s}+\mathrm{1}}{\mathrm{2}}\right)}.\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}!} \\ $$$$=\frac{\mathrm{1}}{{s}+\mathrm{1}}\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\frac{{s}+\mathrm{1}}{\mathrm{2}}}{\left({k}+\frac{{s}+\mathrm{1}}{\mathrm{2}}\right)}.\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}!} \\ $$$$=\frac{\mathrm{1}}{{s}+\mathrm{1}}\left(\mathrm{1}+\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{\underset{{j}=\mathrm{0}} {\overset{{k}−\mathrm{1}} {\prod}}\left({j}+\frac{{s}+\mathrm{1}}{\mathrm{2}}\right)}{\underset{{j}=\mathrm{0}} {\overset{{k}−\mathrm{1}} {\prod}}\left({k}+\frac{{s}+\mathrm{3}}{\mathrm{2}}\right)}.\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}!}\right)=\frac{\mathrm{1}}{{s}+\mathrm{1}}\:\:_{\mathrm{1}} {F}_{\mathrm{1}} \left(\frac{{s}+\mathrm{1}}{\mathrm{2}};\frac{{s}+\mathrm{3}}{\mathrm{2}},−\mathrm{1}\right) \\ $$$${we}\:\:{get}\:\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}} }{\mathrm{2}^{{k}+\mathrm{2}} }.\frac{\mathrm{1}}{\left({k}+\mathrm{1}\right)}.\:_{\mathrm{1}} {F}_{\mathrm{1}} \left(\frac{{k}+\mathrm{1}}{\mathrm{2}};\frac{{k}+\mathrm{3}}{\mathrm{2}};−\mathrm{1}\right) \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 23/Jun/20
thank you sir mind.
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}\:\mathrm{mind}. \\ $$
Commented by maths mind last updated on 23/Jun/20
withe pleasur
$${withe}\:{pleasur} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *