Question Number 124632 by liberty last updated on 05/Dec/20
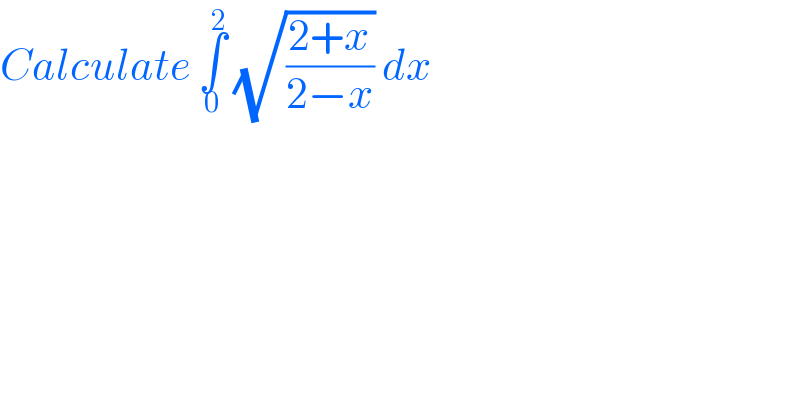
$${Calculate}\:\underset{\mathrm{0}} {\overset{\mathrm{2}} {\int}}\:\sqrt{\frac{\mathrm{2}+{x}}{\mathrm{2}−{x}}}\:{dx}\: \\ $$
Answered by bemath last updated on 05/Dec/20
![put x=2cos 2θ I=∫_(π/4) ^0 (√((2+2cos 2θ)/(2−2cos 2θ))) (−4sin 2θ) dθ I= 4∫_0 ^(π/4) (√((1+cos 2θ)/(1−cos 2θ))) (2sin θ cos θ)dθ I= 4∫_0 ^(π/4) 2cos^2 θ dθ I=4 [ ((sin 2θ)/2) + θ ]_( 0) ^(π/4) = 4((1/2)+(π/4)) I=2+π](https://www.tinkutara.com/question/Q124633.png)
$${put}\:{x}=\mathrm{2cos}\:\mathrm{2}\theta\: \\ $$$${I}=\underset{\pi/\mathrm{4}} {\overset{\mathrm{0}} {\int}}\sqrt{\frac{\mathrm{2}+\mathrm{2cos}\:\mathrm{2}\theta}{\mathrm{2}−\mathrm{2cos}\:\mathrm{2}\theta}}\:\left(−\mathrm{4sin}\:\mathrm{2}\theta\right)\:{d}\theta \\ $$$${I}=\:\mathrm{4}\underset{\mathrm{0}} {\overset{\pi/\mathrm{4}} {\int}}\:\sqrt{\frac{\mathrm{1}+\mathrm{cos}\:\mathrm{2}\theta}{\mathrm{1}−\mathrm{cos}\:\mathrm{2}\theta}}\:\left(\mathrm{2sin}\:\theta\:\mathrm{cos}\:\theta\right){d}\theta \\ $$$${I}=\:\mathrm{4}\underset{\mathrm{0}} {\overset{\pi/\mathrm{4}} {\int}}\:\mathrm{2cos}\:^{\mathrm{2}} \theta\:{d}\theta \\ $$$${I}=\mathrm{4}\:\left[\:\frac{\mathrm{sin}\:\mathrm{2}\theta}{\mathrm{2}}\:+\:\theta\:\right]_{\:\mathrm{0}} ^{\pi/\mathrm{4}} =\:\mathrm{4}\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\pi}{\mathrm{4}}\right) \\ $$$${I}=\mathrm{2}+\pi \\ $$
Answered by mathmax by abdo last updated on 05/Dec/20
![A =∫_0 ^2 (√((2+x)/(2−x)))dx we do the changement x=2cost ⇒ A =∫_(π/2) ^0 (√((1+cost)/(1−cost)))(−2sint)dt =2∫_0 ^(π/2) ((cos((t/2)))/(sin((t/2))))×2cos((t/2))sin((t/2))dt =4 ∫_0 ^(π/2) cos^2 ((t/2))dt =4∫_0 ^(π/2) ((1+cost)/2)dt =2∫_0 ^(π/2) (1+cost)dt =π+2[sint]_0 ^(π/2) =π +2](https://www.tinkutara.com/question/Q124667.png)
$$\mathrm{A}\:=\int_{\mathrm{0}} ^{\mathrm{2}} \sqrt{\frac{\mathrm{2}+\mathrm{x}}{\mathrm{2}−\mathrm{x}}}\mathrm{dx}\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\mathrm{x}=\mathrm{2cost}\:\Rightarrow \\ $$$$\mathrm{A}\:=\int_{\frac{\pi}{\mathrm{2}}} ^{\mathrm{0}} \sqrt{\frac{\mathrm{1}+\mathrm{cost}}{\mathrm{1}−\mathrm{cost}}}\left(−\mathrm{2sint}\right)\mathrm{dt}\:=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{cos}\left(\frac{\mathrm{t}}{\mathrm{2}}\right)}{\mathrm{sin}\left(\frac{\mathrm{t}}{\mathrm{2}}\right)}×\mathrm{2cos}\left(\frac{\mathrm{t}}{\mathrm{2}}\right)\mathrm{sin}\left(\frac{\mathrm{t}}{\mathrm{2}}\right)\mathrm{dt} \\ $$$$=\mathrm{4}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{cos}^{\mathrm{2}} \left(\frac{\mathrm{t}}{\mathrm{2}}\right)\mathrm{dt}\:=\mathrm{4}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}+\mathrm{cost}}{\mathrm{2}}\mathrm{dt}\:=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{1}+\mathrm{cost}\right)\mathrm{dt} \\ $$$$=\pi+\mathrm{2}\left[\mathrm{sint}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:=\pi\:+\mathrm{2} \\ $$
Answered by MJS_new last updated on 05/Dec/20
![∫_0 ^2 (√((2+x)/(2−x)))dx= [t=(√((2−x)/(2+x))) → dx=−(1/2)(x+2)^(3/2) (√(2−x))dt] =8∫_0 ^1 (dt/((t^2 +1)^2 ))=[((4t)/(t^2 +1))+4arctan t]_0 ^1 =π+2](https://www.tinkutara.com/question/Q124732.png)
$$\underset{\mathrm{0}} {\overset{\mathrm{2}} {\int}}\sqrt{\frac{\mathrm{2}+{x}}{\mathrm{2}−{x}}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\sqrt{\frac{\mathrm{2}−{x}}{\mathrm{2}+{x}}}\:\rightarrow\:{dx}=−\frac{\mathrm{1}}{\mathrm{2}}\left({x}+\mathrm{2}\right)^{\mathrm{3}/\mathrm{2}} \sqrt{\mathrm{2}−{x}}{dt}\right] \\ $$$$=\mathrm{8}\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\frac{{dt}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }=\left[\frac{\mathrm{4}{t}}{{t}^{\mathrm{2}} +\mathrm{1}}+\mathrm{4arctan}\:{t}\right]_{\mathrm{0}} ^{\mathrm{1}} =\pi+\mathrm{2} \\ $$
