Question Number 93249 by 1549442205 last updated on 12/May/20
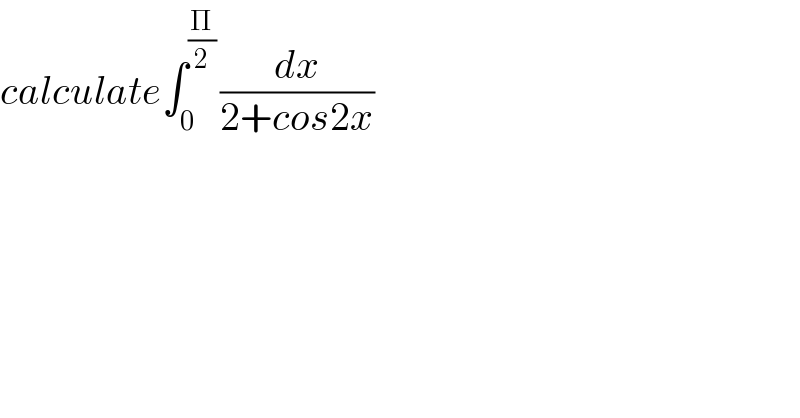
$${calculate}\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}\:} \frac{{dx}}{\mathrm{2}+{cos}\mathrm{2}{x}} \\ $$
Commented by 1549442205 last updated on 12/May/20
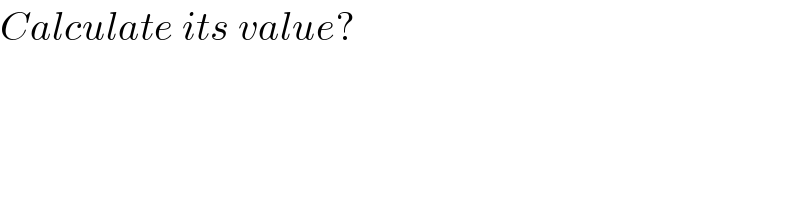
$${Calculate}\:{its}\:{value}? \\ $$
Commented by abdomathmax last updated on 12/May/20
![I = ∫_0 ^(π/2) (dx/(2+cos(2x))) ⇒I =_(2x=t) (1/2)∫_0 ^π (dt/(2+cost)) =_(tan((t/2))=u) (1/2)∫_0 ^∞ ((2du)/((1+u^2 )(2+((1−u^2 )/(1+u^2 ))))) =∫_0 ^∞ (du/(2+2u^2 +1−u^2 )) =∫_0 ^∞ (du/(3+u^2 )) =_(u=(√3)z) =∫_0 ^∞ (((√3)dz)/(3(1+z^2 ))) =(1/( (√3)))[arctanz]_0 ^(+∞) =(1/( (√3)))×(π/2) ⇒ I =(π/(2(√3)))](https://www.tinkutara.com/question/Q93263.png)
$${I}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{dx}}{\mathrm{2}+{cos}\left(\mathrm{2}{x}\right)}\:\Rightarrow{I}\:=_{\mathrm{2}{x}={t}} \:\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\pi} \:\frac{{dt}}{\mathrm{2}+{cost}} \\ $$$$=_{{tan}\left(\frac{{t}}{\mathrm{2}}\right)={u}} \:\:\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{2}{du}}{\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\left(\mathrm{2}+\frac{\mathrm{1}−{u}^{\mathrm{2}} }{\mathrm{1}+{u}^{\mathrm{2}} }\right)} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{du}}{\mathrm{2}+\mathrm{2}{u}^{\mathrm{2}} \:+\mathrm{1}−{u}^{\mathrm{2}} }\:=\int_{\mathrm{0}} ^{\infty} \:\frac{{du}}{\mathrm{3}+{u}^{\mathrm{2}} }\:=_{{u}=\sqrt{\mathrm{3}}{z}} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\sqrt{\mathrm{3}}{dz}}{\mathrm{3}\left(\mathrm{1}+{z}^{\mathrm{2}} \right)}\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\left[{arctanz}\right]_{\mathrm{0}} ^{+\infty} \:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}×\frac{\pi}{\mathrm{2}}\:\Rightarrow \\ $$$${I}\:=\frac{\pi}{\mathrm{2}\sqrt{\mathrm{3}}} \\ $$$$ \\ $$
Commented by 1549442205 last updated on 12/May/20
$${Thank}\:{you}\:{very}\:{much}! \\ $$
Commented by mathmax by abdo last updated on 12/May/20

$${you}\:{are}\:{welcome}. \\ $$
