Question Number 93265 by abdomathmax last updated on 12/May/20
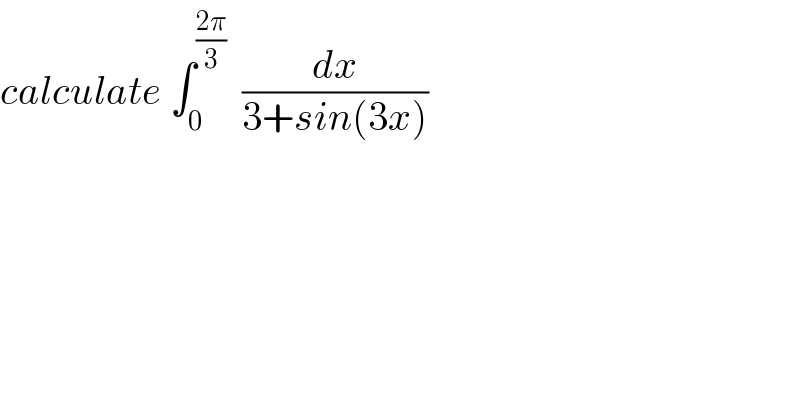
$${calculate}\:\int_{\mathrm{0}} ^{\frac{\mathrm{2}\pi}{\mathrm{3}}} \:\:\frac{{dx}}{\mathrm{3}+{sin}\left(\mathrm{3}{x}\right)} \\ $$
Commented by mathmax by abdo last updated on 12/May/20

$${A}\:=\int_{\mathrm{0}} ^{\frac{\mathrm{2}\pi}{\mathrm{3}}} \:\frac{{dx}}{\mathrm{3}+{sin}\left(\mathrm{3}{x}\right)}\:\Rightarrow\:{A}\:=_{\mathrm{3}{x}={t}} \:\:\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\:\frac{{dt}}{\mathrm{3}+{sint}} \\ $$$$=_{{e}^{{it}} \:={z}} \:\:\:\frac{\mathrm{1}}{\mathrm{3}}\:\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\:\frac{\mathrm{1}}{\mathrm{3}+\frac{{z}−{z}^{−\mathrm{1}} }{\mathrm{2}{i}}}×\frac{{dz}}{{iz}} \\ $$$$\mathrm{3}{A}\:=\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\:\frac{\mathrm{2}{idz}}{{iz}\left(\mathrm{6}{i}\:+{z}−{z}^{−\mathrm{1}} \right)}\:=\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\:\frac{\mathrm{2}{dz}}{\mathrm{6}{iz}\:+{z}^{\mathrm{2}} −\mathrm{1}} \\ $$$${let}\:\varphi\left({z}\right)\:=\frac{\mathrm{2}}{{z}^{\mathrm{2}} \:+\mathrm{6}{iz}\:−\mathrm{1}}\:\:{poles}\:{of}\:\varphi? \\ $$$${z}^{\mathrm{2}} \:+\mathrm{6}{iz}\:−\mathrm{1}\:=\mathrm{0}\rightarrow\:\Delta^{'} \:=\left(\mathrm{3}{i}\right)^{\mathrm{2}} +\mathrm{1}\:=−\mathrm{8}\:\Rightarrow{z}_{\mathrm{1}} =−\mathrm{3}{i}+\mathrm{2}{i}\sqrt{\mathrm{2}} \\ $$$${z}_{\mathrm{2}} =−\mathrm{3}{i}−\mathrm{2}{i}\sqrt{\mathrm{2}}\:\:\:\:{we}\:{have}\:\mid{z}_{\mathrm{1}} \mid−\mathrm{1}\:=\mid\mathrm{3}−\sqrt{\mathrm{2}}\mid−\mathrm{1}\:=\mathrm{3}−\sqrt{\mathrm{2}}−\mathrm{1}\:=\mathrm{2}−\sqrt{\mathrm{2}}>\mathrm{0} \\ $$$$\mid{z}_{\mathrm{2}} \mid\:−\mathrm{1}\:=\mathrm{3}+\sqrt{\mathrm{2}}−\mathrm{1}\:=\mathrm{2}+\sqrt{\mathrm{2}}>\mathrm{0}\:\Rightarrow{Res}\left(\varphi,{z}_{\mathrm{1}} \right)={Res}\left(\varphi,{z}_{\mathrm{2}} \right)=\mathrm{0}\:\Rightarrow \\ $$$$\Sigma\:{Res}\:=\mathrm{0}\:\Rightarrow{A}\:=\mathrm{0} \\ $$
Answered by niroj last updated on 12/May/20
![∫_0 ^( ((2π)/3)) (( dx)/(3 + sin (3x))) Put , 3x= t 3dx=dt dx=(1/3)dt IF x=((2π)/3) ⇒ t= 2π IF x=0 ⇒ t=0 (1/3)∫_0 ^( 2π) (( 1)/(3+sin t))dt =[ (1/3)∫ (( 1)/(3+ ((2tan(t/2))/(1+tan^2 (t/2)))))dt]_0 2π = [ (1/3)∫(( sec^2 (t/2))/(3+3tan^2 (t/2)+2tan(t/2)))dt]_0 ^(2π) Put, tan (t/2)= m sec^2 (t/2)dt=2dm [ (1/3)∫ ((2dm)/(3+3m^2 +2m))]_0 ^(2π) = [(2/3)∫ (1/(3(m^2 +(2/3)m+1)))dm]_0 ^(2π) = [ (2/9)∫ (( 1)/((m)^2 +2.(1/3).m+(1/9)−(1/9)+1))dm]_0 ^(2π) = [ (2/9)∫ (( 1)/((m+(1/3))^2 −((8/9))))dm]_0 ^(2π) = [ (2/9)∫ (1/((m+(1/3))^2 −(((√8)/3))^2 ))dm]_0 ^(2π) = [(2/9).(1/(2.((√8)/3)))log (( m+(1/3) +((√8)/3))/(m+(1/3) −((√8)/3)))]_0 ^(2π) =[ (1/(3(√8))) log ((3m+1+(√8))/(3m+1−(√8)))]_0 ^(2π) = [(1/(3(√8)))log ((3 tan(t/2) +1+(√8))/(3tan(t/2) +1−(√8)))]_0 ^(2π) = {(1/(3(√8)))log ((3tan ((2π)/2)+1+(√8))/(3tan((2π)/2)+1−(√8)))}−{(1/(3(√8)))log ((3.0+1+(√8))/(3.0+1−(√8)))} = (1/(3(√8))) log ((1+(√8))/(1−(√8))) −(1/(3(√8)))log ((1+(√8))/(1−(√8))) = 0 //.](https://www.tinkutara.com/question/Q93273.png)
$$\:\:\int_{\mathrm{0}} ^{\:\frac{\mathrm{2}\pi}{\mathrm{3}}} \:\:\:\frac{\:\mathrm{dx}}{\mathrm{3}\:+\:\mathrm{sin}\:\left(\mathrm{3x}\right)} \\ $$$$\:\:\mathrm{Put}\:,\:\mathrm{3x}=\:\mathrm{t} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{3dx}=\mathrm{dt} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{dx}=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{dt} \\ $$$$\:\mathrm{IF}\:\mathrm{x}=\frac{\mathrm{2}\pi}{\mathrm{3}}\:\Rightarrow\:\:\mathrm{t}=\:\mathrm{2}\pi \\ $$$$\:\mathrm{IF}\:\mathrm{x}=\mathrm{0}\:\Rightarrow\:\:\mathrm{t}=\mathrm{0} \\ $$$$\:\:\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\:\mathrm{2}\pi} \:\:\frac{\:\mathrm{1}}{\mathrm{3}+\mathrm{sin}\:\mathrm{t}}\mathrm{dt} \\ $$$$\:\:\:=\left[\:\frac{\mathrm{1}}{\mathrm{3}}\int\:\frac{\:\:\mathrm{1}}{\mathrm{3}+\:\frac{\mathrm{2tan}\frac{\mathrm{t}}{\mathrm{2}}}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \frac{\mathrm{t}}{\mathrm{2}}}}\mathrm{dt}\right]_{\mathrm{0}} \mathrm{2}\pi \\ $$$$\:=\:\:\left[\:\:\frac{\mathrm{1}}{\mathrm{3}}\int\frac{\:\mathrm{sec}^{\mathrm{2}} \frac{\mathrm{t}}{\mathrm{2}}}{\mathrm{3}+\mathrm{3tan}^{\mathrm{2}} \frac{\mathrm{t}}{\mathrm{2}}+\mathrm{2tan}\frac{\mathrm{t}}{\mathrm{2}}}\mathrm{dt}\right]_{\mathrm{0}} ^{\mathrm{2}\pi} \\ $$$$\:\:\:\mathrm{Put},\:\mathrm{tan}\:\frac{\mathrm{t}}{\mathrm{2}}=\:\mathrm{m} \\ $$$$\:\:\:\:\:\:\mathrm{sec}^{\mathrm{2}} \frac{\mathrm{t}}{\mathrm{2}}\mathrm{dt}=\mathrm{2dm} \\ $$$$\:\left[\:\frac{\mathrm{1}}{\mathrm{3}}\int\:\frac{\mathrm{2dm}}{\mathrm{3}+\mathrm{3m}^{\mathrm{2}} +\mathrm{2m}}\right]_{\mathrm{0}} ^{\mathrm{2}\pi} \\ $$$$\:=\:\left[\frac{\mathrm{2}}{\mathrm{3}}\int\:\:\frac{\mathrm{1}}{\mathrm{3}\left(\mathrm{m}^{\mathrm{2}} +\frac{\mathrm{2}}{\mathrm{3}}\mathrm{m}+\mathrm{1}\right)}\mathrm{dm}\right]_{\mathrm{0}} ^{\mathrm{2}\pi} \\ $$$$=\:\left[\:\frac{\mathrm{2}}{\mathrm{9}}\int\:\frac{\:\:\:\mathrm{1}}{\left(\mathrm{m}\right)^{\mathrm{2}} +\mathrm{2}.\frac{\mathrm{1}}{\mathrm{3}}.\mathrm{m}+\frac{\mathrm{1}}{\mathrm{9}}−\frac{\mathrm{1}}{\mathrm{9}}+\mathrm{1}}\mathrm{dm}\right]_{\mathrm{0}} ^{\mathrm{2}\pi} \\ $$$$=\:\left[\:\frac{\mathrm{2}}{\mathrm{9}}\int\:\frac{\:\:\mathrm{1}}{\left(\mathrm{m}+\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} −\left(\frac{\mathrm{8}}{\mathrm{9}}\right)}\mathrm{dm}\right]_{\mathrm{0}} ^{\mathrm{2}\pi} \\ $$$$\:=\:\left[\:\frac{\mathrm{2}}{\mathrm{9}}\int\:\frac{\mathrm{1}}{\left(\mathrm{m}+\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} −\left(\frac{\sqrt{\mathrm{8}}}{\mathrm{3}}\right)^{\mathrm{2}} }\mathrm{dm}\right]_{\mathrm{0}} ^{\mathrm{2}\pi} \\ $$$$\:=\:\left[\frac{\mathrm{2}}{\mathrm{9}}.\frac{\mathrm{1}}{\mathrm{2}.\frac{\sqrt{\mathrm{8}}}{\mathrm{3}}}\mathrm{log}\:\frac{\:\mathrm{m}+\frac{\mathrm{1}}{\mathrm{3}}\:+\frac{\sqrt{\mathrm{8}}}{\mathrm{3}}}{\mathrm{m}+\frac{\mathrm{1}}{\mathrm{3}}\:−\frac{\sqrt{\mathrm{8}}}{\mathrm{3}}}\right]_{\mathrm{0}} ^{\mathrm{2}\pi} \\ $$$$\:=\left[\:\frac{\mathrm{1}}{\mathrm{3}\sqrt{\mathrm{8}}}\:\mathrm{log}\:\frac{\mathrm{3m}+\mathrm{1}+\sqrt{\mathrm{8}}}{\mathrm{3m}+\mathrm{1}−\sqrt{\mathrm{8}}}\right]_{\mathrm{0}} ^{\mathrm{2}\pi} \\ $$$$\:=\:\left[\frac{\mathrm{1}}{\mathrm{3}\sqrt{\mathrm{8}}}\mathrm{log}\:\frac{\mathrm{3}\:\mathrm{tan}\frac{\mathrm{t}}{\mathrm{2}}\:+\mathrm{1}+\sqrt{\mathrm{8}}}{\mathrm{3tan}\frac{\mathrm{t}}{\mathrm{2}}\:+\mathrm{1}−\sqrt{\mathrm{8}}}\right]_{\mathrm{0}} ^{\mathrm{2}\pi} \\ $$$$\:=\:\left\{\frac{\mathrm{1}}{\mathrm{3}\sqrt{\mathrm{8}}}\mathrm{log}\:\frac{\mathrm{3tan}\:\frac{\mathrm{2}\pi}{\mathrm{2}}+\mathrm{1}+\sqrt{\mathrm{8}}}{\mathrm{3tan}\frac{\mathrm{2}\pi}{\mathrm{2}}+\mathrm{1}−\sqrt{\mathrm{8}}}\right\}−\left\{\frac{\mathrm{1}}{\mathrm{3}\sqrt{\mathrm{8}}}\mathrm{log}\:\frac{\mathrm{3}.\mathrm{0}+\mathrm{1}+\sqrt{\mathrm{8}}}{\mathrm{3}.\mathrm{0}+\mathrm{1}−\sqrt{\mathrm{8}}}\right\} \\ $$$$\:=\:\frac{\mathrm{1}}{\mathrm{3}\sqrt{\mathrm{8}}}\:\mathrm{log}\:\frac{\mathrm{1}+\sqrt{\mathrm{8}}}{\mathrm{1}−\sqrt{\mathrm{8}}}\:−\frac{\mathrm{1}}{\mathrm{3}\sqrt{\mathrm{8}}}\mathrm{log}\:\frac{\mathrm{1}+\sqrt{\mathrm{8}}}{\mathrm{1}−\sqrt{\mathrm{8}}} \\ $$$$=\:\mathrm{0}\://. \\ $$
