Question Number 62732 by mathmax by abdo last updated on 24/Jun/19
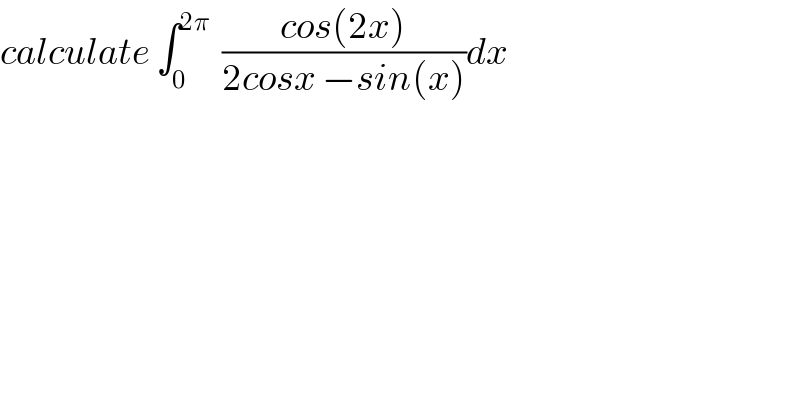
$${calculate}\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\frac{{cos}\left(\mathrm{2}{x}\right)}{\mathrm{2}{cosx}\:−{sin}\left({x}\right)}{dx}\: \\ $$
Answered by MJS last updated on 24/Jun/19
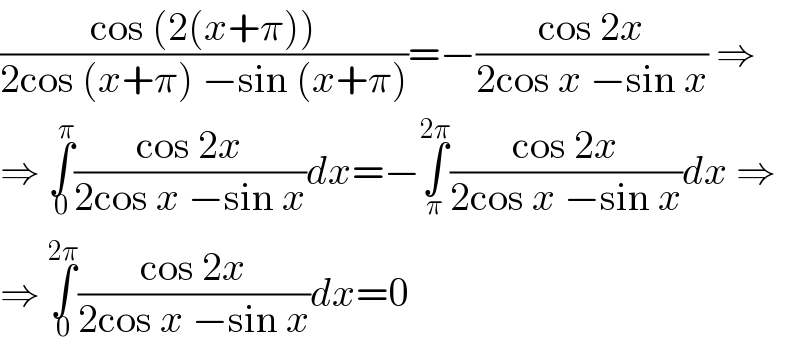
$$\frac{\mathrm{cos}\:\left(\mathrm{2}\left({x}+\pi\right)\right)}{\mathrm{2cos}\:\left({x}+\pi\right)\:−\mathrm{sin}\:\left({x}+\pi\right)}=−\frac{\mathrm{cos}\:\mathrm{2}{x}}{\mathrm{2cos}\:{x}\:−\mathrm{sin}\:{x}}\:\Rightarrow \\ $$$$\Rightarrow\:\underset{\mathrm{0}} {\overset{\pi} {\int}}\frac{\mathrm{cos}\:\mathrm{2}{x}}{\mathrm{2cos}\:{x}\:−\mathrm{sin}\:{x}}{dx}=−\underset{\pi} {\overset{\mathrm{2}\pi} {\int}}\frac{\mathrm{cos}\:\mathrm{2}{x}}{\mathrm{2cos}\:{x}\:−\mathrm{sin}\:{x}}{dx}\:\Rightarrow \\ $$$$\Rightarrow\:\underset{\mathrm{0}} {\overset{\mathrm{2}\pi} {\int}}\frac{\mathrm{cos}\:\mathrm{2}{x}}{\mathrm{2cos}\:{x}\:−\mathrm{sin}\:{x}}{dx}=\mathrm{0} \\ $$
Commented by mathmax by abdo last updated on 24/Jun/19

$${thank}\:{you}\:{sir}\:. \\ $$
