Menu Close

calculate-0-2pi-ln-x-2-2xcos-1-d-

Tinku Tara 0 Comments
Pin




Question Number 130536 by mathmax by abdo last updated on 26/Jan/21
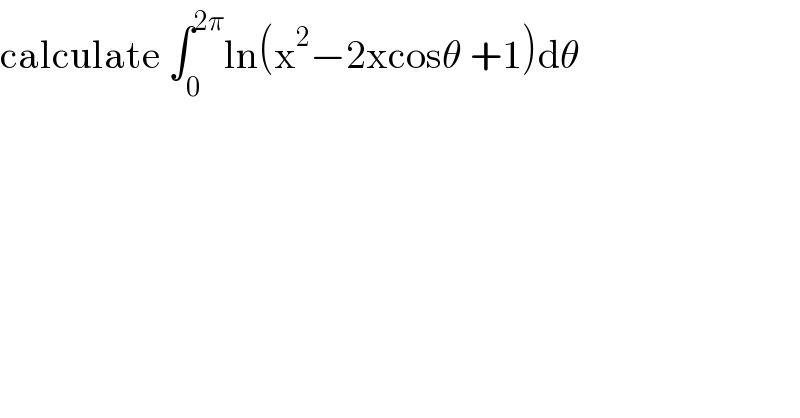
calculate ∫_0 ^(2π) ln(x^2 −2xcosθ +1)dθ
$$\mathrm{calculate}\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \mathrm{ln}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{2xcos}\theta\:+\mathrm{1}\right)\mathrm{d}\theta \\ $$
Answered by Ar Brandon last updated on 26/Jan/21
1. 1−2acos(x)+a^2 =cos^2 −2acos(x)+a^2 +sin^2 (x) =(cos(x)−a)^2 +sin^2 (x)>0 2. 1−2a cos((2kπ)/n)+a^2 =(cos((2kπ)/n)−a)^2 +sin^2 ((2kπ)/n) =(cos((2kπ)/n)−a)^2 −(isin((2kπ)/n))^2 =(cos((2kπ)/n)−isin((2kπ)/n)−a)(cos((2kπ)/n)+isin((2kπ)/n)−a) =(a−e^(2ikπ/n) )(a−e^(−2ikπ/n) ) 3. See Mr 1549442205PVT ′s explanation on Q107498 4. I=∫_0 ^(2π) ln(1−2a cos(x)+a^2 )dx =lim_(n→∞) ((2π)/n)Σ_(k=1) ^n ln(1−2a cos(((2πk)/n))+a^2 ) =lim_(n→∞) ((2π)/n)lnΠ_(k=1) ^n (1−2a cos(((2πk)/n))+a^2 ) =lim_(n→∞) ((2π)/n)ln(a^n −1)^2 =lim_(n→∞) ((4π)/n)ln(a^n −1) =4πlim_(n→∞) [((ln(a^n −1))/n)]=4πlim_(n→∞) [((a^n lna)/(a^n −1))] =4πln(a)
$$\mathrm{1}.\:\:\mathrm{1}−\mathrm{2acos}\left(\mathrm{x}\right)+\mathrm{a}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{cos}^{\mathrm{2}} −\mathrm{2acos}\left(\mathrm{x}\right)+\mathrm{a}^{\mathrm{2}} +\mathrm{sin}^{\mathrm{2}} \left(\mathrm{x}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(\mathrm{cos}\left(\mathrm{x}\right)−\mathrm{a}\right)^{\mathrm{2}} +\mathrm{sin}^{\mathrm{2}} \left(\mathrm{x}\right)>\mathrm{0} \\ $$$$\mathrm{2}.\:\:\mathrm{1}−\mathrm{2a}\:\mathrm{cos}\frac{\mathrm{2k}\pi}{\mathrm{n}}+\mathrm{a}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(\mathrm{cos}\frac{\mathrm{2k}\pi}{\mathrm{n}}−\mathrm{a}\right)^{\mathrm{2}} +\mathrm{sin}^{\mathrm{2}} \frac{\mathrm{2k}\pi}{\mathrm{n}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(\mathrm{cos}\frac{\mathrm{2k}\pi}{\mathrm{n}}−\mathrm{a}\right)^{\mathrm{2}} −\left(\mathrm{isin}\frac{\mathrm{2k}\pi}{\mathrm{n}}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(\mathrm{cos}\frac{\mathrm{2k}\pi}{\mathrm{n}}−\mathrm{isin}\frac{\mathrm{2k}\pi}{\mathrm{n}}−\mathrm{a}\right)\left(\mathrm{cos}\frac{\mathrm{2k}\pi}{\mathrm{n}}+\mathrm{isin}\frac{\mathrm{2k}\pi}{\mathrm{n}}−\mathrm{a}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(\mathrm{a}−\mathrm{e}^{\mathrm{2ik}\pi/\mathrm{n}} \right)\left(\mathrm{a}−\mathrm{e}^{−\mathrm{2ik}\pi/\mathrm{n}} \right) \\ $$$$\mathrm{3}.\:{See}\:{Mr}\:\mathrm{1549442205}{PVT}\:'\mathrm{s}\:{explanation}\:{on}\:{Q}\mathrm{107498} \\ $$$$\mathrm{4}.\:\:\mathrm{I}=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \mathrm{ln}\left(\mathrm{1}−\mathrm{2a}\:\mathrm{cos}\left(\mathrm{x}\right)+\mathrm{a}^{\mathrm{2}} \right)\mathrm{dx} \\ $$$$\:\:\:\:\:\:\:\:=\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{2}\pi}{\mathrm{n}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\mathrm{ln}\left(\mathrm{1}−\mathrm{2a}\:\mathrm{cos}\left(\frac{\mathrm{2}\pi\mathrm{k}}{\mathrm{n}}\right)+\mathrm{a}^{\mathrm{2}} \right) \\ $$$$\:\:\:\:\:\:\:\:=\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{2}\pi}{\mathrm{n}}\mathrm{ln}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\prod}}\left(\mathrm{1}−\mathrm{2a}\:\mathrm{cos}\left(\frac{\mathrm{2}\pi\mathrm{k}}{\mathrm{n}}\right)+\mathrm{a}^{\mathrm{2}} \right) \\ $$$$\:\:\:\:\:\:\:\:=\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{2}\pi}{\mathrm{n}}\mathrm{ln}\left(\mathrm{a}^{\mathrm{n}} −\mathrm{1}\right)^{\mathrm{2}} =\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{4}\pi}{\mathrm{n}}\mathrm{ln}\left(\mathrm{a}^{\mathrm{n}} −\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:=\mathrm{4}\pi\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\left[\frac{\mathrm{ln}\left(\mathrm{a}^{\mathrm{n}} −\mathrm{1}\right)}{\mathrm{n}}\right]=\mathrm{4}\pi\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\left[\frac{\mathrm{a}^{\mathrm{n}} \mathrm{lna}}{\mathrm{a}^{\mathrm{n}} −\mathrm{1}}\right] \\ $$$$\:\:\:\:\:\:\:\:=\mathrm{4}\pi\mathrm{ln}\left(\mathrm{a}\right) \\ $$
Answered by mathmax by abdo last updated on 26/Jan/21
let f(x)=∫_0 ^(2π) ln(x^2 −2xcosθ+1)dθ ⇒f^′ (x)=∫_0 ^(2π) ((2x−2cosθ)/(x^2 −2xcosθ +1))dθ =_(e^(iθ) =z) ∫_(∣z∣=1) ((2x−2((z+z^(−1) )/2))/(x^2 −2x((z+z^(−1) )/2)+1))(dz/(iz)) =∫_(∣z∣=1) ((2x−z−z^(−1) )/(x^2 +1−xz−xz^(−1) )iz))dz =(1/i)∫_(∣z∣=1) ((2x−z−z^(−1) )/((x^2 +1)z−xz^2 −x))dz =(1/i)∫_(∣z∣=1) ((2xz−z^2 −1)/(−xz^2 +(x^2 +1)z−x))dz =−i∫_(∣z∣=1) ((z^2 −2xz+1)/(z(xz^2 −(x^2 +1)z+x)))dz ϕ(z)=((z^2 −2xz+1)/(z(xz^2 −(x^2 +1)z+x))) poles of ϕ! Δ=(x^2 +1)^2 −4x^2 =x^4 +2x^2 +1−4x^2 =(x^2 −1)^2 ⇒z_1 =((x^2 +1+∣x^2 −1∣)/(2x)) and z_2 =((x^2 +1−∣x^2 −1∣)/(2x)) case1 ∣x∣>1 ⇒z_1 =((2x^2 )/(2x))=x and z_2 =(2/(2x))=(1/x) ⇒∣z_2 ∣=(1/(∣x∣))<1 ⇒ ∫_R ϕ(z)dz =2iπ{Res(ϕ,z_2 )} ϕ(z)=((z^2 −2xz+1)/(zx(z−z_1 )(z−z_2 ))) ⇒Res(ϕ,o) =(1/(z_1 z_2 ))=1 Res(ϕ,z_2 )=((z_2 ^2 −2xz_2 +1)/(z_2 x((1/x)−x)))=(((1/x^2 )−2+1)/(1−x^2 ))×x=((1−x^2 )/(x^2 (1−x^2 ))).x=(1/x) ∫_R ϕ(z)dz =2iπ{(1/x)} =((2iπ)/x) ⇒f^′ (x)=−i(((2iπ)/x))=((2π)/x) ⇒ f(x)=2πln∣x∣ +c_0 c_0 =f(1) =∫_0 ^(2π) ln(2−2cosθ)dθ =2πln(2)+∫_0 ^(2π) ln(2sin^2 ((θ/2)))dθ =4πln(2)+2∫_0 ^(2π) ln(sin((θ/2)))dθ((θ/2)=t) =4πln(2)+4∫_0 ^π ln(sin(t))dt but ∫_0 ^π ln(sint)dt =∫_0 ^(π/2) ln(sint)dt +∫_(π/2) ^π ln(sint)dt = =−(π/2)ln2−(π/2)ln2 =−πln2 ⇒c_0 =4πln2−4πln2 =0 ⇒ f(x)=2πln∣x∣ case 2 ∣x∣<1 we get z_1 =(1/x) and z_2 =x due to symetrie we get the same value ⇒f(x)=2πln∣x∣
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \mathrm{ln}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{2xcos}\theta+\mathrm{1}\right)\mathrm{d}\theta\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{x}\right)=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\frac{\mathrm{2x}−\mathrm{2cos}\theta}{\mathrm{x}^{\mathrm{2}} −\mathrm{2xcos}\theta\:+\mathrm{1}}\mathrm{d}\theta \\ $$$$=_{\mathrm{e}^{\mathrm{i}\theta} \:=\mathrm{z}} \:\:\:\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\:\frac{\mathrm{2x}−\mathrm{2}\frac{\mathrm{z}+\mathrm{z}^{−\mathrm{1}} }{\mathrm{2}}}{\mathrm{x}^{\mathrm{2}} −\mathrm{2x}\frac{\mathrm{z}+\mathrm{z}^{−\mathrm{1}} }{\mathrm{2}}+\mathrm{1}}\frac{\mathrm{dz}}{\mathrm{iz}} \\ $$$$=\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\:\frac{\mathrm{2x}−\mathrm{z}−\mathrm{z}^{−\mathrm{1}} }{\left.\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}−\mathrm{xz}−\mathrm{xz}^{−\mathrm{1}} \right)\mathrm{iz}}\mathrm{dz}\:=\frac{\mathrm{1}}{\mathrm{i}}\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\frac{\mathrm{2x}−\mathrm{z}−\mathrm{z}^{−\mathrm{1}} }{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)\mathrm{z}−\mathrm{xz}^{\mathrm{2}} −\mathrm{x}}\mathrm{dz} \\ $$$$=\frac{\mathrm{1}}{\mathrm{i}}\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\:\frac{\mathrm{2xz}−\mathrm{z}^{\mathrm{2}} −\mathrm{1}}{−\mathrm{xz}^{\mathrm{2}} +\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)\mathrm{z}−\mathrm{x}}\mathrm{dz}\:=−\mathrm{i}\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\frac{\mathrm{z}^{\mathrm{2}} −\mathrm{2xz}+\mathrm{1}}{\mathrm{z}\left(\mathrm{xz}^{\mathrm{2}} −\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)\mathrm{z}+\mathrm{x}\right)}\mathrm{dz} \\ $$$$\varphi\left(\mathrm{z}\right)=\frac{\mathrm{z}^{\mathrm{2}} −\mathrm{2xz}+\mathrm{1}}{\mathrm{z}\left(\mathrm{xz}^{\mathrm{2}} −\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)\mathrm{z}+\mathrm{x}\right)}\:\mathrm{poles}\:\mathrm{of}\:\varphi! \\ $$$$\Delta=\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{4x}^{\mathrm{2}} \:=\mathrm{x}^{\mathrm{4}} +\mathrm{2x}^{\mathrm{2}} +\mathrm{1}−\mathrm{4x}^{\mathrm{2}} \:=\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{z}_{\mathrm{1}} =\frac{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}+\mid\mathrm{x}^{\mathrm{2}} −\mathrm{1}\mid}{\mathrm{2x}}\:\mathrm{and}\:\mathrm{z}_{\mathrm{2}} =\frac{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}−\mid\mathrm{x}^{\mathrm{2}} −\mathrm{1}\mid}{\mathrm{2x}} \\ $$$$\mathrm{case1}\:\:\:\mid\mathrm{x}\mid>\mathrm{1}\:\Rightarrow\mathrm{z}_{\mathrm{1}} =\frac{\mathrm{2x}^{\mathrm{2}} }{\mathrm{2x}}=\mathrm{x}\:\mathrm{and}\:\mathrm{z}_{\mathrm{2}} =\frac{\mathrm{2}}{\mathrm{2x}}=\frac{\mathrm{1}}{\mathrm{x}}\:\Rightarrow\mid\mathrm{z}_{\mathrm{2}} \mid=\frac{\mathrm{1}}{\mid\mathrm{x}\mid}<\mathrm{1}\:\Rightarrow \\ $$$$\int_{\mathrm{R}} \varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\left\{\mathrm{Res}\left(\varphi,\mathrm{z}_{\mathrm{2}} \right)\right\} \\ $$$$\varphi\left(\mathrm{z}\right)=\frac{\mathrm{z}^{\mathrm{2}} −\mathrm{2xz}+\mathrm{1}}{\mathrm{zx}\left(\mathrm{z}−\mathrm{z}_{\mathrm{1}} \right)\left(\mathrm{z}−\mathrm{z}_{\mathrm{2}} \right)}\:\Rightarrow\mathrm{Res}\left(\varphi,\mathrm{o}\right)\:=\frac{\mathrm{1}}{\mathrm{z}_{\mathrm{1}} \mathrm{z}_{\mathrm{2}} }=\mathrm{1} \\ $$$$\mathrm{Res}\left(\varphi,\mathrm{z}_{\mathrm{2}} \right)=\frac{\mathrm{z}_{\mathrm{2}} ^{\mathrm{2}} −\mathrm{2xz}_{\mathrm{2}} +\mathrm{1}}{\mathrm{z}_{\mathrm{2}} \mathrm{x}\left(\frac{\mathrm{1}}{\mathrm{x}}−\mathrm{x}\right)}=\frac{\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }−\mathrm{2}+\mathrm{1}}{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }×\mathrm{x}=\frac{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)}.\mathrm{x}=\frac{\mathrm{1}}{\mathrm{x}} \\ $$$$\int_{\mathrm{R}} \varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\left\{\frac{\mathrm{1}}{\mathrm{x}}\right\}\:=\frac{\mathrm{2i}\pi}{\mathrm{x}}\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{x}\right)=−\mathrm{i}\left(\frac{\mathrm{2i}\pi}{\mathrm{x}}\right)=\frac{\mathrm{2}\pi}{\mathrm{x}}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{2}\pi\mathrm{ln}\mid\mathrm{x}\mid\:+\mathrm{c}_{\mathrm{0}} \:\:\:\mathrm{c}_{\mathrm{0}} =\mathrm{f}\left(\mathrm{1}\right)\:=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \mathrm{ln}\left(\mathrm{2}−\mathrm{2cos}\theta\right)\mathrm{d}\theta \\ $$$$=\mathrm{2}\pi\mathrm{ln}\left(\mathrm{2}\right)+\int_{\mathrm{0}} ^{\mathrm{2}\pi} \mathrm{ln}\left(\mathrm{2sin}^{\mathrm{2}} \left(\frac{\theta}{\mathrm{2}}\right)\right)\mathrm{d}\theta\:=\mathrm{4}\pi\mathrm{ln}\left(\mathrm{2}\right)+\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{2}\pi} \mathrm{ln}\left(\mathrm{sin}\left(\frac{\theta}{\mathrm{2}}\right)\right)\mathrm{d}\theta\left(\frac{\theta}{\mathrm{2}}=\mathrm{t}\right) \\ $$$$=\mathrm{4}\pi\mathrm{ln}\left(\mathrm{2}\right)+\mathrm{4}\int_{\mathrm{0}} ^{\pi} \mathrm{ln}\left(\mathrm{sin}\left(\mathrm{t}\right)\right)\mathrm{dt}\:\mathrm{but} \\ $$$$\int_{\mathrm{0}} ^{\pi} \mathrm{ln}\left(\mathrm{sint}\right)\mathrm{dt}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{sint}\right)\mathrm{dt}\:+\int_{\frac{\pi}{\mathrm{2}}} ^{\pi} \mathrm{ln}\left(\mathrm{sint}\right)\mathrm{dt}\:= \\ $$$$=−\frac{\pi}{\mathrm{2}}\mathrm{ln2}−\frac{\pi}{\mathrm{2}}\mathrm{ln2}\:=−\pi\mathrm{ln2}\:\Rightarrow\mathrm{c}_{\mathrm{0}} =\mathrm{4}\pi\mathrm{ln2}−\mathrm{4}\pi\mathrm{ln2}\:=\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{2}\pi\mathrm{ln}\mid\mathrm{x}\mid \\ $$$$\mathrm{case}\:\mathrm{2}\:\mid\mathrm{x}\mid<\mathrm{1}\:\mathrm{we}\:\mathrm{get}\:\mathrm{z}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{x}}\:\mathrm{and}\:\mathrm{z}_{\mathrm{2}} =\mathrm{x}\:\:\mathrm{due}\:\mathrm{to}\:\mathrm{symetrie}\:\mathrm{we}\:\mathrm{get}\:\mathrm{the} \\ $$$$\mathrm{same}\:\mathrm{value}\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\mathrm{2}\pi\mathrm{ln}\mid\mathrm{x}\mid \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *