Question Number 105231 by mathmax by abdo last updated on 27/Jul/20
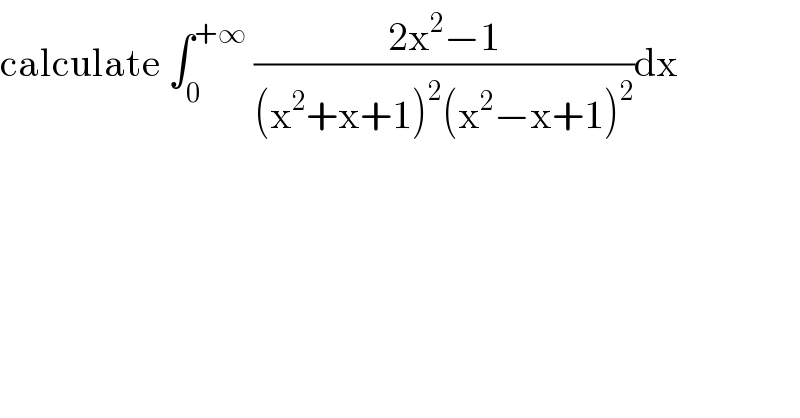
$$\mathrm{calculate}\:\int_{\mathrm{0}} ^{+\infty} \:\frac{\mathrm{2x}^{\mathrm{2}} −\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$
Answered by 1549442205PVT last updated on 27/Jul/20
![F=(1/2)∫((4x^2 )/((x^2 +x+1)^2 (x^2 −x+1)^2 ))dx−∫(dx/((x^2 +x+1)^2 (x^2 −x+1)^2 ))=∫(A)+∫(B) we have B= (1/((x^2 +x+1)^2 (x^2 −x+1)^2 ))=[(1/2)(((x+1)/((x^2 +x+1)))−((x−1)/((x^2 −x+1))))]^2 =((x^2 +2x+1)/(4(x^2 +x+1)^2 ))+((x^2 −2x+1)/(4(x^2 −x+1)^2 ))−((2x^2 −2)/(4(x^2 +x+1)(x^2 −x+1))) =(1/(4(x^2 +x+1)))+(x/(4(x^2 +x+1)^2 ))+(1/(4(x^2 −x+1)))+((−x)/(4(x^2 −x+1)^2 ))+((2x+1)/(4(x^2 +x+1)))−((2x−1)/(4(x^2 −x+1))) ((2x+2)/(4(x^2 +x+1)))−((2x−2)/(4(x^2 −x+1)))+(x/(4(x^2 +x+1)^2 ))+((−x)/(4(x^2 −x+1)^2 ))(set { ((x^2 +x+1=u)),((x^2 −x+1=v)) :} ) 4B=(x/u^2 )−(x/v^2 )+((2x+2)/u)−((2x−2)/v) A=(1/2)((1/(x^2 −x+1))−(1/(x^2 +x+1)))^2 =((1/((x^2 −x+1)^2 ))+(1/((x^2 +x+1)^2 ))−(2/((x^2 +x+1)(x^2 −x+1))))dx 2A=(1/((x^2 −x+1)^2 ))+(1/((x^2 +x+1)^2 ))+(((x−1)/(x^2 −x+1))−((x+1)/(x^2 +x+1))) =(1/u^2 )+(1/v^2 )+((x−1)/v)−((x+1)/u) ⇒4A=(2/u^2 )+(2/v^2 )+((2x−2)/v)−((2x+2)/u).Hence, 4F=4A−4B=−((x−2)/u^2 )+((x+2)/v^2 )−((4x+1))/u)+((4(x−1))/v) 4F=∫(−((x−2)/((x^2 +x+1)^2 ))+((x+2)/((x^2 −x+1)^2 ))−((4x+1))/(x^2 +x+1))+((4(x−1))/(x^2 −x+1)))dx We have:∫(dx/(x^2 +x+1))=∫((d(x+(1/2)))/((x+(1/2))^2 +(((√3)/2))^2 ))=(2/( (√3)))tan^(−1) (((x+(1/2))/((√3)/2))) =(2/( (√3)))tan^(−1) (((2x+1)/( (√3))))(as ∫(dx/((x^2 +a^2 )))=(1/a)tan^(−1) ((x/a))) Consequently, M=∫((x−2)/((x^2 +x+1)^2 ))dx=(1/2)∫((2x+1)/((x^2 +x+1)^2 ))−(5/2)∫(dx/((x^2 +x+1)^2 )) =(1/2)∫((d(x^2 +x+1))/((x^2 +x+1)^2 ))−(3/2)I_2 =−(1/(2(x^2 +x+1)^2 ))+(1/2)I_2 N=∫((x+2)/((x^2 −x+1)^2 ))dx=(1/2)∫((2x−1)/((x^2 −x+1)^2 ))dx +(5/2)∫(dx/((x^2 −x+1)^2 ))=−(1/(2(x^2 −x+1)^2 ))+(5/2).J_2 P=∫((x+1)/(x^2 +x+1))dx=(1/2)∫((2x+1)/(x^2 +x+1))dx+(1/2)∫(dx/(x^2 +x+1)) =(1/2)ln(x^2 +x+1)+(1/( (√3)))tan^(−1) (((2x+1)/( (√3)))) Q=∫((x−1)/(x^2 −x+1))dx=(1/2)ln(x^2 −x+1)−(1/( (√3)))tan^(−1) (((2x−1)/( (√3)))) We have:I_2 =∫(dt/((t^2 +a^2 )^2 ))(with t=x+(1/2) Apply current formular :I_n =(1/(2a^2 (n−1))).(t/((t^2 +a^2 )^(n−1) ))+(1/a^2 ).((2n−3)/(2n−2)).I_(n−1) we get I_2 =(2/3).((x+(1/2))/(x^2 +x+1))+(4/3).(1/2)∫((d(x+(1/2)))/((x+(1/2))^2 +(((√3)/2))^2 )) =((2x+1)/(3(x^2 +x+1)))+.(4/(3(√3)))tan^(−1) (((2x+1)/( (√3)))).Similarly, J_2 =((2x−1)/(3(x^2 −x+1)))+(4/(3(√3)))tan^(−1) (((2x−1)/( (√3)))) Finally,4F=−M+N−4P+4Q=(1/(2(x^2 +x+1)))−(1/(2(x^2 −x+1))) +(5/2){((2x+1)/(3(x^2 +x+1)))+.(4/(3(√3)))tan^(−1) (((2x+1)/( (√3)))) +[((2x−1)/(3(x^2 −x+1)))+(4/(3(√3)))tan^(−1) (((2x−1)/( (√3))))] } −2ln(x^2 +x+1)+2ln(x^2 −x+1)−(4/( (√3)))tan^(−1) (((2x+1)/( (√3))))−(4/( (√3)))tan^(−1) (((2x−1)/( (√3)))) =((10x^3 +2x)/((x^2 +x+1)(x^2 −x+1)))+2ln((x^2 −x+1)/(x^2 +x+1)) −(2/(3(√3)))[tan^(−1) (((2x−1)/( (√3))))+tan^(−1) (((2x+1)/( (√3))))] It is easy to see that 4F(0)=0 4F(+∞)=−(2/(3(√3)))((π/2)+(π/2))=−((2π)/(3(√3))) Therefore,∫_0 ^(+∞) ((2x^2 −1)/((x^2 +x+1)^2 (x^2 −x+1)^2 ))dx=((−2𝛑)/(3(√3)))](https://www.tinkutara.com/question/Q105299.png)
$$ \\ $$$$\mathrm{F}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{4x}^{\mathrm{2}} }{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}−\int\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }=\int\left(\mathrm{A}\right)+\int\left(\mathrm{B}\right) \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{B}=\:\frac{\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }=\left[\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{x}+\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)}−\frac{\mathrm{x}−\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)}\right)\right]^{\mathrm{2}} =\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{1}}{\mathrm{4}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{1}}{\mathrm{4}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{2x}^{\mathrm{2}} −\mathrm{2}}{\mathrm{4}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)}+\frac{\mathrm{x}}{\mathrm{4}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{4}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)}+\frac{−\mathrm{x}}{\mathrm{4}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{2x}+\mathrm{1}}{\mathrm{4}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)}−\frac{\mathrm{2x}−\mathrm{1}}{\mathrm{4}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)} \\ $$$$\frac{\mathrm{2x}+\mathrm{2}}{\mathrm{4}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)}−\frac{\mathrm{2x}−\mathrm{2}}{\mathrm{4}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)}+\frac{\mathrm{x}}{\mathrm{4}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{−\mathrm{x}}{\mathrm{4}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\left(\mathrm{set}\:\begin{cases}{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}=\mathrm{u}}\\{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}=\mathrm{v}}\end{cases}\:\right) \\ $$$$\mathrm{4B}=\frac{\mathrm{x}}{\mathrm{u}^{\mathrm{2}} }−\frac{\mathrm{x}}{\mathrm{v}^{\mathrm{2}} }+\frac{\mathrm{2x}+\mathrm{2}}{\mathrm{u}}−\frac{\mathrm{2x}−\mathrm{2}}{\mathrm{v}} \\ $$$$\mathrm{A}=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}\right)^{\mathrm{2}} =\left(\frac{\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{2}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)}\right)\mathrm{dx} \\ $$$$\mathrm{2A}=\frac{\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }+\left(\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}}−\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{u}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{v}^{\mathrm{2}} }+\frac{\mathrm{x}−\mathrm{1}}{\mathrm{v}}−\frac{\mathrm{x}+\mathrm{1}}{\mathrm{u}} \\ $$$$\Rightarrow\mathrm{4A}=\frac{\mathrm{2}}{\mathrm{u}^{\mathrm{2}} }+\frac{\mathrm{2}}{\mathrm{v}^{\mathrm{2}} }+\frac{\mathrm{2x}−\mathrm{2}}{\mathrm{v}}−\frac{\mathrm{2x}+\mathrm{2}}{\mathrm{u}}.\mathrm{Hence}, \\ $$$$\mathrm{4F}=\mathrm{4A}−\mathrm{4B}=−\frac{\mathrm{x}−\mathrm{2}}{\mathrm{u}^{\mathrm{2}} }+\frac{\mathrm{x}+\mathrm{2}}{\mathrm{v}^{\mathrm{2}} }−\frac{\left.\mathrm{4x}+\mathrm{1}\right)}{\mathrm{u}}+\frac{\mathrm{4}\left(\mathrm{x}−\mathrm{1}\right)}{\mathrm{v}} \\ $$$$\mathrm{4F}=\int\left(−\frac{\mathrm{x}−\mathrm{2}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{x}+\mathrm{2}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }−\frac{\left.\mathrm{4x}+\mathrm{1}\right)}{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}+\frac{\mathrm{4}\left(\mathrm{x}−\mathrm{1}\right)}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}}\right)\mathrm{dx} \\ $$$$\mathrm{We}\:\mathrm{have}:\int\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}=\int\frac{\mathrm{d}\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)}{\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} }=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}}{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\right) \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\left(\mathrm{as}\:\int\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} \right)}=\frac{\mathrm{1}}{\mathrm{a}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{x}}{\mathrm{a}}\right)\right) \\ $$$$\mathrm{Consequently}, \\ $$$$\mathrm{M}=\int\frac{\mathrm{x}−\mathrm{2}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2x}+\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{5}}{\mathrm{2}}\int\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{d}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{3}}{\mathrm{2}}\mathrm{I}_{\mathrm{2}} =−\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{I}_{\mathrm{2}} \\ $$$$\mathrm{N}=\int\frac{\mathrm{x}+\mathrm{2}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2x}−\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$+\frac{\mathrm{5}}{\mathrm{2}}\int\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }=−\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{5}}{\mathrm{2}}.\mathrm{J}_{\mathrm{2}} \\ $$$$\mathrm{P}=\int\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}\mathrm{dx}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2x}+\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}\mathrm{dx}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right) \\ $$$$\mathrm{Q}=\int\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}}\mathrm{dx}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2x}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right) \\ $$$$\mathrm{We}\:\mathrm{have}:\mathrm{I}_{\mathrm{2}} =\int\frac{\mathrm{dt}}{\left(\mathrm{t}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} \right)^{\mathrm{2}} }\left(\mathrm{with}\:\mathrm{t}=\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right. \\ $$$$\mathrm{Apply}\:\mathrm{current}\:\mathrm{formular}\::\mathrm{I}_{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{2a}^{\mathrm{2}} \left(\mathrm{n}−\mathrm{1}\right)}.\frac{\mathrm{t}}{\left(\mathrm{t}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} \right)^{\mathrm{n}−\mathrm{1}} }+\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} }.\frac{\mathrm{2n}−\mathrm{3}}{\mathrm{2n}−\mathrm{2}}.\mathrm{I}_{\mathrm{n}−\mathrm{1}} \mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{I}_{\mathrm{2}} =\frac{\mathrm{2}}{\mathrm{3}}.\frac{\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}}{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}+\frac{\mathrm{4}}{\mathrm{3}}.\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{d}\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)}{\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{2x}+\mathrm{1}}{\mathrm{3}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)}+.\frac{\mathrm{4}}{\mathrm{3}\sqrt{\mathrm{3}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right).\mathrm{Similarly}, \\ $$$$\mathrm{J}_{\mathrm{2}} =\frac{\mathrm{2x}−\mathrm{1}}{\mathrm{3}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)}+\frac{\mathrm{4}}{\mathrm{3}\sqrt{\mathrm{3}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2x}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right) \\ $$$$\mathrm{Finally},\mathrm{4F}=−\mathrm{M}+\mathrm{N}−\mathrm{4P}+\mathrm{4Q}=\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)} \\ $$$$+\frac{\mathrm{5}}{\mathrm{2}}\left\{\frac{\mathrm{2x}+\mathrm{1}}{\mathrm{3}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)}+.\frac{\mathrm{4}}{\mathrm{3}\sqrt{\mathrm{3}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\right. \\ $$$$\left.+\left[\frac{\mathrm{2x}−\mathrm{1}}{\mathrm{3}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)}+\frac{\mathrm{4}}{\mathrm{3}\sqrt{\mathrm{3}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2x}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\right]\:\right\} \\ $$$$−\mathrm{2ln}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)+\mathrm{2ln}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)−\frac{\mathrm{4}}{\:\sqrt{\mathrm{3}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)−\frac{\mathrm{4}}{\:\sqrt{\mathrm{3}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2x}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right) \\ $$$$=\frac{\mathrm{10x}^{\mathrm{3}} +\mathrm{2x}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)}+\mathrm{2ln}\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}} \\ $$$$−\frac{\mathrm{2}}{\mathrm{3}\sqrt{\mathrm{3}}}\left[\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2x}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)+\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\right] \\ $$$$\mathrm{It}\:\mathrm{is}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{see}\:\mathrm{that}\:\mathrm{4F}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$$\mathrm{4F}\left(+\infty\right)=−\frac{\mathrm{2}}{\mathrm{3}\sqrt{\mathrm{3}}}\left(\frac{\pi}{\mathrm{2}}+\frac{\pi}{\mathrm{2}}\right)=−\frac{\mathrm{2}\pi}{\mathrm{3}\sqrt{\mathrm{3}}} \\ $$$$\mathrm{Th}\boldsymbol{\mathrm{erefore}},\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{2}\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\mathrm{1}}{\left(\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\boldsymbol{\mathrm{x}}+\mathrm{1}\right)^{\mathrm{2}} \left(\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\boldsymbol{\mathrm{x}}+\mathrm{1}\right)^{\mathrm{2}} }\boldsymbol{\mathrm{dx}}=\frac{−\mathrm{2}\boldsymbol{\pi}}{\mathrm{3}\sqrt{\mathrm{3}}} \\ $$
Commented by abdomathmax last updated on 27/Jul/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}. \\ $$
