Menu Close

calculate-0-4pi-dx-2-cosx-2-

Tinku Tara 0 Comments
Pin




Question Number 144241 by mathmax by abdo last updated on 23/Jun/21
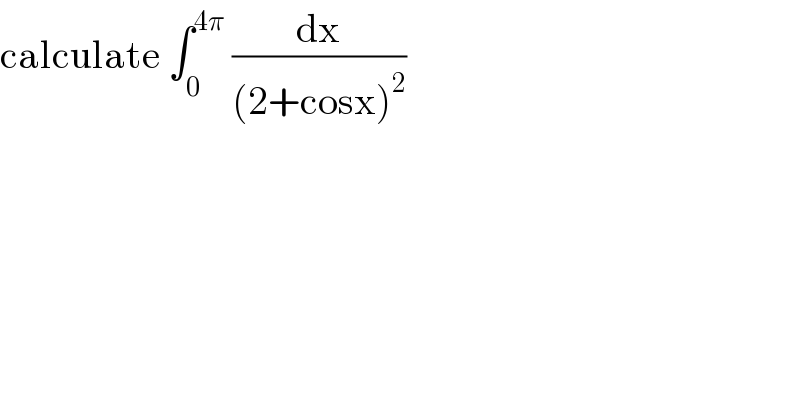
calculate ∫_0 ^(4π) (dx/((2+cosx)^2 ))
$$\mathrm{calculate}\:\int_{\mathrm{0}} ^{\mathrm{4}\pi} \:\frac{\mathrm{dx}}{\left(\mathrm{2}+\mathrm{cosx}\right)^{\mathrm{2}} } \\ $$
Answered by Ar Brandon last updated on 05/Jul/21
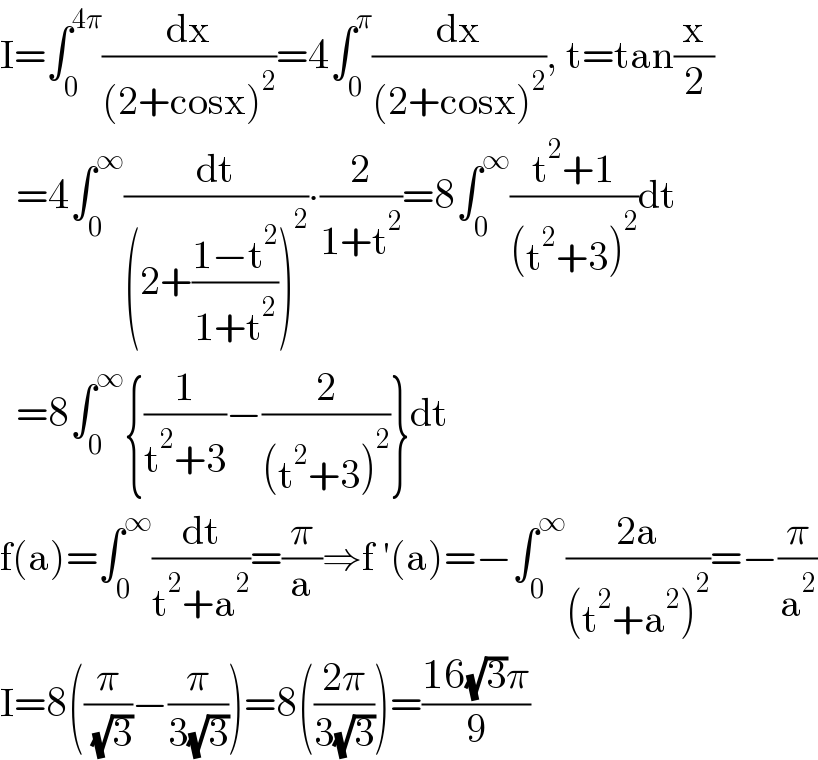
I=∫_0 ^(4π) (dx/((2+cosx)^2 ))=4∫_0 ^π (dx/((2+cosx)^2 )), t=tan(x/2) =4∫_0 ^∞ (dt/((2+((1−t^2 )/(1+t^2 )))^2 ))∙(2/(1+t^2 ))=8∫_0 ^∞ ((t^2 +1)/((t^2 +3)^2 ))dt =8∫_0 ^∞ {(1/(t^2 +3))−(2/((t^2 +3)^2 ))}dt f(a)=∫_0 ^∞ (dt/(t^2 +a^2 ))=(π/a)⇒f ′(a)=−∫_0 ^∞ ((2a)/((t^2 +a^2 )^2 ))=−(π/a^2 ) I=8((π/( (√3)))−(π/(3(√3))))=8(((2π)/(3(√3))))=((16(√3)π)/9)
$$\mathrm{I}=\int_{\mathrm{0}} ^{\mathrm{4}\pi} \frac{\mathrm{dx}}{\left(\mathrm{2}+\mathrm{cosx}\right)^{\mathrm{2}} }=\mathrm{4}\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{dx}}{\left(\mathrm{2}+\mathrm{cosx}\right)^{\mathrm{2}} },\:\mathrm{t}=\mathrm{tan}\frac{\mathrm{x}}{\mathrm{2}} \\ $$$$\:\:=\mathrm{4}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{dt}}{\left(\mathrm{2}+\frac{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\right)^{\mathrm{2}} }\centerdot\frac{\mathrm{2}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }=\mathrm{8}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}{\left(\mathrm{t}^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{2}} }\mathrm{dt} \\ $$$$\:\:=\mathrm{8}\int_{\mathrm{0}} ^{\infty} \left\{\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} +\mathrm{3}}−\frac{\mathrm{2}}{\left(\mathrm{t}^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{2}} }\right\}\mathrm{dt} \\ $$$$\mathrm{f}\left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} }=\frac{\pi}{\mathrm{a}}\Rightarrow\mathrm{f}\:'\left(\mathrm{a}\right)=−\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{2a}}{\left(\mathrm{t}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} \right)^{\mathrm{2}} }=−\frac{\pi}{\mathrm{a}^{\mathrm{2}} } \\ $$$$\mathrm{I}=\mathrm{8}\left(\frac{\pi}{\:\sqrt{\mathrm{3}}}−\frac{\pi}{\mathrm{3}\sqrt{\mathrm{3}}}\right)=\mathrm{8}\left(\frac{\mathrm{2}\pi}{\mathrm{3}\sqrt{\mathrm{3}}}\right)=\frac{\mathrm{16}\sqrt{\mathrm{3}}\pi}{\mathrm{9}} \\ $$
Answered by mathmax by abdo last updated on 25/Jun/21
let f(a)=∫_0 ^(4π) (dx/(a+cosx)) with a>1 ⇒f^′ (a)=−∫_0 ^(4π) (dx/((a+cosx)^2 )) ⇒ −f^′ (2)=∫_0 ^(4π) (dx/((2+cosx)^2 )) we have f(a)=∫_0 ^(2π) (dx/(a+cosx))+∫_(2π) ^(4π) (dx/(a+cosx))(→x=2π+t) =2∫_0 ^(2π) (dx/(a+cosx))=_(e^(ix) =z) 2∫_(∣z∣=1) (dz/(iz(a+((z+z^(−1) )/2)))) =4∫_(∣z∣=1) ((−idz)/(z(2a+z+z^(−1) )))=−4i∫_(∣z∣=1) (dz/(2az+z^2 +1)) ϕ(z)=(1/(z^2 +2az +1)) Δ^′ =a^2 −1>0 ⇒z_1 =−a+(√(a^2 −1)) and z_2 =−a−(√(a^2 −1)) ∣z_1 ∣−1 =∣(√(a^2 −1))−a∣−1 =a−(√(a^2 −1))−1 ⇒ϕ(z)=(1/((z−z_1 )(z−z_2 ))) =a−1−(√(a^2 −1)) and (a−1)^2 −a^2 +1 =a^2 −2a+1−a^2 +1 =2−2a =2(1−a)<0 and ∣z_2 ∣−1 =a+(√(a^2 −1))−1>0 ⇒ ∫_R ϕ(z)dz =2iπRes(ϕ,z_1 )=2iπ×(1/(z_1 −z_2 ))=((2iπ)/(2(√(a^2 −1)))) =((iπ)/( (√(a^2 −1)))) ⇒ f(a)=(−4i)×((iπ)/( (√(a^2 −1))))=((4π)/( (√(a^2 −1)))) =4π(a^2 −1)^(−(1/2)) ⇒ f^′ (a)=−2π(2a)(a^2 −1)^(−(3/2)) =((−4πa)/((a^2 −1)(√(a^2 −1)))) ⇒ f^′ (2)=((−8π)/(3(√3))) ⇒∫_0 ^(4π) (dx/((2+cosx)^2 ))=((8π)/(3(√3)))
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\mathrm{4}\pi} \:\frac{\mathrm{dx}}{\mathrm{a}+\mathrm{cosx}}\:\:\:\mathrm{with}\:\mathrm{a}>\mathrm{1}\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{a}\right)=−\int_{\mathrm{0}} ^{\mathrm{4}\pi} \:\frac{\mathrm{dx}}{\left(\mathrm{a}+\mathrm{cosx}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$−\mathrm{f}^{'} \left(\mathrm{2}\right)=\int_{\mathrm{0}} ^{\mathrm{4}\pi} \:\frac{\mathrm{dx}}{\left(\mathrm{2}+\mathrm{cosx}\right)^{\mathrm{2}} }\:\mathrm{we}\:\mathrm{have}\:\mathrm{f}\left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\frac{\mathrm{dx}}{\mathrm{a}+\mathrm{cosx}}+\int_{\mathrm{2}\pi} ^{\mathrm{4}\pi} \:\frac{\mathrm{dx}}{\mathrm{a}+\mathrm{cosx}}\left(\rightarrow\mathrm{x}=\mathrm{2}\pi+\mathrm{t}\right) \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\frac{\mathrm{dx}}{\mathrm{a}+\mathrm{cosx}}=_{\mathrm{e}^{\mathrm{ix}} \:=\mathrm{z}} \:\:\mathrm{2}\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\:\:\frac{\mathrm{dz}}{\mathrm{iz}\left(\mathrm{a}+\frac{\mathrm{z}+\mathrm{z}^{−\mathrm{1}} }{\mathrm{2}}\right)} \\ $$$$=\mathrm{4}\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\:\frac{−\mathrm{idz}}{\mathrm{z}\left(\mathrm{2a}+\mathrm{z}+\mathrm{z}^{−\mathrm{1}} \right)}=−\mathrm{4i}\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\:\frac{\mathrm{dz}}{\mathrm{2az}+\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$\varphi\left(\mathrm{z}\right)=\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{2}} \:+\mathrm{2az}\:+\mathrm{1}} \\ $$$$\Delta^{'} \:=\mathrm{a}^{\mathrm{2}} −\mathrm{1}>\mathrm{0}\:\Rightarrow\mathrm{z}_{\mathrm{1}} =−\mathrm{a}+\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{1}}\:\mathrm{and}\:\mathrm{z}_{\mathrm{2}} =−\mathrm{a}−\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\mid\mathrm{z}_{\mathrm{1}} \mid−\mathrm{1}\:=\mid\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{1}}−\mathrm{a}\mid−\mathrm{1}\:=\mathrm{a}−\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{1}}−\mathrm{1}\:\Rightarrow\varphi\left(\mathrm{z}\right)=\frac{\mathrm{1}}{\left(\mathrm{z}−\mathrm{z}_{\mathrm{1}} \right)\left(\mathrm{z}−\mathrm{z}_{\mathrm{2}} \right)} \\ $$$$=\mathrm{a}−\mathrm{1}−\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{1}}\:\mathrm{and}\:\left(\mathrm{a}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} \:+\mathrm{1}\:=\mathrm{a}^{\mathrm{2}} −\mathrm{2a}+\mathrm{1}−\mathrm{a}^{\mathrm{2}} \:+\mathrm{1} \\ $$$$=\mathrm{2}−\mathrm{2a}\:=\mathrm{2}\left(\mathrm{1}−\mathrm{a}\right)<\mathrm{0}\:\:\mathrm{and}\:\mid\mathrm{z}_{\mathrm{2}} \mid−\mathrm{1}\:=\mathrm{a}+\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{1}}−\mathrm{1}>\mathrm{0}\:\Rightarrow \\ $$$$\int_{\mathrm{R}} \varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\mathrm{Res}\left(\varphi,\mathrm{z}_{\mathrm{1}} \right)=\mathrm{2i}\pi×\frac{\mathrm{1}}{\mathrm{z}_{\mathrm{1}} −\mathrm{z}_{\mathrm{2}} }=\frac{\mathrm{2i}\pi}{\mathrm{2}\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{1}}}\:=\frac{\mathrm{i}\pi}{\:\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{1}}}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{a}\right)=\left(−\mathrm{4i}\right)×\frac{\mathrm{i}\pi}{\:\sqrt{\mathrm{a}^{\mathrm{2}} \:−\mathrm{1}}}=\frac{\mathrm{4}\pi}{\:\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{1}}}\:=\mathrm{4}\pi\left(\mathrm{a}^{\mathrm{2}} −\mathrm{1}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \:\Rightarrow \\ $$$$\mathrm{f}^{'} \left(\mathrm{a}\right)=−\mathrm{2}\pi\left(\mathrm{2a}\right)\left(\mathrm{a}^{\mathrm{2}} −\mathrm{1}\right)^{−\frac{\mathrm{3}}{\mathrm{2}}} \:=\frac{−\mathrm{4}\pi\mathrm{a}}{\left(\mathrm{a}^{\mathrm{2}} −\mathrm{1}\right)\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{1}}}\:\Rightarrow \\ $$$$\mathrm{f}^{'} \left(\mathrm{2}\right)=\frac{−\mathrm{8}\pi}{\mathrm{3}\sqrt{\mathrm{3}}}\:\Rightarrow\int_{\mathrm{0}} ^{\mathrm{4}\pi} \:\frac{\mathrm{dx}}{\left(\mathrm{2}+\mathrm{cosx}\right)^{\mathrm{2}} }=\frac{\mathrm{8}\pi}{\mathrm{3}\sqrt{\mathrm{3}}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *