Question Number 144214 by Mathspace last updated on 23/Jun/21
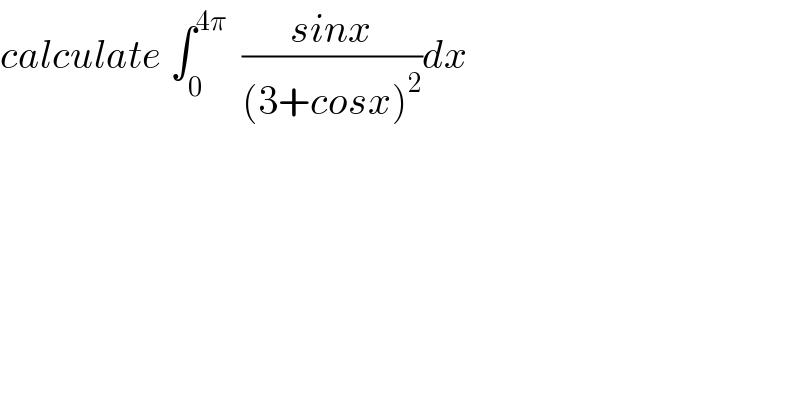
$${calculate}\:\int_{\mathrm{0}} ^{\mathrm{4}\pi} \:\:\frac{{sinx}}{\left(\mathrm{3}+{cosx}\right)^{\mathrm{2}} }{dx} \\ $$
Answered by bemath last updated on 23/Jun/21
![=−∫_0 ^(4π) ((d(3+cos x))/((3+cos x)^2 )) =−[ −(1/(3+cos x)) ]_0 ^(4π) = [(1/(3+cos 4π))]−[(1/(3+cos 0)) ] =0](https://www.tinkutara.com/question/Q144223.png)
$$=−\underset{\mathrm{0}} {\overset{\mathrm{4}\pi} {\int}}\:\frac{\mathrm{d}\left(\mathrm{3}+\mathrm{cos}\:\mathrm{x}\right)}{\left(\mathrm{3}+\mathrm{cos}\:\mathrm{x}\right)^{\mathrm{2}} } \\ $$$$=−\left[\:−\frac{\mathrm{1}}{\mathrm{3}+\mathrm{cos}\:\mathrm{x}}\:\right]_{\mathrm{0}} ^{\mathrm{4}\pi} \\ $$$$=\:\left[\frac{\mathrm{1}}{\mathrm{3}+\mathrm{cos}\:\mathrm{4}\pi}\right]−\left[\frac{\mathrm{1}}{\mathrm{3}+\mathrm{cos}\:\mathrm{0}}\:\right]\:=\mathrm{0} \\ $$
