Question Number 96195 by mathmax by abdo last updated on 30/May/20
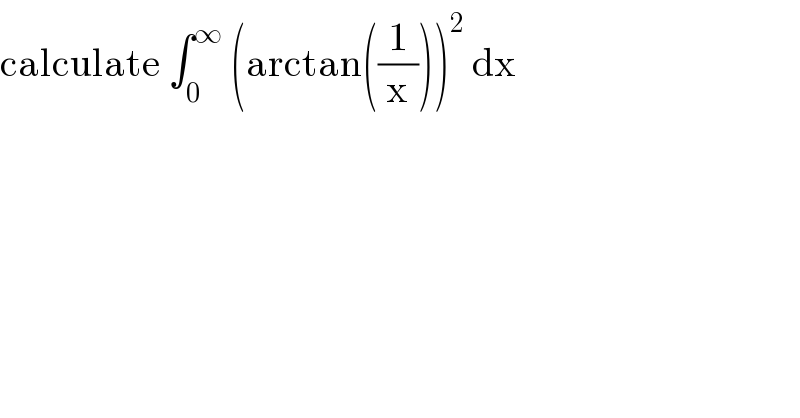
$$\mathrm{calculate}\:\int_{\mathrm{0}} ^{\infty} \:\left(\mathrm{arctan}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)\right)^{\mathrm{2}} \:\mathrm{dx} \\ $$
Answered by mathmax by abdo last updated on 01/Jun/20
![A =∫_0 ^∞ (arctan((1/x)))^2 dx changement (1/x)=t give A =−∫_0 ^∞ (arctan(t)^2 (((−dt)/t^2 ))) =∫_0 ^∞ ((arctan^2 t)/t^2 )dt =_(by parts) [−(1/t) arctan^2 t]_0 ^∞ +∫_0 ^∞ (1/t) (2arctant)×(1/(1+t^2 ))dt =0 +2 ∫_0 ^∞ ((arctant)/(t(1+t^2 )))dt =_(t =tanθ) 2 ∫_0 ^(π/2) (θ/(tanθ(1+tan^2 θ)))(1+tan^2 θ)dθ =2 ∫_0 ^(π/2) θ×((cosθ)/(sinθ))dθ by parts u =θ and v^′ =((cosθ)/(sinθ)) ⇒ A =2{ [θ ln(sinθ)]_0 ^(π/2) −∫_0 ^(π/2) ln(sinθ)dθ} =−2 ∫_0 ^(π/2) ln(sinθ)dθ =−2×(−(π/2)ln2) A=πln(2)](https://www.tinkutara.com/question/Q96474.png)
$$\mathrm{A}\:=\int_{\mathrm{0}} ^{\infty} \:\left(\mathrm{arctan}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)\right)^{\mathrm{2}} \:\mathrm{dx}\:\:\mathrm{changement}\:\frac{\mathrm{1}}{\mathrm{x}}=\mathrm{t}\:\mathrm{give} \\ $$$$\mathrm{A}\:=−\int_{\mathrm{0}} ^{\infty} \:\:\left(\mathrm{arctan}\left(\mathrm{t}\right)^{\mathrm{2}} \left(\frac{−\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} }\right)\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{arctan}^{\mathrm{2}} \mathrm{t}}{\mathrm{t}^{\mathrm{2}} }\mathrm{dt} \\ $$$$=_{\mathrm{by}\:\mathrm{parts}} \:\:\:\:\:\left[−\frac{\mathrm{1}}{\mathrm{t}}\:\mathrm{arctan}^{\mathrm{2}} \mathrm{t}\right]_{\mathrm{0}} ^{\infty} +\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{t}}\:\left(\mathrm{2arctant}\right)×\frac{\mathrm{1}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt} \\ $$$$=\mathrm{0}\:+\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{arctant}}{\mathrm{t}\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)}\mathrm{dt}\:\:=_{\mathrm{t}\:=\mathrm{tan}\theta} \:\:\:\:\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\theta}{\mathrm{tan}\theta\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta\right)}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta\right)\mathrm{d}\theta \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\theta×\frac{\mathrm{cos}\theta}{\mathrm{sin}\theta}\mathrm{d}\theta\:\:\:\mathrm{by}\:\mathrm{parts}\:\:\mathrm{u}\:=\theta\:\mathrm{and}\:\mathrm{v}^{'} \:=\frac{\mathrm{cos}\theta}{\mathrm{sin}\theta}\:\Rightarrow \\ $$$$\mathrm{A}\:=\mathrm{2}\left\{\:\:\left[\theta\:\mathrm{ln}\left(\mathrm{sin}\theta\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{ln}\left(\mathrm{sin}\theta\right)\mathrm{d}\theta\right\}\:=−\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{sin}\theta\right)\mathrm{d}\theta\:=−\mathrm{2}×\left(−\frac{\pi}{\mathrm{2}}\mathrm{ln2}\right) \\ $$$$\mathrm{A}=\pi\mathrm{ln}\left(\mathrm{2}\right) \\ $$
