Question Number 103741 by mathmax by abdo last updated on 17/Jul/20

$$\mathrm{calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{arctan}\left(\mathrm{ch}\left(\mathrm{x}\right)\right)}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{9}}\mathrm{dx} \\ $$
Answered by mathmax by abdo last updated on 17/Jul/20
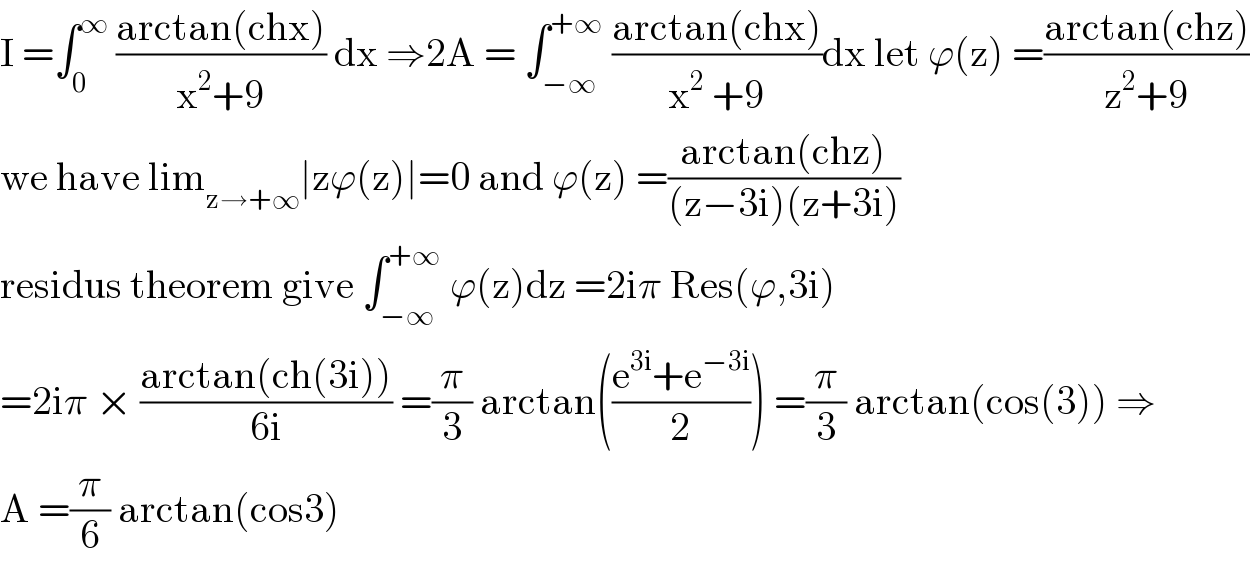
$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{arctan}\left(\mathrm{chx}\right)}{\mathrm{x}^{\mathrm{2}} +\mathrm{9}}\:\mathrm{dx}\:\Rightarrow\mathrm{2A}\:=\:\int_{−\infty} ^{+\infty} \:\frac{\mathrm{arctan}\left(\mathrm{chx}\right)}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{9}}\mathrm{dx}\:\mathrm{let}\:\varphi\left(\mathrm{z}\right)\:=\frac{\mathrm{arctan}\left(\mathrm{chz}\right)}{\mathrm{z}^{\mathrm{2}} +\mathrm{9}} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{lim}_{\mathrm{z}\rightarrow+\infty} \mid\mathrm{z}\varphi\left(\mathrm{z}\right)\mid=\mathrm{0}\:\mathrm{and}\:\varphi\left(\mathrm{z}\right)\:=\frac{\mathrm{arctan}\left(\mathrm{chz}\right)}{\left(\mathrm{z}−\mathrm{3i}\right)\left(\mathrm{z}+\mathrm{3i}\right)} \\ $$$$\mathrm{residus}\:\mathrm{theorem}\:\mathrm{give}\:\int_{−\infty} ^{+\infty} \:\varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\:\mathrm{Res}\left(\varphi,\mathrm{3i}\right) \\ $$$$=\mathrm{2i}\pi\:×\:\frac{\mathrm{arctan}\left(\mathrm{ch}\left(\mathrm{3i}\right)\right)}{\mathrm{6i}}\:=\frac{\pi}{\mathrm{3}}\:\mathrm{arctan}\left(\frac{\mathrm{e}^{\mathrm{3i}} +\mathrm{e}^{−\mathrm{3i}} }{\mathrm{2}}\right)\:=\frac{\pi}{\mathrm{3}}\:\mathrm{arctan}\left(\mathrm{cos}\left(\mathrm{3}\right)\right)\:\Rightarrow \\ $$$$\mathrm{A}\:=\frac{\pi}{\mathrm{6}}\:\mathrm{arctan}\left(\mathrm{cos3}\right) \\ $$
