Question Number 90279 by mathmax by abdo last updated on 22/Apr/20
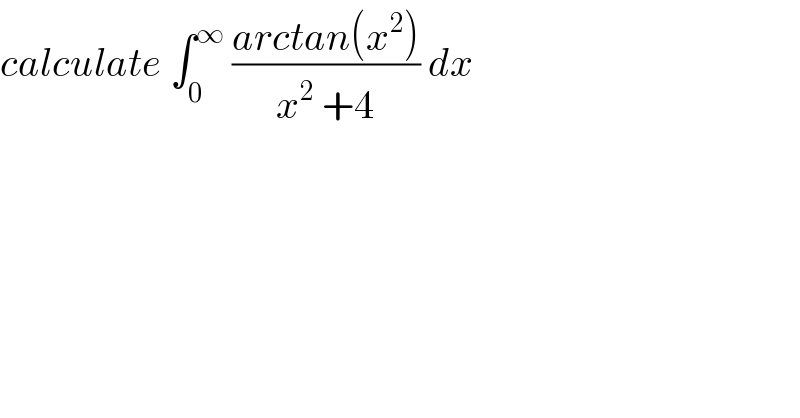
$${calculate}\:\int_{\mathrm{0}} ^{\infty} \:\frac{{arctan}\left({x}^{\mathrm{2}} \right)}{{x}^{\mathrm{2}} \:+\mathrm{4}}\:{dx} \\ $$
Commented by mathmax by abdo last updated on 23/Apr/20
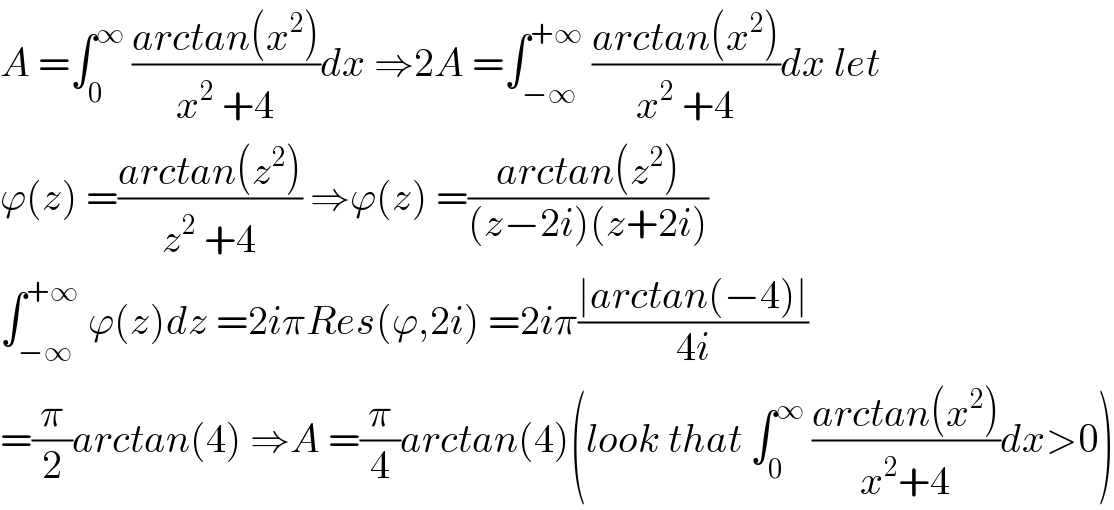
$${A}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{{arctan}\left({x}^{\mathrm{2}} \right)}{{x}^{\mathrm{2}} \:+\mathrm{4}}{dx}\:\Rightarrow\mathrm{2}{A}\:=\int_{−\infty} ^{+\infty} \:\frac{{arctan}\left({x}^{\mathrm{2}} \right)}{{x}^{\mathrm{2}} \:+\mathrm{4}}{dx}\:{let}\: \\ $$$$\varphi\left({z}\right)\:=\frac{{arctan}\left({z}^{\mathrm{2}} \right)}{{z}^{\mathrm{2}} \:+\mathrm{4}}\:\Rightarrow\varphi\left({z}\right)\:=\frac{{arctan}\left({z}^{\mathrm{2}} \right)}{\left({z}−\mathrm{2}{i}\right)\left({z}+\mathrm{2}{i}\right)} \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi{Res}\left(\varphi,\mathrm{2}{i}\right)\:=\mathrm{2}{i}\pi\frac{\mid{arctan}\left(−\mathrm{4}\right)\mid}{\mathrm{4}{i}} \\ $$$$=\frac{\pi}{\mathrm{2}}{arctan}\left(\mathrm{4}\right)\:\Rightarrow{A}\:=\frac{\pi}{\mathrm{4}}{arctan}\left(\mathrm{4}\right)\left({look}\:{that}\:\int_{\mathrm{0}} ^{\infty} \:\frac{{arctan}\left({x}^{\mathrm{2}} \right)}{{x}^{\mathrm{2}} +\mathrm{4}}{dx}>\mathrm{0}\right) \\ $$
