Question Number 54573 by Abdo msup. last updated on 07/Feb/19
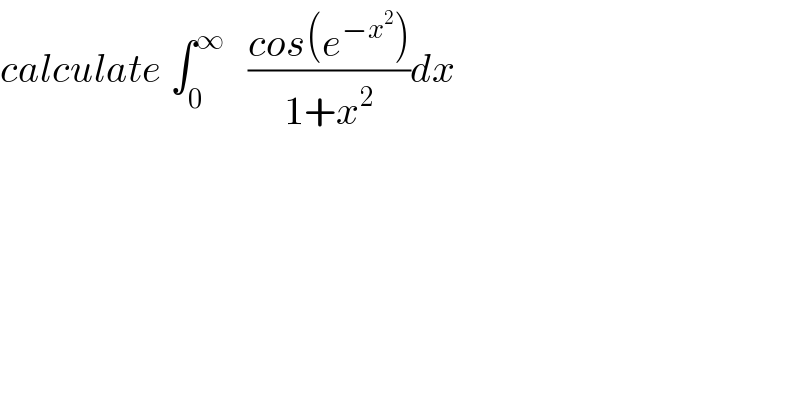
$${calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{cos}\left({e}^{−{x}^{\mathrm{2}} } \right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\: \\ $$
Commented by maxmathsup by imad last updated on 08/Feb/19
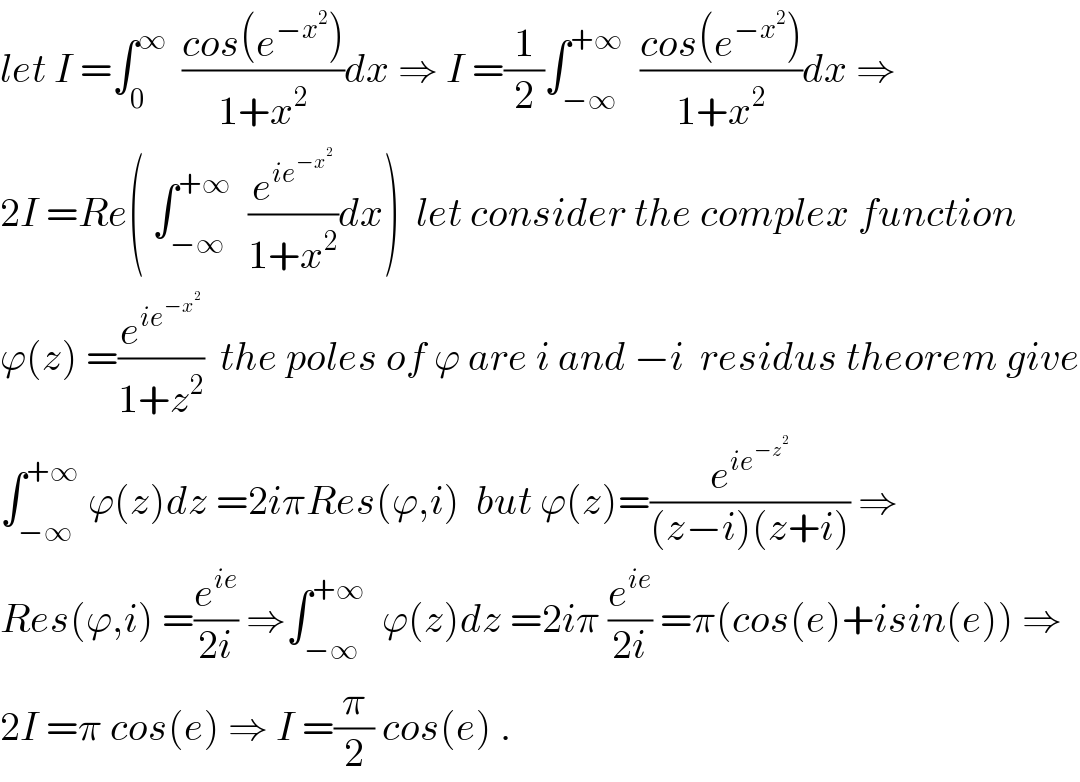
$${let}\:{I}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{cos}\left({e}^{−{x}^{\mathrm{2}} } \right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:\Rightarrow\:{I}\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{−\infty} ^{+\infty} \:\:\frac{{cos}\left({e}^{−{x}^{\mathrm{2}} } \right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:\Rightarrow \\ $$$$\mathrm{2}{I}\:={Re}\left(\:\int_{−\infty} ^{+\infty} \:\:\frac{{e}^{{ie}^{−{x}^{\mathrm{2}} } } }{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\right)\:\:{let}\:{consider}\:{the}\:{complex}\:{function}\: \\ $$$$\varphi\left({z}\right)\:=\frac{{e}^{{ie}^{−{x}^{\mathrm{2}} } } }{\mathrm{1}+{z}^{\mathrm{2}} }\:\:{the}\:{poles}\:{of}\:\varphi\:{are}\:{i}\:{and}\:−{i}\:\:{residus}\:{theorem}\:{give} \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi{Res}\left(\varphi,{i}\right)\:\:{but}\:\varphi\left({z}\right)=\frac{{e}^{{ie}^{−{z}^{\mathrm{2}} } } }{\left({z}−{i}\right)\left({z}+{i}\right)}\:\Rightarrow \\ $$$${Res}\left(\varphi,{i}\right)\:=\frac{{e}^{{ie}} }{\mathrm{2}{i}}\:\Rightarrow\int_{−\infty} ^{+\infty} \:\:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:\frac{{e}^{{ie}} }{\mathrm{2}{i}}\:=\pi\left({cos}\left({e}\right)+{isin}\left({e}\right)\right)\:\Rightarrow \\ $$$$\mathrm{2}{I}\:=\pi\:{cos}\left({e}\right)\:\Rightarrow\:{I}\:=\frac{\pi}{\mathrm{2}}\:{cos}\left({e}\right)\:. \\ $$
