Question Number 34267 by math khazana by abdo last updated on 03/May/18
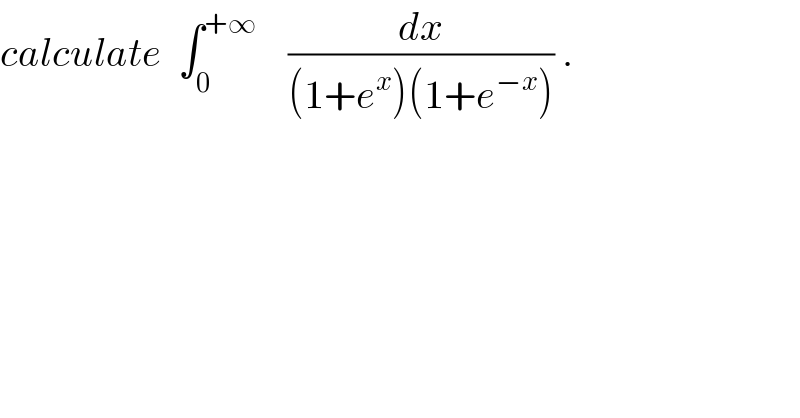
$${calculate}\:\:\int_{\mathrm{0}} ^{+\infty} \:\:\:\:\frac{{dx}}{\left(\mathrm{1}+{e}^{{x}} \right)\left(\mathrm{1}+{e}^{−{x}} \right)}\:. \\ $$
Commented by math khazana by abdo last updated on 07/May/18
![changement e^x =t give I = ∫_1 ^(+∞) (1/((1+t)(1+(1/t)))) (dt/t) = ∫_1 ^(+∞) (dt/((1+t)(t+1))) = ∫_1 ^(+∞) (dt/((t+1)^2 )) =[−(1/(t+1))]_1 ^(+∞) = (1/2) .](https://www.tinkutara.com/question/Q34527.png)
$${changement}\:\:{e}^{{x}} ={t}\:{give} \\ $$$${I}\:=\:\int_{\mathrm{1}} ^{+\infty} \:\:\:\:\frac{\mathrm{1}}{\left(\mathrm{1}+{t}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{{t}}\right)}\:\frac{{dt}}{{t}} \\ $$$$=\:\int_{\mathrm{1}} ^{+\infty} \:\:\:\:\frac{{dt}}{\left(\mathrm{1}+{t}\right)\left({t}+\mathrm{1}\right)}\:=\:\int_{\mathrm{1}} ^{+\infty} \:\:\frac{{dt}}{\left({t}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\left[−\frac{\mathrm{1}}{{t}+\mathrm{1}}\right]_{\mathrm{1}} ^{+\infty} \:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\:. \\ $$
