Question Number 51324 by Abdo msup. last updated on 25/Dec/18
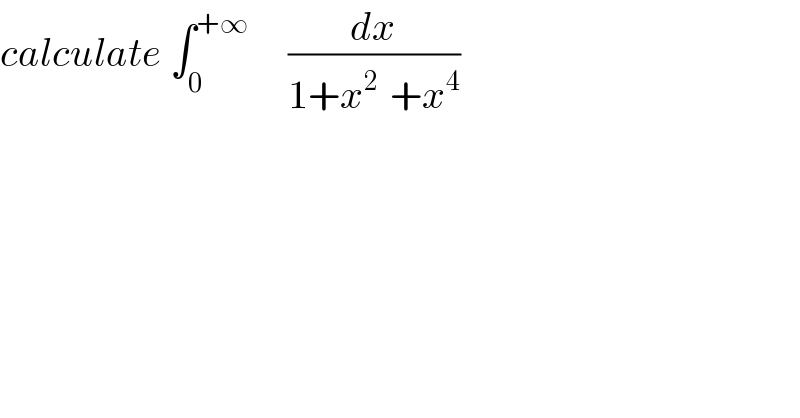
$${calculate}\:\int_{\mathrm{0}} ^{+\infty} \:\:\:\:\:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}\:} \:+{x}^{\mathrm{4}} } \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 26/Dec/18
![∫(dx/(x^4 +x^2 +1)) (1/2)∫((2/x^2 )/(x^2 +1+(1/x^2 ))) (1/2)∫(((1+(1/x^2 ))−(1−(1/x^2 )))/((x^2 +(1/x^2 )+1)))dx (1/2)∫((d(x−(1/x)))/((x−(1/x))^2 +3))−(1/2)∫((d(x+(1/x)))/((x+(1/x))^2 −1)) (1/2)×(1/( (√3)))tan^(−1) (((x−(1/x))/( (√3))))−(1/2)×(1/2)ln(((x+(1/x)−1)/(x+(1/x)+1)))+c_1 =(1/(2(√3)))×tan^(−1) (((x^2 −1)/(x(√3))))−(1/4)ln(((x^2 −x+1)/(x^2 +x+1)))+c_1 required answer =∣(1/(2(√3)))tan^(−1) (((x^2 −1)/(x(√3))))−(1/4)ln(((1−(1/x)+(1/x^2 ))/(1+(1/x)+(1/x^2 ))))∣_0 ^∞ =∣(1/(2(√3)))tan^(−1) (((1−(1/x^2 ))/((√3)/x)))−do∣_0 ^∞ =(1/(2(√3)))[tan^(−1) (((1−0)/0))−tan^(−1) (((0^2 −1)/(0×(√3))))]−(1/4)[ln(((1−0+0)/(1+0+0)))−ln(((0^2 −0+1)/(0^2 +0+1)))] =(1/(2(√3)))[tan(∞)−tan^(−1) (−∞)]−do =(1/(2(√3)))[(π/2)−(((−π)/2))] =(π/(2(√3)))](https://www.tinkutara.com/question/Q51336.png)
$$\int\frac{{dx}}{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\frac{\mathrm{2}}{{x}^{\mathrm{2}} }}{{x}^{\mathrm{2}} +\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\left(\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)−\left(\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)}{\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\mathrm{1}\right)}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left({x}−\frac{\mathrm{1}}{{x}}\right)}{\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left({x}+\frac{\mathrm{1}}{{x}}\right)}{\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} −\mathrm{1}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}{tan}^{−\mathrm{1}} \left(\frac{{x}−\frac{\mathrm{1}}{{x}}}{\:\sqrt{\mathrm{3}}}\right)−\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{{x}+\frac{\mathrm{1}}{{x}}−\mathrm{1}}{{x}+\frac{\mathrm{1}}{{x}}+\mathrm{1}}\right)+{c}_{\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}×{tan}^{−\mathrm{1}} \left(\frac{{x}^{\mathrm{2}} −\mathrm{1}}{{x}\sqrt{\mathrm{3}}}\right)−\frac{\mathrm{1}}{\mathrm{4}}{ln}\left(\frac{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}\right)+{c}_{\mathrm{1}} \\ $$$${required}\:{answer} \\ $$$$=\mid\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}{tan}^{−\mathrm{1}} \left(\frac{{x}^{\mathrm{2}} −\mathrm{1}}{{x}\sqrt{\mathrm{3}}}\right)−\frac{\mathrm{1}}{\mathrm{4}}{ln}\left(\frac{\mathrm{1}−\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{\mathrm{1}+\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}\right)\mid_{\mathrm{0}} ^{\infty} \\ $$$$=\mid\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{\frac{\sqrt{\mathrm{3}}}{{x}}}\right)−{do}\mid_{\mathrm{0}} ^{\infty} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\left[{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}−\mathrm{0}}{\mathrm{0}}\right)−{tan}^{−\mathrm{1}} \left(\frac{\mathrm{0}^{\mathrm{2}} −\mathrm{1}}{\mathrm{0}×\sqrt{\mathrm{3}}}\right)\right]−\frac{\mathrm{1}}{\mathrm{4}}\left[{ln}\left(\frac{\mathrm{1}−\mathrm{0}+\mathrm{0}}{\mathrm{1}+\mathrm{0}+\mathrm{0}}\right)−{ln}\left(\frac{\mathrm{0}^{\mathrm{2}} −\mathrm{0}+\mathrm{1}}{\mathrm{0}^{\mathrm{2}} +\mathrm{0}+\mathrm{1}}\right)\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\left[{tan}\left(\infty\right)−{tan}^{−\mathrm{1}} \left(−\infty\right)\right]−{do} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\left[\frac{\pi}{\mathrm{2}}−\left(\frac{−\pi}{\mathrm{2}}\right)\right] \\ $$$$=\frac{\pi}{\mathrm{2}\sqrt{\mathrm{3}}} \\ $$$$ \\ $$
Commented by peter frank last updated on 26/Dec/18
$${nice}\:{work}\:{sir} \\ $$
Answered by Smail last updated on 26/Dec/18
![(1/((x^2 +x+1)(x^2 −x+1)))=((ax+b)/(x^2 +x+1))+((cx+d)/(x^2 −x+1)) a=−c , d=1−b b=1−a a=b=−c=d=(1/2) A=∫_0 ^∞ (dx/(1+x^2 +x^4 ))=(1/2)∫_0 ^∞ ((x+1)/(x^2 +x+1))dx−(1/2)∫_0 ^∞ ((x−1)/(x^2 −x+1))dx =(1/4)∫_0 ^∞ ((2x+1+1)/(x^2 +x+1))dx−(1/4)∫_0 ^∞ ((2x−1−1)/(x^2 −x+1))dx =(1/4)[ln∣((x^2 +x+1)/(x^2 −x+1))∣]_0 ^∞ +(1/4)∫_0 ^∞ (dx/((x+(1/2))^2 +(3/4)))+(1/4)∫_0 ^∞ (dx/((x−(1/2))^2 +(3/4))) =(1/3)∫_0 ^∞ (dx/((((2x+1)/( (√3))))^2 +1))+(1/3)∫_0 ^∞ (dx/((((2x−1)/( (√3))))^2 +1)) t=((2x+_− 1)/( (√3)))⇒dx=((√3)/2)dt A=(1/(2(√3)))∫_(1/(√3)) ^∞ (dt/(t^2 +1))+(1/(2(√3)))∫_(−1/(√3)) ^∞ (dt/(t^2 +1)) =(1/(2(√3)))[tan^(−1) (t)]_(1/(√3)) ^∞ +(1/(2(√3)))[tan^(−1) (t)]_(−1/(√3)) ^∞ =(1/(2(√3)))((π/2)−tan^(−1) (((√3)/3)))+(1/(2(√3)))((π/2)+tan^(−1) (((√3)/3))) =(π/(2(√3)))](https://www.tinkutara.com/question/Q51349.png)
$$\frac{\mathrm{1}}{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)}=\frac{{ax}+{b}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}+\frac{{cx}+{d}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}} \\ $$$${a}=−{c}\:\:,\:\:{d}=\mathrm{1}−{b} \\ $$$${b}=\mathrm{1}−{a} \\ $$$${a}={b}=−{c}={d}=\frac{\mathrm{1}}{\mathrm{2}}\: \\ $$$${A}=\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} +{x}^{\mathrm{4}} }=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{{x}+\mathrm{1}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{dx}−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{{x}−\mathrm{1}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{2}{x}+\mathrm{1}+\mathrm{1}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{dx}−\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{2}{x}−\mathrm{1}−\mathrm{1}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left[{ln}\mid\frac{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}\mid\right]_{\mathrm{0}} ^{\infty} +\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}}+\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{\left(\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} +\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} +\mathrm{1}} \\ $$$${t}=\frac{\mathrm{2}{x}\underset{−} {+}\mathrm{1}}{\:\sqrt{\mathrm{3}}}\Rightarrow{dx}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{dt} \\ $$$${A}=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\int_{\mathrm{1}/\sqrt{\mathrm{3}}} ^{\infty} \frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\int_{−\mathrm{1}/\sqrt{\mathrm{3}}} ^{\infty} \frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\left[{tan}^{−\mathrm{1}} \left({t}\right)\right]_{\mathrm{1}/\sqrt{\mathrm{3}}} ^{\infty} +\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\left[{tan}^{−\mathrm{1}} \left({t}\right)\right]_{−\mathrm{1}/\sqrt{\mathrm{3}}} ^{\infty} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\left(\frac{\pi}{\mathrm{2}}−{tan}^{−\mathrm{1}} \left(\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\right)\right)+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\left(\frac{\pi}{\mathrm{2}}+{tan}^{−\mathrm{1}} \left(\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\right)\right) \\ $$$$=\frac{\pi}{\mathrm{2}\sqrt{\mathrm{3}}} \\ $$
Commented by peter frank last updated on 26/Dec/18
$${nice}\:{work}\:{sir} \\ $$
