Question Number 32362 by prof Abdo imad last updated on 23/Mar/18
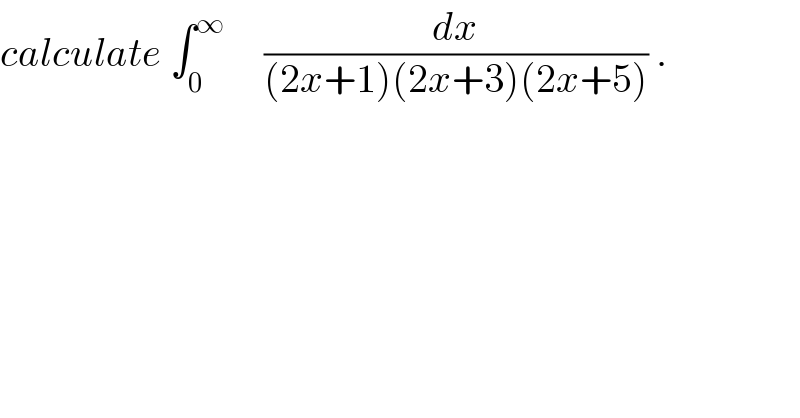
$${calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\frac{{dx}}{\left(\mathrm{2}{x}+\mathrm{1}\right)\left(\mathrm{2}{x}+\mathrm{3}\right)\left(\mathrm{2}{x}+\mathrm{5}\right)}\:. \\ $$
Answered by Joel578 last updated on 24/Mar/18
![I = ∫_0 ^∞ (dx/((2x + 1)(2x +3)(2x + 5))) = lim_(n→∞) [∫_0 ^n (1/8)((1/(2x + 1)) − (2/(2x +3)) + (1/(2x + 5))) dx] = (1/8)lim_(n→∞) [(1/2)ln (2x + 1) − ln (2x + 3) + (1/2)ln (2x + 5 )]_0 ^n = (1/(16)) lim_(n→∞) [ln (2x +1) − ln (2x + 3)^2 + ln (2x + 5)]_0 ^n = (1/(16)) lim_(n→∞) [ln (1 − (4/(4x^2 + 12x + 9)))]_0 ^n = (1/(16)) lim_(n→∞) [ln (1 − (4/(4n^2 + 12n + 9))) − ln ((5/9))] = (1/(16))(0 − ln ((5/9))) = −(1/(16)) (ln 5 − ln 9)](https://www.tinkutara.com/question/Q32377.png)
$${I}\:=\:\int_{\mathrm{0}} ^{\infty} \:\frac{{dx}}{\left(\mathrm{2}{x}\:+\:\mathrm{1}\right)\left(\mathrm{2}{x}\:+\mathrm{3}\right)\left(\mathrm{2}{x}\:+\:\mathrm{5}\right)} \\ $$$$\:\:\:\:=\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\left[\int_{\mathrm{0}} ^{{n}} \:\frac{\mathrm{1}}{\mathrm{8}}\left(\frac{\mathrm{1}}{\mathrm{2}{x}\:+\:\mathrm{1}}\:−\:\frac{\mathrm{2}}{\mathrm{2}{x}\:+\mathrm{3}}\:+\:\frac{\mathrm{1}}{\mathrm{2}{x}\:+\:\mathrm{5}}\right)\:{dx}\right] \\ $$$$\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{8}}\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\left[\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left(\mathrm{2}{x}\:+\:\mathrm{1}\right)\:−\:\mathrm{ln}\:\left(\mathrm{2}{x}\:+\:\mathrm{3}\right)\:+\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left(\mathrm{2}{x}\:+\:\mathrm{5}\:\right)\right]_{\mathrm{0}} ^{{n}} \: \\ $$$$\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{16}}\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\left[\mathrm{ln}\:\left(\mathrm{2}{x}\:+\mathrm{1}\right)\:−\:\mathrm{ln}\:\left(\mathrm{2}{x}\:+\:\mathrm{3}\right)^{\mathrm{2}} \:+\:\mathrm{ln}\:\left(\mathrm{2}{x}\:+\:\mathrm{5}\right)\right]_{\mathrm{0}} ^{{n}} \\ $$$$\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{16}}\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\left[\mathrm{ln}\:\left(\mathrm{1}\:−\:\frac{\mathrm{4}}{\mathrm{4}{x}^{\mathrm{2}} \:+\:\mathrm{12}{x}\:+\:\mathrm{9}}\right)\right]_{\mathrm{0}} ^{{n}} \\ $$$$\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{16}}\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\left[\mathrm{ln}\:\left(\mathrm{1}\:−\:\frac{\mathrm{4}}{\mathrm{4}{n}^{\mathrm{2}} \:+\:\mathrm{12}{n}\:+\:\mathrm{9}}\right)\:−\:\mathrm{ln}\:\left(\frac{\mathrm{5}}{\mathrm{9}}\right)\right] \\ $$$$\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{16}}\left(\mathrm{0}\:−\:\mathrm{ln}\:\left(\frac{\mathrm{5}}{\mathrm{9}}\right)\right) \\ $$$$\:\:\:\:=\:−\frac{\mathrm{1}}{\mathrm{16}}\:\left(\mathrm{ln}\:\mathrm{5}\:−\:\mathrm{ln}\:\mathrm{9}\right) \\ $$
