Question Number 37961 by prof Abdo imad last updated on 19/Jun/18
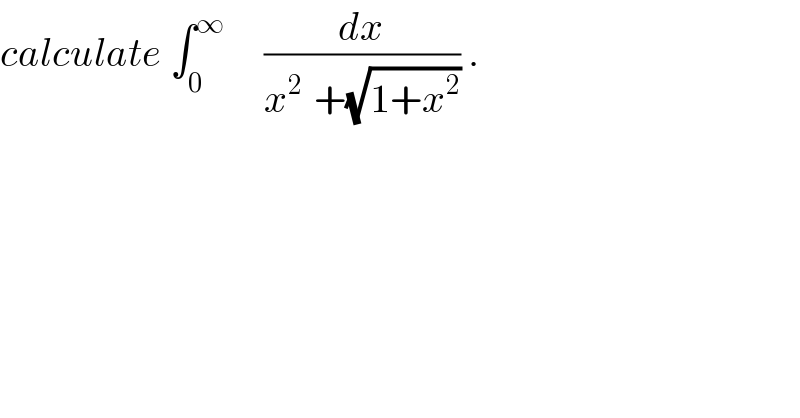
$${calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\frac{{dx}}{{x}^{\mathrm{2}\:} \:+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:. \\ $$
Answered by MJS last updated on 20/Jun/18
![∫(dx/(x^2 +(√(x^2 +1))))=∫(x^2 /(x^4 −x^2 −1))dx−∫((√(x^2 +1))/(x^4 −x^2 −1))dx= ∫(x^2 /(x^4 −x^2 −1))dx= =N_1 (∫(dx/(x−((√2)/2)(√(1+(√5)))))−∫(dx/(x+((√2)/2)(√(1+(√5))))))+N_2 ∫(dx/(x^2 −(1/2)+((√5)/2)))= =((√(10))/(20))(√(1+(√5)))ln∣((x−((√2)/2)(√(1+(√5))))/(x+((√2)/2)(√(1+(√5)))))∣+((√(10))/(10))(√(−1+(√5)))arctan(((√2)/2)(√(1+(√5)))x) ∫((√(x^2 +1))/(x^4 −x^2 −1))dx= [t=(x/( (√(x^2 +1)))) → dx=(√((x^2 +1)^3 ))dt] ∫(dt/(t^4 +t^2 −1))= =N_3 (∫(dt/(t−((√2)/2)(√(−1+(√5)))))−∫(dt/(t+((√2)/2)(√(−1+(√5))))))+N_4 ∫(dt/(t^2 +(1/2)+((√5)/2)))= =((√(10))/(20))(√(1+(√5)))ln∣((t−((√2)/2)(√(−1+(√5))))/(t+((√2)/2)(√(−1+(√5)))))∣−((√(10))/(10))(√(−1+(√5)))arctan(((√2)/2)(√(−1+(√5)))t)= =((√(10))/(20))(√(1+(√5)))ln∣(((x/( (√(x^2 +1))))−((√2)/2)(√(−1+(√5))))/((x/( (√(x^2 +1))))+((√2)/2)(√(−1+(√5)))))∣−((√(10))/(10))(√(−1+(√5)))arctan(((√2)/2)(√(−1+(√5)))(x/( (√(x^2 +1))))) =((√(10))/(20))((√(1+(√5)))(ln∣((x−((√2)/2)(√(1+(√5))))/(x+((√2)/2)(√(1+(√5)))))∣−ln∣(((x/( (√(x^2 +1))))−((√2)/2)(√(−1+(√5))))/((x/( (√(x^2 +1))))+((√2)/2)(√(−1+(√5)))))∣)+2(√(−1+(√5)))(arctan(((√2)/2)(√(1+(√5)))x)+arctan(((√2)/2)(√(−1+(√5)))(x/( (√(x^2 +1)))))))+C ∫_0 ^∞ (dx/(x^2 +(√(x^2 +1))))=((√(10))/(20))((√(1+(√5)))ln(2+(√5)+2(√(2+(√5))))+(√(−1+(√5)))(π+2arcsin(((−1+(√5))/2))))≈1.39021](https://www.tinkutara.com/question/Q37971.png)
$$\int\frac{{dx}}{{x}^{\mathrm{2}} +\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}=\int\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} −\mathrm{1}}{dx}−\int\frac{\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} −\mathrm{1}}{dx}= \\ $$$$ \\ $$$$\:\:\:\:\:\int\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} −\mathrm{1}}{dx}= \\ $$$$\:\:\:\:\:=\mathcal{N}_{\mathrm{1}} \left(\int\frac{{dx}}{{x}−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\sqrt{\mathrm{1}+\sqrt{\mathrm{5}}}}−\int\frac{{dx}}{{x}+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\sqrt{\mathrm{1}+\sqrt{\mathrm{5}}}}\right)+\mathcal{N}_{\mathrm{2}} \int\frac{{dx}}{{x}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}}= \\ $$$$\:\:\:\:\:=\frac{\sqrt{\mathrm{10}}}{\mathrm{20}}\sqrt{\mathrm{1}+\sqrt{\mathrm{5}}}\mathrm{ln}\mid\frac{{x}−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\sqrt{\mathrm{1}+\sqrt{\mathrm{5}}}}{{x}+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\sqrt{\mathrm{1}+\sqrt{\mathrm{5}}}}\mid+\frac{\sqrt{\mathrm{10}}}{\mathrm{10}}\sqrt{−\mathrm{1}+\sqrt{\mathrm{5}}}\mathrm{arctan}\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\sqrt{\mathrm{1}+\sqrt{\mathrm{5}}}{x}\right) \\ $$$$ \\ $$$$\:\:\:\:\:\int\frac{\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} −\mathrm{1}}{dx}= \\ $$$$\:\:\:\:\:\:\:\:\:\:\left[{t}=\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}\:\rightarrow\:{dx}=\sqrt{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }{dt}\right] \\ $$$$\:\:\:\:\:\int\frac{{dt}}{{t}^{\mathrm{4}} +{t}^{\mathrm{2}} −\mathrm{1}}= \\ $$$$\:\:\:\:\:=\mathcal{N}_{\mathrm{3}} \left(\int\frac{{dt}}{{t}−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\sqrt{−\mathrm{1}+\sqrt{\mathrm{5}}}}−\int\frac{{dt}}{{t}+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\sqrt{−\mathrm{1}+\sqrt{\mathrm{5}}}}\right)+\mathcal{N}_{\mathrm{4}} \int\frac{{dt}}{{t}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}}= \\ $$$$\:\:\:\:\:=\frac{\sqrt{\mathrm{10}}}{\mathrm{20}}\sqrt{\mathrm{1}+\sqrt{\mathrm{5}}}\mathrm{ln}\mid\frac{{t}−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\sqrt{−\mathrm{1}+\sqrt{\mathrm{5}}}}{{t}+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\sqrt{−\mathrm{1}+\sqrt{\mathrm{5}}}}\mid−\frac{\sqrt{\mathrm{10}}}{\mathrm{10}}\sqrt{−\mathrm{1}+\sqrt{\mathrm{5}}}\mathrm{arctan}\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\sqrt{−\mathrm{1}+\sqrt{\mathrm{5}}}{t}\right)= \\ $$$$\:\:\:\:\:=\frac{\sqrt{\mathrm{10}}}{\mathrm{20}}\sqrt{\mathrm{1}+\sqrt{\mathrm{5}}}\mathrm{ln}\mid\frac{\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\sqrt{−\mathrm{1}+\sqrt{\mathrm{5}}}}{\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\sqrt{−\mathrm{1}+\sqrt{\mathrm{5}}}}\mid−\frac{\sqrt{\mathrm{10}}}{\mathrm{10}}\sqrt{−\mathrm{1}+\sqrt{\mathrm{5}}}\mathrm{arctan}\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\sqrt{−\mathrm{1}+\sqrt{\mathrm{5}}}\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}\right) \\ $$$$ \\ $$$$=\frac{\sqrt{\mathrm{10}}}{\mathrm{20}}\left(\sqrt{\mathrm{1}+\sqrt{\mathrm{5}}}\left(\mathrm{ln}\mid\frac{{x}−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\sqrt{\mathrm{1}+\sqrt{\mathrm{5}}}}{{x}+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\sqrt{\mathrm{1}+\sqrt{\mathrm{5}}}}\mid−\mathrm{ln}\mid\frac{\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\sqrt{−\mathrm{1}+\sqrt{\mathrm{5}}}}{\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\sqrt{−\mathrm{1}+\sqrt{\mathrm{5}}}}\mid\right)+\mathrm{2}\sqrt{−\mathrm{1}+\sqrt{\mathrm{5}}}\left(\mathrm{arctan}\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\sqrt{\mathrm{1}+\sqrt{\mathrm{5}}}{x}\right)+\mathrm{arctan}\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\sqrt{−\mathrm{1}+\sqrt{\mathrm{5}}}\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}\right)\right)\right)+{C} \\ $$$$ \\ $$$$\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{{dx}}{{x}^{\mathrm{2}} +\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}=\frac{\sqrt{\mathrm{10}}}{\mathrm{20}}\left(\sqrt{\mathrm{1}+\sqrt{\mathrm{5}}}\mathrm{ln}\left(\mathrm{2}+\sqrt{\mathrm{5}}+\mathrm{2}\sqrt{\mathrm{2}+\sqrt{\mathrm{5}}}\right)+\sqrt{−\mathrm{1}+\sqrt{\mathrm{5}}}\left(\pi+\mathrm{2arcsin}\left(\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)\right)\right)\approx\mathrm{1}.\mathrm{39021} \\ $$
Commented by math khazana by abdo last updated on 20/Jun/18
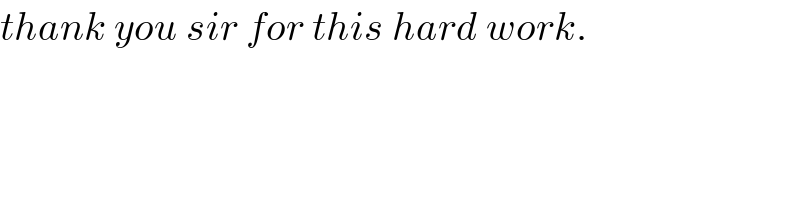
$${thank}\:{you}\:{sir}\:{for}\:{this}\:{hard}\:{work}. \\ $$
