Question Number 113203 by abdomsup last updated on 11/Sep/20
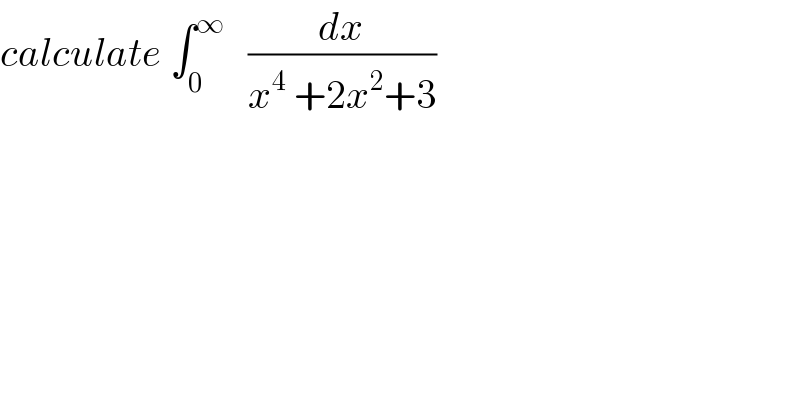
$${calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dx}}{{x}^{\mathrm{4}} \:+\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}} \\ $$
Answered by 1549442205PVT last updated on 11/Sep/20
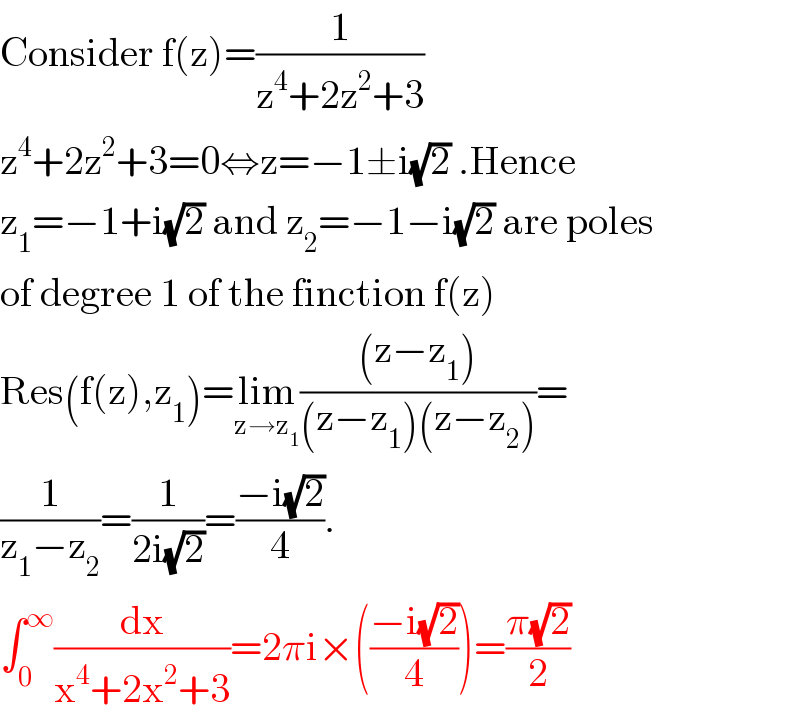
$$\mathrm{Consider}\:\mathrm{f}\left(\mathrm{z}\right)=\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{4}} +\mathrm{2z}^{\mathrm{2}} +\mathrm{3}} \\ $$$$\mathrm{z}^{\mathrm{4}} +\mathrm{2z}^{\mathrm{2}} +\mathrm{3}=\mathrm{0}\Leftrightarrow\mathrm{z}=−\mathrm{1}\pm\mathrm{i}\sqrt{\mathrm{2}}\:.\mathrm{Hence} \\ $$$$\mathrm{z}_{\mathrm{1}} =−\mathrm{1}+\mathrm{i}\sqrt{\mathrm{2}}\:\mathrm{and}\:\mathrm{z}_{\mathrm{2}} =−\mathrm{1}−\mathrm{i}\sqrt{\mathrm{2}}\:\mathrm{are}\:\mathrm{poles} \\ $$$$\mathrm{of}\:\mathrm{degree}\:\mathrm{1}\:\mathrm{of}\:\mathrm{the}\:\mathrm{finction}\:\mathrm{f}\left(\mathrm{z}\right) \\ $$$$\mathrm{Res}\left(\mathrm{f}\left(\mathrm{z}\right),\mathrm{z}_{\mathrm{1}} \right)=\underset{\mathrm{z}\rightarrow\mathrm{z}_{\mathrm{1}} } {\mathrm{lim}}\frac{\left(\mathrm{z}−\mathrm{z}_{\mathrm{1}} \right)}{\left(\mathrm{z}−\mathrm{z}_{\mathrm{1}} \right)\left(\mathrm{z}−\mathrm{z}_{\mathrm{2}} \right)}= \\ $$$$\frac{\mathrm{1}}{\mathrm{z}_{\mathrm{1}} −\mathrm{z}_{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2i}\sqrt{\mathrm{2}}}=\frac{−\mathrm{i}\sqrt{\mathrm{2}}}{\mathrm{4}}. \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{4}} +\mathrm{2x}^{\mathrm{2}} +\mathrm{3}}=\mathrm{2}\pi\mathrm{i}×\left(\frac{−\mathrm{i}\sqrt{\mathrm{2}}}{\mathrm{4}}\right)=\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$
