Menu Close

calculate-0-dx-x-4-x-2-3-2-

Tinku Tara 0 Comments
Pin




Question Number 88928 by mathmax by abdo last updated on 13/Apr/20
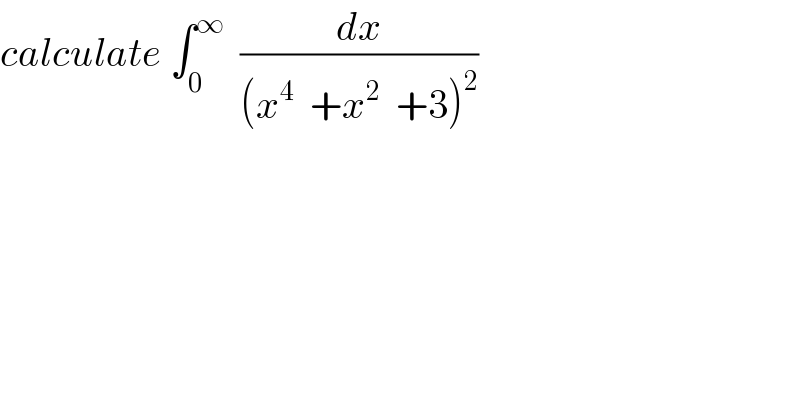
calculate ∫_0 ^∞ (dx/((x^4 +x^2 +3)^2 ))
$${calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{\left({x}^{\mathrm{4}} \:\:+{x}^{\mathrm{2}} \:\:+\mathrm{3}\right)^{\mathrm{2}} } \\ $$
Commented by mathmax by abdo last updated on 15/Apr/20
A =∫_0 ^∞ (dx/((x^4 +x^2 +3)^2 )) ⇒2A =∫_(−∞) ^(+∞) (dx/((x^4 +x^2 +3)^2 )) let ϕ(z)=(1/((z^4 +z^2 +3)^2 )) poles of ϕ? z^4 +z^2 +3 =0⇒t^2 +t+3=0 (t=z^2 ) Δ=1−12 =−11 ⇒t_1 =((−1+i(√(11)))/2) and t_2 =((−1−i(√(11)))/2) ∣t_1 ∣=(1/2)(√(1+11))=(1/2)(2(√3))=(√(3 )) ⇒t_1 =(√3)e^(−iarctan((√(11)))) t_2 =(√3)e^(iarctan((√(11)))) ⇒ϕ(z)=(1/((t−t_1 )^2 (t−t_2 )^2 )) =(1/((z^2 −(√3)e^(−iarctan((√(11)))) )^2 (z^2 −(√3)e^(iarctan((√(11)))) )^2 )) =(1/((z−αe^(−(i/2)arctan((√(11)))) )^2 (z+α e^(−(i/2)arctan((√(11)))) )^2 (z−α e^((i/2)arctan((√(11)))) )^2 (z+α e^((i/2)arctan((√(11)))) )^2 )) (with α =^4 (√3)) ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ { Res(ϕ,α e^((i/2)arctan((√(11)))) )+Res(ϕ,−α e^(−(i/2)arctan((√(11)))) } Res(ϕ,α e^((i/2)arctan((√(11)))) ) =lim_(z→αe^((i/2)arctan((√(11)))) ) (1/((2−1)!)){(z−αe^((i/2)arcan((√(11)))) )^2 ϕ(z)}^((1)) =lim_(z→α e^((i/2)arctan((√(11)))) ) {(1/((z+α e^(−(i/2)arctan((√(11)))) )^2 (z^2 −(√3)e^(iarctan((√(11)))) )^2 )) }^((1)) ....be continued...
$${A}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{\left({x}^{\mathrm{4}} \:+{x}^{\mathrm{2}} \:+\mathrm{3}\right)^{\mathrm{2}} }\:\Rightarrow\mathrm{2}{A}\:=\int_{−\infty} ^{+\infty} \:\frac{{dx}}{\left({x}^{\mathrm{4}} \:+{x}^{\mathrm{2}} \:+\mathrm{3}\right)^{\mathrm{2}} } \\ $$$${let}\:\varphi\left({z}\right)=\frac{\mathrm{1}}{\left({z}^{\mathrm{4}} \:+{z}^{\mathrm{2}} \:+\mathrm{3}\right)^{\mathrm{2}} }\:\:{poles}\:{of}\:\varphi? \\ $$$${z}^{\mathrm{4}} \:+{z}^{\mathrm{2}} \:+\mathrm{3}\:=\mathrm{0}\Rightarrow{t}^{\mathrm{2}} \:+{t}+\mathrm{3}=\mathrm{0}\:\:\left({t}={z}^{\mathrm{2}} \right) \\ $$$$\Delta=\mathrm{1}−\mathrm{12}\:=−\mathrm{11}\:\Rightarrow{t}_{\mathrm{1}} =\frac{−\mathrm{1}+{i}\sqrt{\mathrm{11}}}{\mathrm{2}}\:\:{and}\:{t}_{\mathrm{2}} =\frac{−\mathrm{1}−{i}\sqrt{\mathrm{11}}}{\mathrm{2}} \\ $$$$\mid{t}_{\mathrm{1}} \mid=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{1}+\mathrm{11}}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}\sqrt{\mathrm{3}}\right)=\sqrt{\mathrm{3}\:}\:\Rightarrow{t}_{\mathrm{1}} =\sqrt{\mathrm{3}}{e}^{−{iarctan}\left(\sqrt{\mathrm{11}}\right)} \\ $$$${t}_{\mathrm{2}} =\sqrt{\mathrm{3}}{e}^{{iarctan}\left(\sqrt{\mathrm{11}}\right)} \:\Rightarrow\varphi\left({z}\right)=\frac{\mathrm{1}}{\left({t}−{t}_{\mathrm{1}} \right)^{\mathrm{2}} \left({t}−{t}_{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\left({z}^{\mathrm{2}} −\sqrt{\mathrm{3}}{e}^{−{iarctan}\left(\sqrt{\mathrm{11}}\right)} \right)^{\mathrm{2}} \left({z}^{\mathrm{2}} −\sqrt{\mathrm{3}}{e}^{{iarctan}\left(\sqrt{\mathrm{11}}\right)} \right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\left({z}−\alpha{e}^{−\frac{{i}}{\mathrm{2}}{arctan}\left(\sqrt{\mathrm{11}}\right)} \right)^{\mathrm{2}} \left({z}+\alpha\:{e}^{−\frac{{i}}{\mathrm{2}}{arctan}\left(\sqrt{\mathrm{11}}\right)} \right)^{\mathrm{2}} \left({z}−\alpha\:{e}^{\frac{{i}}{\mathrm{2}}{arctan}\left(\sqrt{\mathrm{11}}\right)} \right)^{\mathrm{2}} \left({z}+\alpha\:{e}^{\frac{{i}}{\mathrm{2}}{arctan}\left(\sqrt{\mathrm{11}}\right)} \right)^{\mathrm{2}} } \\ $$$$\left({with}\:\alpha\:=^{\mathrm{4}} \sqrt{\mathrm{3}}\right) \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:\left\{\:{Res}\left(\varphi,\alpha\:{e}^{\frac{{i}}{\mathrm{2}}{arctan}\left(\sqrt{\mathrm{11}}\right)} \right)+{Res}\left(\varphi,−\alpha\:{e}^{−\frac{{i}}{\mathrm{2}}{arctan}\left(\sqrt{\mathrm{11}}\right)} \right\}\right. \\ $$$${Res}\left(\varphi,\alpha\:{e}^{\frac{{i}}{\mathrm{2}}{arctan}\left(\sqrt{\mathrm{11}}\right)} \right)\:={lim}_{{z}\rightarrow\alpha{e}^{\frac{{i}}{\mathrm{2}}{arctan}\left(\sqrt{\mathrm{11}}\right)} } \:\:\frac{\mathrm{1}}{\left(\mathrm{2}−\mathrm{1}\right)!}\left\{\left({z}−\alpha{e}^{\frac{{i}}{\mathrm{2}}{arcan}\left(\sqrt{\mathrm{11}}\right)} \right)^{\mathrm{2}} \varphi\left({z}\right)\right\}^{\left(\mathrm{1}\right)} \\ $$$$={lim}_{{z}\rightarrow\alpha\:{e}^{\frac{{i}}{\mathrm{2}}{arctan}\left(\sqrt{\mathrm{11}}\right)} } \:\:\:\:\left\{\frac{\mathrm{1}}{\left({z}+\alpha\:{e}^{−\frac{{i}}{\mathrm{2}}{arctan}\left(\sqrt{\mathrm{11}}\right)} \right)^{\mathrm{2}} \left({z}^{\mathrm{2}} −\sqrt{\mathrm{3}}{e}^{{iarctan}\left(\sqrt{\mathrm{11}}\right)} \right)^{\mathrm{2}} }\:\:\right\}^{\left(\mathrm{1}\right)} \\ $$$$….{be}\:{continued}… \\ $$
Commented by mathmax by abdo last updated on 15/Apr/20
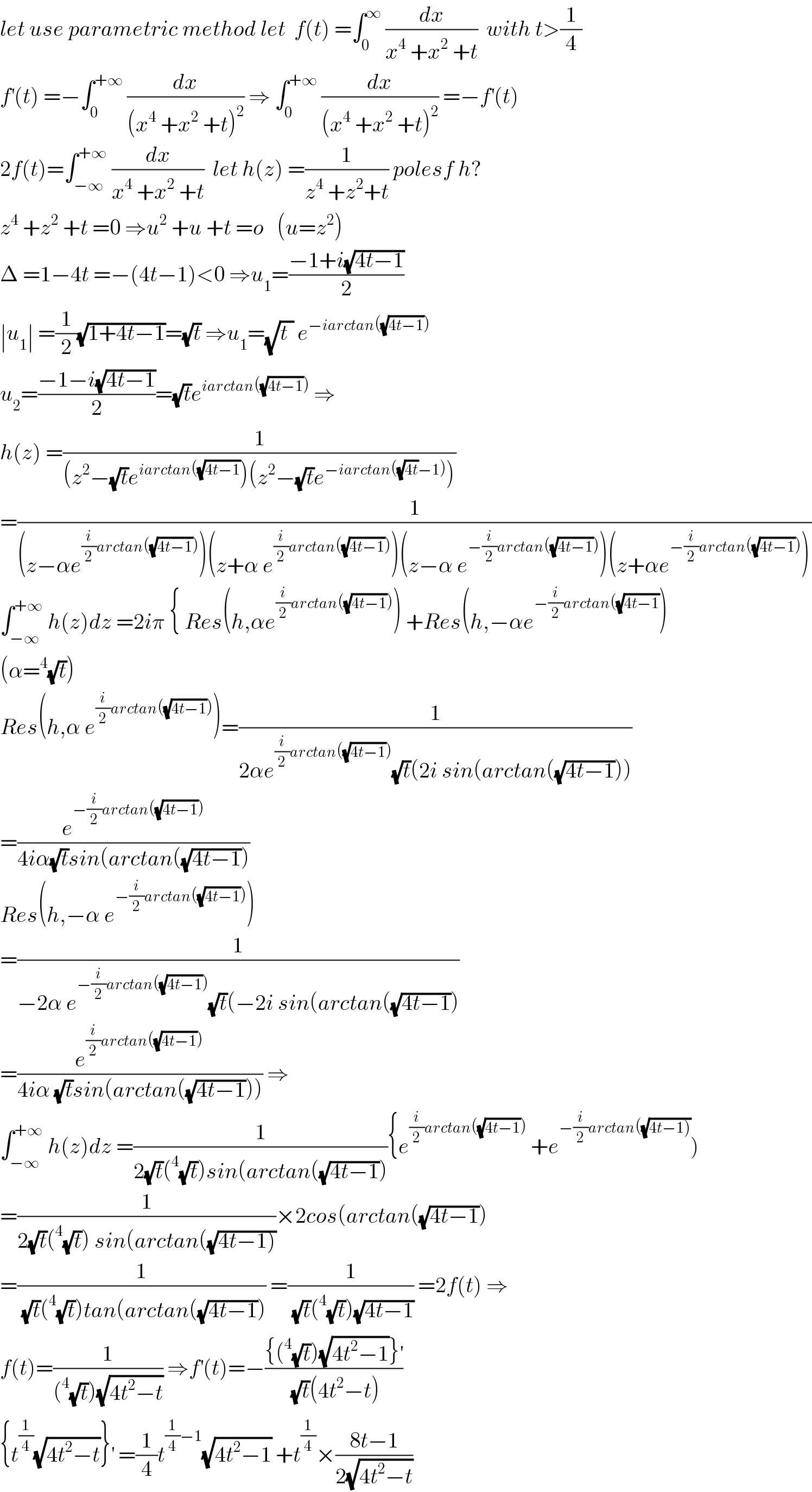
let use parametric method let f(t) =∫_0 ^∞ (dx/(x^4 +x^2 +t)) with t>(1/4) f^′ (t) =−∫_0 ^(+∞) (dx/((x^4 +x^2 +t)^2 )) ⇒ ∫_0 ^(+∞) (dx/((x^4 +x^2 +t)^2 )) =−f^′ (t) 2f(t)=∫_(−∞) ^(+∞) (dx/(x^4 +x^2 +t)) let h(z) =(1/(z^4 +z^2 +t)) polesf h? z^4 +z^2 +t =0 ⇒u^2 +u +t =o (u=z^2 ) Δ =1−4t =−(4t−1)<0 ⇒u_1 =((−1+i(√(4t−1)))/2) ∣u_1 ∣ =(1/2)(√(1+4t−1))=(√t) ⇒u_1 =(√t_ ) e^(−iarctan((√(4t−1)))) u_2 =((−1−i(√(4t−1)))/2)=(√t)e^(iarctan((√(4t−1)))) ⇒ h(z) =(1/((z^2 −(√t)e^(iarctan((√(4t−1))) )(z^2 −(√t)e^(−iarctan((√(4t))−1)) ))) =(1/((z−αe^((i/2)arctan((√(4t−1)))) )(z+α e^((i/2)arctan((√(4t−1)))) )(z−α e^(−(i/2)arctan((√(4t−1)))) )(z+αe^(−(i/2)arctan((√(4t−1)))) ))) ∫_(−∞) ^(+∞) h(z)dz =2iπ { Res(h,αe^((i/2)arctan((√(4t−1)))) ) +Res(h,−αe^(−(i/2)arctan((√(4t−1))) ) (α=^4 (√t)) Res(h,α e^((i/2)arctan((√(4t−1)))) )=(1/(2αe^((i/2)arctan((√(4t−1)))) (√t)(2i sin(arctan((√(4t−1)))))) =(e^(−(i/2)arctan((√(4t−1)))) /(4iα(√t)sin(arctan((√(4t−1))))) Res(h,−α e^(−(i/2)arctan((√(4t−1)))) ) =(1/(−2α e^(−(i/2)arctan((√(4t−1)))) (√t)(−2i sin(arctan((√(4t−1))))) =(e^((i/2)arctan((√(4t−1)))) /(4iα (√t)sin(arctan((√(4t−1)))))) ⇒ ∫_(−∞) ^(+∞) h(z)dz =(1/(2(√t)(^4 (√t))sin(arctan((√(4t−1))))){e^((i/2)arctan((√(4t−1)))) +e^(−(i/2)arctan((√(4t−1)))) ) =(1/(2(√t)(^4 (√t)) sin(arctan((√(4t−1)))))×2cos(arctan((√(4t−1))) =(1/( (√t)(^4 (√t))tan(arctan((√(4t−1))))) =(1/( (√t)(^4 (√t))(√(4t−1)))) =2f(t) ⇒ f(t)=(1/((^4 (√t))(√(4t^2 −t)))) ⇒f^′ (t)=−(({(^4 (√t))(√(4t^2 −1))}^′ )/( (√t)(4t^2 −t))) {t^(1/4) (√(4t^2 −t))}^′ =(1/4)t^((1/4)−1) (√(4t^2 −1)) +t^(1/4) ×((8t−1)/(2(√(4t^2 −t))))
$${let}\:{use}\:{parametric}\:{method}\:{let}\:\:{f}\left({t}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\frac{{dx}}{{x}^{\mathrm{4}} \:+{x}^{\mathrm{2}} \:+{t}}\:\:{with}\:{t}>\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${f}^{'} \left({t}\right)\:=−\int_{\mathrm{0}} ^{+\infty} \:\frac{{dx}}{\left({x}^{\mathrm{4}} \:+{x}^{\mathrm{2}} \:+{t}\right)^{\mathrm{2}} }\:\Rightarrow\:\int_{\mathrm{0}} ^{+\infty} \:\frac{{dx}}{\left({x}^{\mathrm{4}} \:+{x}^{\mathrm{2}} \:+{t}\right)^{\mathrm{2}} }\:=−{f}^{'} \left({t}\right) \\ $$$$\mathrm{2}{f}\left({t}\right)=\int_{−\infty} ^{+\infty} \:\frac{{dx}}{{x}^{\mathrm{4}} \:+{x}^{\mathrm{2}} \:+{t}}\:\:{let}\:{h}\left({z}\right)\:=\frac{\mathrm{1}}{{z}^{\mathrm{4}} \:+{z}^{\mathrm{2}} +{t}}\:{polesf}\:{h}? \\ $$$${z}^{\mathrm{4}} \:+{z}^{\mathrm{2}} \:+{t}\:=\mathrm{0}\:\Rightarrow{u}^{\mathrm{2}} \:+{u}\:+{t}\:={o}\:\:\:\left({u}={z}^{\mathrm{2}} \right) \\ $$$$\Delta\:=\mathrm{1}−\mathrm{4}{t}\:=−\left(\mathrm{4}{t}−\mathrm{1}\right)<\mathrm{0}\:\Rightarrow{u}_{\mathrm{1}} =\frac{−\mathrm{1}+{i}\sqrt{\mathrm{4}{t}−\mathrm{1}}}{\mathrm{2}} \\ $$$$\mid{u}_{\mathrm{1}} \mid\:=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{1}+\mathrm{4}{t}−\mathrm{1}}=\sqrt{{t}}\:\Rightarrow{u}_{\mathrm{1}} =\sqrt{{t}_{} }\:{e}^{−{iarctan}\left(\sqrt{\mathrm{4}{t}−\mathrm{1}}\right)} \\ $$$${u}_{\mathrm{2}} =\frac{−\mathrm{1}−{i}\sqrt{\mathrm{4}{t}−\mathrm{1}}}{\mathrm{2}}=\sqrt{{t}}{e}^{{iarctan}\left(\sqrt{\mathrm{4}{t}−\mathrm{1}}\right)} \:\Rightarrow \\ $$$${h}\left({z}\right)\:=\frac{\mathrm{1}}{\left({z}^{\mathrm{2}} −\sqrt{{t}}{e}^{{iarctan}\left(\sqrt{\mathrm{4}{t}−\mathrm{1}}\right.} \right)\left({z}^{\mathrm{2}} −\sqrt{{t}}{e}^{−{iarctan}\left(\sqrt{\mathrm{4}{t}}−\mathrm{1}\right)} \right)} \\ $$$$=\frac{\mathrm{1}}{\left({z}−\alpha{e}^{\frac{{i}}{\mathrm{2}}{arctan}\left(\sqrt{\mathrm{4}{t}−\mathrm{1}}\right)} \right)\left({z}+\alpha\:{e}^{\frac{{i}}{\mathrm{2}}{arctan}\left(\sqrt{\mathrm{4}{t}−\mathrm{1}}\right)} \right)\left({z}−\alpha\:{e}^{−\frac{{i}}{\mathrm{2}}{arctan}\left(\sqrt{\mathrm{4}{t}−\mathrm{1}}\right)} \right)\left({z}+\alpha{e}^{−\frac{{i}}{\mathrm{2}}{arctan}\left(\sqrt{\mathrm{4}{t}−\mathrm{1}}\right)} \right)} \\ $$$$\int_{−\infty} ^{+\infty} \:{h}\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:\left\{\:{Res}\left({h},\alpha{e}^{\frac{{i}}{\mathrm{2}}{arctan}\left(\sqrt{\mathrm{4}{t}−\mathrm{1}}\right)} \right)\:+{Res}\left({h},−\alpha{e}^{−\frac{{i}}{\mathrm{2}}{arctan}\left(\sqrt{\mathrm{4}{t}−\mathrm{1}}\right.} \right)\right. \\ $$$$\left(\alpha=^{\mathrm{4}} \sqrt{{t}}\right) \\ $$$${Res}\left({h},\alpha\:{e}^{\frac{{i}}{\mathrm{2}}{arctan}\left(\sqrt{\mathrm{4}{t}−\mathrm{1}}\right)} \right)=\frac{\mathrm{1}}{\mathrm{2}\alpha{e}^{\frac{{i}}{\mathrm{2}}{arctan}\left(\sqrt{\mathrm{4}{t}−\mathrm{1}}\right)} \sqrt{{t}}\left(\mathrm{2}{i}\:{sin}\left({arctan}\left(\sqrt{\mathrm{4}{t}−\mathrm{1}}\right)\right)\right.} \\ $$$$=\frac{{e}^{−\frac{{i}}{\mathrm{2}}{arctan}\left(\sqrt{\mathrm{4}{t}−\mathrm{1}}\right)} }{\mathrm{4}{i}\alpha\sqrt{{t}}{sin}\left({arctan}\left(\sqrt{\mathrm{4}{t}−\mathrm{1}}\right)\right.} \\ $$$${Res}\left({h},−\alpha\:{e}^{−\frac{{i}}{\mathrm{2}}{arctan}\left(\sqrt{\mathrm{4}{t}−\mathrm{1}}\right)} \right) \\ $$$$=\frac{\mathrm{1}}{−\mathrm{2}\alpha\:{e}^{−\frac{{i}}{\mathrm{2}}{arctan}\left(\sqrt{\mathrm{4}{t}−\mathrm{1}}\right)} \sqrt{{t}}\left(−\mathrm{2}{i}\:{sin}\left({arctan}\left(\sqrt{\mathrm{4}{t}−\mathrm{1}}\right)\right.\right.} \\ $$$$=\frac{{e}^{\frac{{i}}{\mathrm{2}}{arctan}\left(\sqrt{\mathrm{4}{t}−\mathrm{1}}\right)} }{\mathrm{4}{i}\alpha\:\sqrt{{t}}{sin}\left({arctan}\left(\sqrt{\mathrm{4}{t}−\mathrm{1}}\right)\right)}\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:{h}\left({z}\right){dz}\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{{t}}\left(^{\mathrm{4}} \sqrt{{t}}\right){sin}\left({arctan}\left(\sqrt{\mathrm{4}{t}−\mathrm{1}}\right)\right.}\left\{{e}^{\frac{{i}}{\mathrm{2}}{arctan}\left(\sqrt{\mathrm{4}{t}−\mathrm{1}}\right)} \:+{e}^{−\frac{{i}}{\mathrm{2}}{arctan}\left(\sqrt{\left.\mathrm{4}{t}−\mathrm{1}\right)}\right.} \right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{{t}}\left(^{\mathrm{4}} \sqrt{{t}}\right)\:{sin}\left({arctan}\left(\sqrt{\left.\mathrm{4}{t}−\mathrm{1}\right)}\right.\right.}×\mathrm{2}{cos}\left({arctan}\left(\sqrt{\mathrm{4}{t}−\mathrm{1}}\right)\right. \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{{t}}\left(^{\mathrm{4}} \sqrt{{t}}\right){tan}\left({arctan}\left(\sqrt{\mathrm{4}{t}−\mathrm{1}}\right)\right.}\:=\frac{\mathrm{1}}{\:\sqrt{{t}}\left(^{\mathrm{4}} \sqrt{{t}}\right)\sqrt{\mathrm{4}{t}−\mathrm{1}}}\:=\mathrm{2}{f}\left({t}\right)\:\Rightarrow \\ $$$${f}\left({t}\right)=\frac{\mathrm{1}}{\left(^{\mathrm{4}} \sqrt{{t}}\right)\sqrt{\mathrm{4}{t}^{\mathrm{2}} −{t}}}\:\Rightarrow{f}^{'} \left({t}\right)=−\frac{\left\{\left(^{\mathrm{4}} \sqrt{{t}}\right)\sqrt{\mathrm{4}{t}^{\mathrm{2}} −\mathrm{1}}\right\}^{'} }{\:\sqrt{{t}}\left(\mathrm{4}{t}^{\mathrm{2}} −{t}\right)} \\ $$$$\left\{{t}^{\frac{\mathrm{1}}{\mathrm{4}}} \sqrt{\mathrm{4}{t}^{\mathrm{2}} −{t}}\right\}^{'} \:=\frac{\mathrm{1}}{\mathrm{4}}{t}^{\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{1}} \sqrt{\mathrm{4}{t}^{\mathrm{2}} −\mathrm{1}}\:+{t}^{\frac{\mathrm{1}}{\mathrm{4}}} ×\frac{\mathrm{8}{t}−\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{4}{t}^{\mathrm{2}} −{t}}} \\ $$
Commented by mathmax by abdo last updated on 15/Apr/20
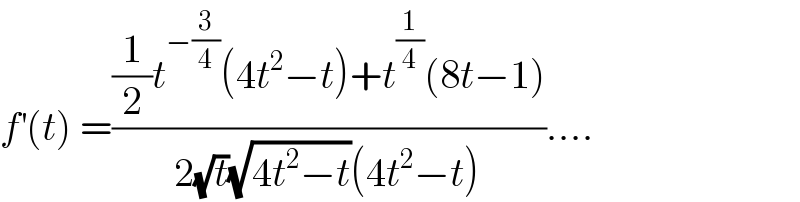
f^′ (t) =(((1/2)t^(−(3/4)) (4t^2 −t)+t^(1/4) (8t−1))/(2(√t)(√(4t^2 −t))(4t^2 −t)))....
$${f}^{'} \left({t}\right)\:=\frac{\frac{\mathrm{1}}{\mathrm{2}}{t}^{−\frac{\mathrm{3}}{\mathrm{4}}} \left(\mathrm{4}{t}^{\mathrm{2}} −{t}\right)+{t}^{\frac{\mathrm{1}}{\mathrm{4}}} \left(\mathrm{8}{t}−\mathrm{1}\right)}{\mathrm{2}\sqrt{{t}}\sqrt{\mathrm{4}{t}^{\mathrm{2}} −{t}}\left(\mathrm{4}{t}^{\mathrm{2}} −{t}\right)}…. \\ $$
Commented by mathmax by abdo last updated on 15/Apr/20
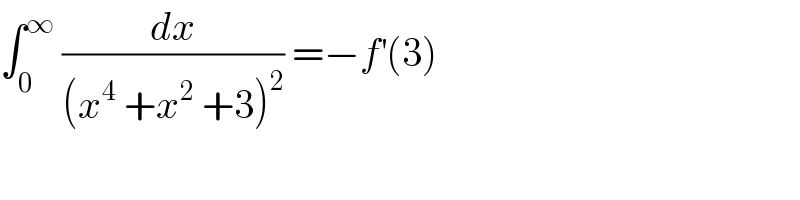
∫_0 ^∞ (dx/((x^4 +x^2 +3)^2 )) =−f^′ (3)
$$\int_{\mathrm{0}} ^{\infty} \:\frac{{dx}}{\left({x}^{\mathrm{4}} \:+{x}^{\mathrm{2}} \:+\mathrm{3}\right)^{\mathrm{2}} }\:=−{f}^{'} \left(\mathrm{3}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *