Question Number 145044 by mathmax by abdo last updated on 01/Jul/21
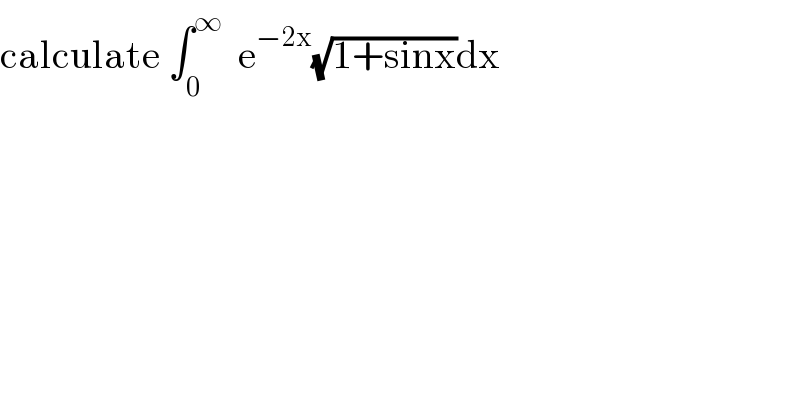
$$\mathrm{calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\mathrm{e}^{−\mathrm{2x}} \sqrt{\mathrm{1}+\mathrm{sinx}}\mathrm{dx} \\ $$
Answered by qaz last updated on 02/Jul/21
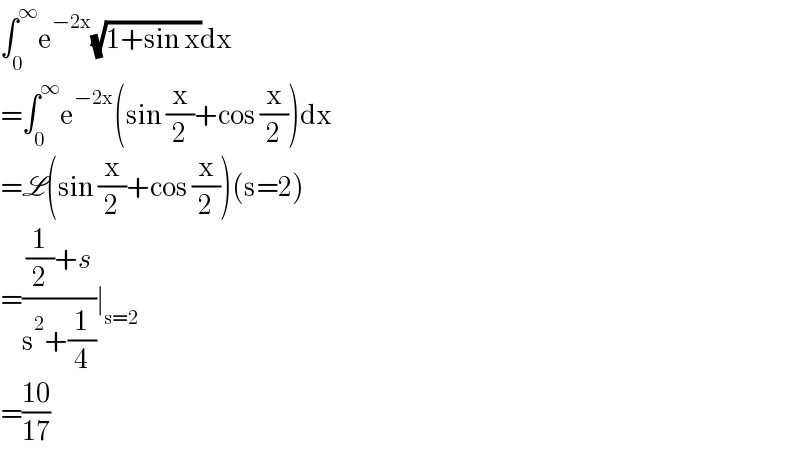
$$\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{2x}} \sqrt{\mathrm{1}+\mathrm{sin}\:\mathrm{x}}\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{2x}} \left(\mathrm{sin}\:\frac{\mathrm{x}}{\mathrm{2}}+\mathrm{cos}\:\frac{\mathrm{x}}{\mathrm{2}}\right)\mathrm{dx} \\ $$$$=\mathscr{L}\left(\mathrm{sin}\:\frac{\mathrm{x}}{\mathrm{2}}+\mathrm{cos}\:\frac{\mathrm{x}}{\mathrm{2}}\right)\left(\mathrm{s}=\mathrm{2}\right) \\ $$$$=\frac{\frac{\mathrm{1}}{\mathrm{2}}+{s}}{\mathrm{s}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}}}\mid_{\mathrm{s}=\mathrm{2}} \\ $$$$=\frac{\mathrm{10}}{\mathrm{17}} \\ $$
Commented by mathmax by abdo last updated on 03/Jul/21

$$\mathrm{answer}\:\mathrm{not}\:\mathrm{correct}\:\mathrm{sir}\:\mathrm{gaz} \\ $$
Answered by mnjuly1970 last updated on 02/Jul/21

$$\sqrt{\mathrm{1}+{sin}\left({x}\right)}\:=\:\mid\:{sin}\left(\frac{{x}}{\mathrm{2}}\right)+{cos}\left(\frac{{x}}{\mathrm{2}}\right)\mid \\ $$
Answered by mathmax by abdo last updated on 02/Jul/21
![I=∫_0 ^∞ e^(−2x) (√(1+sinx))dx we have 1+sinx=(cos((x/2))+sin((x/2)))^2 ⇒ (√(1+sinx))=∣cos((x/2))+sin((x/2))∣ ⇒ I=∫_0 ^∞ e^(−2x) ∣cos((x/2))+sin((x/2))∣dx=_((x/2)=t) 2 ∫_0 ^∞ e^(−4t) ∣cost+sint∣dt =2∫_0 ^∞ e^(−4t) ∣(√2)sin(t+(π/4))∣dt=2(√2)∫_0 ^∞ e^(−4t) ∣sin(t+(π/4))∣dt =_(t+(π/4)=y) 2(√2)∫_(π/4) ^(+∞) e^(−4(y−(π/4))) ∣siny∣dy =2(√2)e^π ∫_(π/4) ^(+∞) e^(−4y) ∣siny∣dy =2(√2)e^π (∫_0 ^∞ e^(−4y) ∣siny∣dy−∫_0 ^(π/4) e^(−4y) siny dy) we have ∫_0 ^(π/4) e^(−4y) siny dy =Im(∫_0 ^(π/4) e^(−4y+iy) dy) ∫_0 ^(π/4) e^((−4+i)y) dy =[(1/(−4+i))e^((−4+i)y) ]_0 ^(π/4) =−(1/(4−i))(e^((−4+i)(π/4)) −1) =−((4+i)/(17))(e^(−π) ((1/( (√2)))+(i/( (√2))))−1) =−(1/(17))(4+i)((e^(−π) /( (√2))) +i (e^(−π) /( (√2)))−1) =−(1/(17))(((4e^(−π) )/( (√2)))+4i(e^(−π) /( (√2)))−4+i(e^(−π) /( (√2)))−(e^(−π) /( (√2)))−i) ⇒ ∫_0 ^(π/4) e^(−4y) sinydy=−(1/(17))(((4e^(−π) )/( (√2))) +(e^(−π) /( (√2)))−1)=(1/(17))(1−((5e^(−π) )/( (√2)))) ∫_0 ^∞ e^(−4y) ∣siny∣dy =Σ_(n=0) ^∞ ∫_(nπ) ^((n+1)π) e^(−4y) ∣siny∣dy =_(y=nπ+z) Σ_(n=0) ^∞ ∫_0 ^π e^(−4(nπ+z)) sinz dz (sinz≥0 on [0,π]) =Σ_(n=0) ^∞ e^(−4nπ) ∫_0 ^π e^(−4z) sinzdz we have ∫_0 ^π e^(−4z) sinz dz =Im(∫_0 ^π e^(−4z+iz) dz) ∫_0 ^π e^((−4+i)z) dz =[(1/(−4+i))e^((−4+i)z) ]_0 ^π =−(1/(4−i))(e^((−4+i)π) −1) =−((4+i)/(17))(−e^(−4π) −1) =((4+i)/(17))(1+e^(−4π) ) ⇒ ∫_0 ^π e^(−4z) sinz dz =((1+e^(−4π) )/(17)) ⇒ ∫_0 ^∞ e^(−4y) ∣siny∣dy =((1+e^(−4π) )/(17))Σ_(n=0) ^∞ (e^(−4π) )^n =((1+e^(−4π) )/(17))×(1/(1−e^(−4π) )) =((1+e^(4π) )/(17(1−e^(−4π) ))) ⇒ I =2(√2)e^π (((1+e^(4π) )/(17(1−e^(4π) )))−(1/(17))(1−((5e^(−π) )/( (√2)))) =((2(√2))/(17))(((1+e^(4π) )/(1−e^(4π) ))−1+((5e^(−π) )/( (√2))))](https://www.tinkutara.com/question/Q145117.png)
$$\mathrm{I}=\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{2x}} \sqrt{\mathrm{1}+\mathrm{sinx}}\mathrm{dx}\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{1}+\mathrm{sinx}=\left(\mathrm{cos}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)+\mathrm{sin}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\right)^{\mathrm{2}} \:\Rightarrow \\ $$$$\sqrt{\mathrm{1}+\mathrm{sinx}}=\mid\mathrm{cos}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)+\mathrm{sin}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\mid\:\Rightarrow \\ $$$$\mathrm{I}=\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{2x}} \mid\mathrm{cos}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)+\mathrm{sin}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\mid\mathrm{dx}=_{\frac{\mathrm{x}}{\mathrm{2}}=\mathrm{t}} \:\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{4t}} \mid\mathrm{cost}+\mathrm{sint}\mid\mathrm{dt} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{4t}} \mid\sqrt{\mathrm{2}}\mathrm{sin}\left(\mathrm{t}+\frac{\pi}{\mathrm{4}}\right)\mid\mathrm{dt}=\mathrm{2}\sqrt{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{4t}} \mid\mathrm{sin}\left(\mathrm{t}+\frac{\pi}{\mathrm{4}}\right)\mid\mathrm{dt} \\ $$$$=_{\mathrm{t}+\frac{\pi}{\mathrm{4}}=\mathrm{y}} \:\:\mathrm{2}\sqrt{\mathrm{2}}\int_{\frac{\pi}{\mathrm{4}}} ^{+\infty} \:\mathrm{e}^{−\mathrm{4}\left(\mathrm{y}−\frac{\pi}{\mathrm{4}}\right)} \mid\mathrm{siny}\mid\mathrm{dy} \\ $$$$=\mathrm{2}\sqrt{\mathrm{2}}\mathrm{e}^{\pi} \:\int_{\frac{\pi}{\mathrm{4}}} ^{+\infty} \:\mathrm{e}^{−\mathrm{4y}} \mid\mathrm{siny}\mid\mathrm{dy} \\ $$$$=\mathrm{2}\sqrt{\mathrm{2}}\mathrm{e}^{\pi} \left(\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{4y}} \mid\mathrm{siny}\mid\mathrm{dy}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\mathrm{e}^{−\mathrm{4y}} \:\mathrm{siny}\:\mathrm{dy}\right)\:\mathrm{we}\:\mathrm{have} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\mathrm{e}^{−\mathrm{4y}} \mathrm{siny}\:\mathrm{dy}\:=\mathrm{Im}\left(\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\mathrm{e}^{−\mathrm{4y}+\mathrm{iy}} \:\mathrm{dy}\right) \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\mathrm{e}^{\left(−\mathrm{4}+\mathrm{i}\right)\mathrm{y}} \:\mathrm{dy}\:=\left[\frac{\mathrm{1}}{−\mathrm{4}+\mathrm{i}}\mathrm{e}^{\left(−\mathrm{4}+\mathrm{i}\right)\mathrm{y}} \right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{4}−\mathrm{i}}\left(\mathrm{e}^{\left(−\mathrm{4}+\mathrm{i}\right)\frac{\pi}{\mathrm{4}}} −\mathrm{1}\right) \\ $$$$=−\frac{\mathrm{4}+\mathrm{i}}{\mathrm{17}}\left(\mathrm{e}^{−\pi} \left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}+\frac{\mathrm{i}}{\:\sqrt{\mathrm{2}}}\right)−\mathrm{1}\right) \\ $$$$=−\frac{\mathrm{1}}{\mathrm{17}}\left(\mathrm{4}+\mathrm{i}\right)\left(\frac{\mathrm{e}^{−\pi} }{\:\sqrt{\mathrm{2}}}\:+\mathrm{i}\:\frac{\mathrm{e}^{−\pi} }{\:\sqrt{\mathrm{2}}}−\mathrm{1}\right) \\ $$$$=−\frac{\mathrm{1}}{\mathrm{17}}\left(\frac{\mathrm{4e}^{−\pi} }{\:\sqrt{\mathrm{2}}}+\mathrm{4i}\frac{\mathrm{e}^{−\pi} }{\:\sqrt{\mathrm{2}}}−\mathrm{4}+\mathrm{i}\frac{\mathrm{e}^{−\pi} }{\:\sqrt{\mathrm{2}}}−\frac{\mathrm{e}^{−\pi} }{\:\sqrt{\mathrm{2}}}−\mathrm{i}\right)\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\mathrm{e}^{−\mathrm{4y}} \:\mathrm{sinydy}=−\frac{\mathrm{1}}{\mathrm{17}}\left(\frac{\mathrm{4e}^{−\pi} }{\:\sqrt{\mathrm{2}}}\:+\frac{\mathrm{e}^{−\pi} }{\:\sqrt{\mathrm{2}}}−\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{17}}\left(\mathrm{1}−\frac{\mathrm{5e}^{−\pi} }{\:\sqrt{\mathrm{2}}}\right) \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{4y}} \mid\mathrm{siny}\mid\mathrm{dy}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\int_{\mathrm{n}\pi} ^{\left(\mathrm{n}+\mathrm{1}\right)\pi} \:\mathrm{e}^{−\mathrm{4y}} \mid\mathrm{siny}\mid\mathrm{dy} \\ $$$$=_{\mathrm{y}=\mathrm{n}\pi+\mathrm{z}} \:\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\int_{\mathrm{0}} ^{\pi} \:\mathrm{e}^{−\mathrm{4}\left(\mathrm{n}\pi+\mathrm{z}\right)} \mathrm{sinz}\:\mathrm{dz}\:\:\:\:\:\left(\mathrm{sinz}\geqslant\mathrm{0}\:\mathrm{on}\:\left[\mathrm{0},\pi\right]\right) \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{4n}\pi} \:\int_{\mathrm{0}} ^{\pi} \:\mathrm{e}^{−\mathrm{4z}} \mathrm{sinzdz}\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\int_{\mathrm{0}} ^{\pi} \:\mathrm{e}^{−\mathrm{4z}} \:\mathrm{sinz}\:\mathrm{dz}\:=\mathrm{Im}\left(\int_{\mathrm{0}} ^{\pi} \:\mathrm{e}^{−\mathrm{4z}+\mathrm{iz}} \mathrm{dz}\right) \\ $$$$\int_{\mathrm{0}} ^{\pi} \:\mathrm{e}^{\left(−\mathrm{4}+\mathrm{i}\right)\mathrm{z}} \mathrm{dz}\:=\left[\frac{\mathrm{1}}{−\mathrm{4}+\mathrm{i}}\mathrm{e}^{\left(−\mathrm{4}+\mathrm{i}\right)\mathrm{z}} \right]_{\mathrm{0}} ^{\pi} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{4}−\mathrm{i}}\left(\mathrm{e}^{\left(−\mathrm{4}+\mathrm{i}\right)\pi} −\mathrm{1}\right) \\ $$$$=−\frac{\mathrm{4}+\mathrm{i}}{\mathrm{17}}\left(−\mathrm{e}^{−\mathrm{4}\pi} −\mathrm{1}\right)\:=\frac{\mathrm{4}+\mathrm{i}}{\mathrm{17}}\left(\mathrm{1}+\mathrm{e}^{−\mathrm{4}\pi} \right)\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\pi} \:\mathrm{e}^{−\mathrm{4z}} \:\mathrm{sinz}\:\mathrm{dz}\:=\frac{\mathrm{1}+\mathrm{e}^{−\mathrm{4}\pi} }{\mathrm{17}}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\mathrm{e}^{−\mathrm{4y}} \mid\mathrm{siny}\mid\mathrm{dy}\:=\frac{\mathrm{1}+\mathrm{e}^{−\mathrm{4}\pi} }{\mathrm{17}}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(\mathrm{e}^{−\mathrm{4}\pi} \right)^{\mathrm{n}} \\ $$$$=\frac{\mathrm{1}+\mathrm{e}^{−\mathrm{4}\pi} }{\mathrm{17}}×\frac{\mathrm{1}}{\mathrm{1}−\mathrm{e}^{−\mathrm{4}\pi} }\:=\frac{\mathrm{1}+\mathrm{e}^{\mathrm{4}\pi} }{\mathrm{17}\left(\mathrm{1}−\mathrm{e}^{−\mathrm{4}\pi} \right)}\:\Rightarrow \\ $$$$\mathrm{I}\:=\mathrm{2}\sqrt{\mathrm{2}}\mathrm{e}^{\pi} \left(\frac{\mathrm{1}+\mathrm{e}^{\mathrm{4}\pi} }{\mathrm{17}\left(\mathrm{1}−\mathrm{e}^{\mathrm{4}\pi} \right)}−\frac{\mathrm{1}}{\mathrm{17}}\left(\mathrm{1}−\frac{\mathrm{5e}^{−\pi} }{\:\sqrt{\mathrm{2}}}\right)\right. \\ $$$$=\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{17}}\left(\frac{\mathrm{1}+\mathrm{e}^{\mathrm{4}\pi} }{\mathrm{1}−\mathrm{e}^{\mathrm{4}\pi} }−\mathrm{1}+\frac{\mathrm{5e}^{−\pi} }{\:\sqrt{\mathrm{2}}}\right) \\ $$
Commented by mathmax by abdo last updated on 02/Jul/21

$$\mathrm{I}=\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{17}}\left(\frac{\mathrm{1}+\mathrm{e}^{\mathrm{4}\pi} }{\mathrm{1}−\mathrm{e}^{−\mathrm{4}\pi} }−\mathrm{1}\:+\frac{\mathrm{5e}^{−\pi} }{\:\sqrt{\mathrm{2}}}\right) \\ $$
Commented by mnjuly1970 last updated on 03/Jul/21
$${very}\:{nice}\:{sir}\:{max}\:… \\ $$
Commented by qaz last updated on 04/Jul/21

$$\mathrm{nice}\:\mathrm{solution}\:\mathrm{sir} \\ $$
