Question Number 31093 by abdo imad last updated on 02/Mar/18
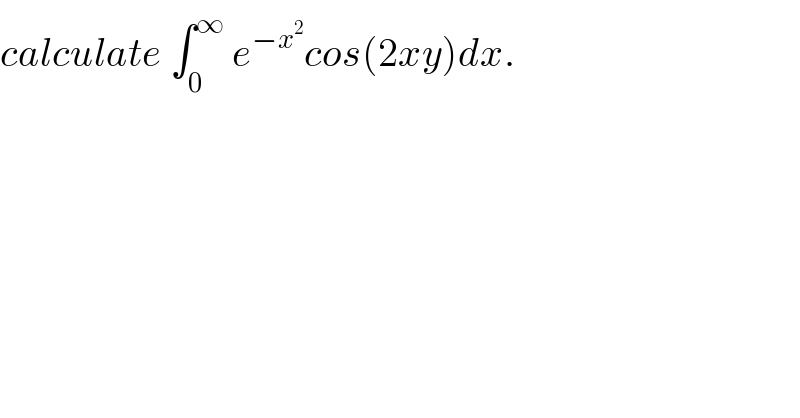
$${calculate}\:\int_{\mathrm{0}} ^{\infty} \:{e}^{−{x}^{\mathrm{2}} } {cos}\left(\mathrm{2}{xy}\right){dx}. \\ $$
Commented by abdo imad last updated on 04/Mar/18
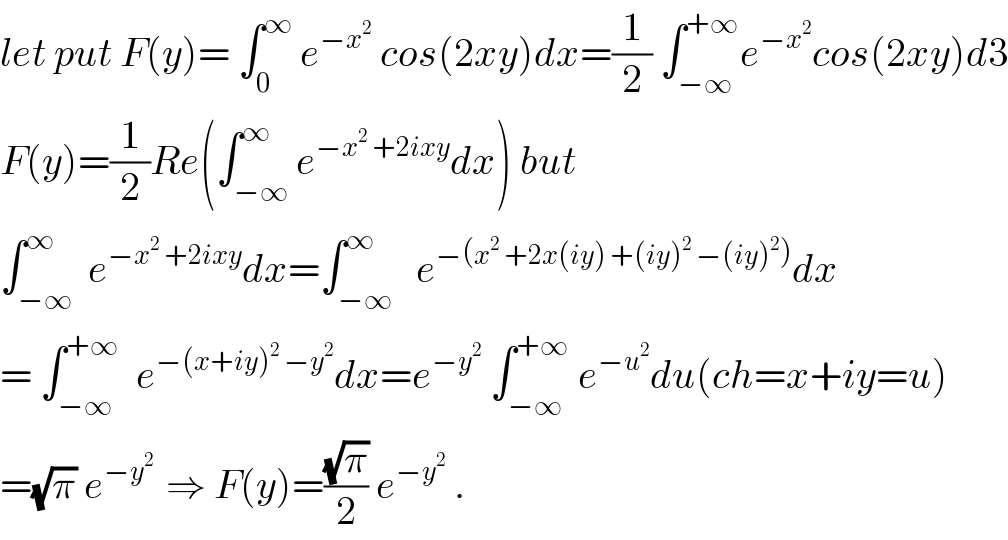
$${let}\:{put}\:{F}\left({y}\right)=\:\int_{\mathrm{0}} ^{\infty} \:{e}^{−{x}^{\mathrm{2}} } \:{cos}\left(\mathrm{2}{xy}\right){dx}=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{−\infty} ^{+\infty} {e}^{−{x}^{\mathrm{2}} } {cos}\left(\mathrm{2}{xy}\right){d}\mathrm{3} \\ $$$${F}\left({y}\right)=\frac{\mathrm{1}}{\mathrm{2}}{Re}\left(\int_{−\infty} ^{\infty} {e}^{−{x}^{\mathrm{2}} \:+\mathrm{2}{ixy}} {dx}\right)\:{but} \\ $$$$\int_{−\infty} ^{\infty} \:{e}^{−{x}^{\mathrm{2}} \:+\mathrm{2}{ixy}} {dx}=\int_{−\infty} ^{\infty} \:\:{e}^{−\left({x}^{\mathrm{2}} \:+\mathrm{2}{x}\left({iy}\right)\:+\left({iy}\right)^{\mathrm{2}} \:−\left({iy}\right)^{\mathrm{2}} \right)} {dx} \\ $$$$=\:\int_{−\infty} ^{+\infty} \:\:{e}^{−\left({x}+{iy}\right)^{\mathrm{2}} \:−{y}^{\mathrm{2}} } {dx}={e}^{−{y}^{\mathrm{2}} } \:\int_{−\infty} ^{+\infty} \:{e}^{−{u}^{\mathrm{2}} } {du}\left({ch}={x}+{iy}={u}\right) \\ $$$$=\sqrt{\pi}\:{e}^{−{y}^{\mathrm{2}} \:} \:\Rightarrow\:{F}\left({y}\right)=\frac{\sqrt{\pi}}{\mathrm{2}}\:{e}^{−{y}^{\mathrm{2}} } \:. \\ $$
