Question Number 99234 by abdomathmax last updated on 19/Jun/20
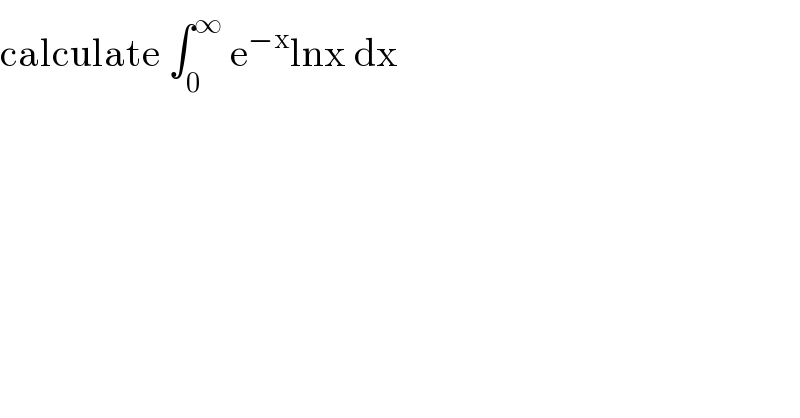
$$\mathrm{calculate}\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{x}} \mathrm{lnx}\:\mathrm{dx} \\ $$
Answered by maths mind last updated on 19/Jun/20
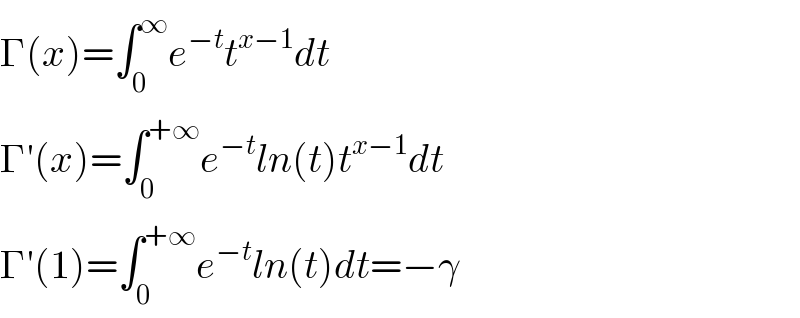
$$\Gamma\left({x}\right)=\int_{\mathrm{0}} ^{\infty} {e}^{−{t}} {t}^{{x}−\mathrm{1}} {dt} \\ $$$$\Gamma'\left({x}\right)=\int_{\mathrm{0}} ^{+\infty} {e}^{−{t}} {ln}\left({t}\right){t}^{{x}−\mathrm{1}} {dt} \\ $$$$\Gamma'\left(\mathrm{1}\right)=\int_{\mathrm{0}} ^{+\infty} {e}^{−{t}} {ln}\left({t}\right){dt}=−\gamma \\ $$
