Question Number 78708 by abdomathmax last updated on 20/Jan/20
$${calculate}\:\int_{\mathrm{0}} ^{\infty} \:\frac{{e}^{−{x}} }{{x}}\left({sinx}\right)^{\mathrm{2}\:} {dx} \\ $$
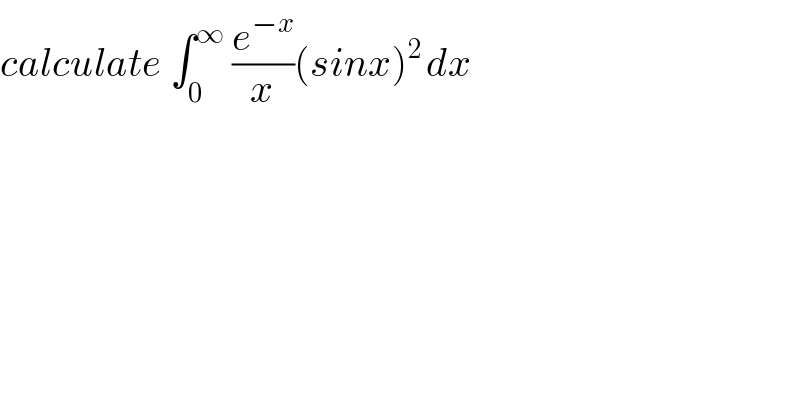
Commented by mathmax by abdo last updated on 21/Jan/20
![let f(t) =∫_0 ^∞ (e^(−xt) /x)sin^2 x dx with t >0 we have f^′ (t) =−∫_0 ^∞ e^(−xt) sin^2 xdx =−∫_0 ^∞ e^(−xt) (1−cos(2x))dx =(1/2)∫_0 ^∞ e^(−xt) cos(2x)dx−(1/2)∫_0 ^∞ e^(−xt) dx ∫_0 ^∞ e^(−xt) dx =[−(1/t)e^(−xt) ]_(x=0) ^∞ =(1/t) ∫_0 ^∞ e^(−xt) cos(2x)dx =Re(∫_0 ^∞ e^(−xt+2ix) dx) ∫_0 ^∞ e^((−t+2i)x) dx =[(1/(−t+2i)) e^((−t+2i)x) ]_0 ^∞ =−(1/(−t+2i)) =(1/(t−2i)) =((t+2i)/(t^2 +4)) ⇒ ∫_0 ^∞ e^(−xt) cos(2x)dx =(t/(t^2 +4)) ⇒2f^′ (t)=(t/(t^2 +4))−(1/t) ⇒ 2f(t) =∫_1 ^t (u/(u^2 +4))−∫_1 ^t (du/u) +c =(1/2)[ln(u^2 +4)]_1 ^t −lnt +c ⇒ f(t)=(1/4){ln(t^2 +4)−ln(5)} −(1/2)ln(t) +c ∃m> /∫_0 ^∞ ∣((e^(−xt) sin^2 x)/x)∣dx≤m∫_0 ^∞ e^(−xt) dx =(m/t)→0(t→+∞) ⇒ lim_(t→+∞) f(t)=0 ⇒lim_(t→+∞) ln((((^4 (√(t^2 +1)))/( (√t)))) −(1/4)ln(5)+c =0 ⇒ c=(1/4)ln(5) ⇒f(t)=(1/4)ln(t^2 +4)−(1/2)ln(t) (t>0) ∫_0 ^∞ (e^(−x) /x)sin^2 x dx =f(1) =((ln(5))/4)](https://www.tinkutara.com/question/Q78943.png)
$${let}\:{f}\left({t}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{e}^{−{xt}} }{{x}}{sin}^{\mathrm{2}} {x}\:{dx}\:\:{with}\:{t}\:>\mathrm{0}\:\:{we}\:{have} \\ $$$${f}^{'} \left({t}\right)\:=−\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−{xt}} {sin}^{\mathrm{2}} {xdx}\:=−\int_{\mathrm{0}} ^{\infty} \:{e}^{−{xt}} \left(\mathrm{1}−{cos}\left(\mathrm{2}{x}\right)\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:{e}^{−{xt}} \:{cos}\left(\mathrm{2}{x}\right){dx}−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:{e}^{−{xt}} \:{dx} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:{e}^{−{xt}} {dx}\:=\left[−\frac{\mathrm{1}}{{t}}{e}^{−{xt}} \right]_{{x}=\mathrm{0}} ^{\infty} \:=\frac{\mathrm{1}}{{t}} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:{e}^{−{xt}} \:{cos}\left(\mathrm{2}{x}\right){dx}\:={Re}\left(\int_{\mathrm{0}} ^{\infty} \:{e}^{−{xt}+\mathrm{2}{ix}} {dx}\right) \\ $$$$\int_{\mathrm{0}} ^{\infty} \:{e}^{\left(−{t}+\mathrm{2}{i}\right){x}} {dx}\:=\left[\frac{\mathrm{1}}{−{t}+\mathrm{2}{i}}\:{e}^{\left(−{t}+\mathrm{2}{i}\right){x}} \right]_{\mathrm{0}} ^{\infty} =−\frac{\mathrm{1}}{−{t}+\mathrm{2}{i}}\:=\frac{\mathrm{1}}{{t}−\mathrm{2}{i}}\:=\frac{{t}+\mathrm{2}{i}}{{t}^{\mathrm{2}} \:+\mathrm{4}}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:{e}^{−{xt}} \:{cos}\left(\mathrm{2}{x}\right){dx}\:=\frac{{t}}{{t}^{\mathrm{2}} \:+\mathrm{4}}\:\Rightarrow\mathrm{2}{f}^{'} \left({t}\right)=\frac{{t}}{{t}^{\mathrm{2}} \:+\mathrm{4}}−\frac{\mathrm{1}}{{t}}\:\Rightarrow \\ $$$$\mathrm{2}{f}\left({t}\right)\:=\int_{\mathrm{1}} ^{{t}} \:\:\frac{{u}}{{u}^{\mathrm{2}} \:+\mathrm{4}}−\int_{\mathrm{1}} ^{{t}} \:\frac{{du}}{{u}}\:+{c}\:=\frac{\mathrm{1}}{\mathrm{2}}\left[{ln}\left({u}^{\mathrm{2}} \:+\mathrm{4}\right)\right]_{\mathrm{1}} ^{{t}} −{lnt}\:\:+{c}\:\Rightarrow \\ $$$$ \\ $$$${f}\left({t}\right)=\frac{\mathrm{1}}{\mathrm{4}}\left\{{ln}\left({t}^{\mathrm{2}} \:+\mathrm{4}\right)−{ln}\left(\mathrm{5}\right)\right\}\:−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({t}\right)\:+{c} \\ $$$$\exists{m}>\:/\int_{\mathrm{0}} ^{\infty} \mid\frac{{e}^{−{xt}} {sin}^{\mathrm{2}} {x}}{{x}}\mid{dx}\leqslant{m}\int_{\mathrm{0}} ^{\infty} {e}^{−{xt}} {dx}\:=\frac{{m}}{{t}}\rightarrow\mathrm{0}\left({t}\rightarrow+\infty\right)\:\Rightarrow \\ $$$${lim}_{{t}\rightarrow+\infty} {f}\left({t}\right)=\mathrm{0}\:\Rightarrow{lim}_{{t}\rightarrow+\infty} {ln}\left(\frac{\left(^{\mathrm{4}} \sqrt{{t}^{\mathrm{2}} \:+\mathrm{1}}\right.}{\:\sqrt{{t}}}\right)\:−\frac{\mathrm{1}}{\mathrm{4}}{ln}\left(\mathrm{5}\right)+{c}\:=\mathrm{0}\:\Rightarrow \\ $$$${c}=\frac{\mathrm{1}}{\mathrm{4}}{ln}\left(\mathrm{5}\right)\:\Rightarrow{f}\left({t}\right)=\frac{\mathrm{1}}{\mathrm{4}}{ln}\left({t}^{\mathrm{2}} \:+\mathrm{4}\right)−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({t}\right)\:\:\left({t}>\mathrm{0}\right) \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{{e}^{−{x}} }{{x}}{sin}^{\mathrm{2}} {x}\:{dx}\:={f}\left(\mathrm{1}\right)\:=\frac{{ln}\left(\mathrm{5}\right)}{\mathrm{4}} \\ $$
Answered by mind is power last updated on 20/Jan/20
![existence in 0 sin^2 (x)∼x^2 e^(−x) x is integrable in ∞ ((sin^2 (x))/x)<1⇒e^(−x) ((sin^2 (x))/x)<e^(−x) obvious let f(t)=∫_0 ^(+∞) (e^(−xt) /x)sin^2 (x)dx,t∈[1,∞[=I f well definde C_∞ in I lim_(t→∞) f(t)=0 proof u=xt⇒∫_0 ^(+∞) (e^(−u) /u)sin^2 ((u/t))du ∣sin((u/t))∣≤(u/t)⇒∫_0 ^(+∞) (e^(−u) /u)sin^2 ((u/t))du≤∫_0 ^(+∞) (e^(−u) /u)(u^2 /t^2 )du=(1/t^2 )∫_0 ^(+∞) ue^(−u) du=((Γ(1))/t^2 ) →0 as t→∞ (∂f/∂t)=∫_0 ^(+∞) −e^(−xt) sin^2 (x)dx=−∫_0 ^(+∞) e^(−xt) (((1−cos(2x))/2))dx =−(1/2)∫_0 ^(+∞) e^(−xt) dx+(1/2)∫_0 ^(+∞) e^(−xt) cos(2x)dx =(1/2)[(e^(−xt) /t)]_0 ^(+∞) +(1/2)Re{∫_0 ^(+∞) e^(x(−t+2i)) dt} =−(1/(2t))+(1/2)Re[(e^(x(−t+2i)) /(−t+2i))]_0 ^(+∞) =−(1/(2t))+(1/2)Re[(1/(t−2i))] =−(1/(2t))+(1/2)(t/(t^2 +4))=f′(t) f(1)=∫_∞ ^1 f′(t)dt=∫_∞ ^1 {−(1/(2t))+(t/(2(t^2 +4)))}dt=lim_(x→∞) [_x ^1 −(1/2)ln(t)+(1/4)ln(t^2 +4)] =lim_(x→∞) [_x ^1 (1/4)ln(((t^2 +4)/t^2 ))]=((ln(5))/4)−lim_(x→∞) ((ln(((x^2 +4)/x^2 )))/4)=((ln(5))/4)](https://www.tinkutara.com/question/Q78768.png)
$$\mathrm{existence}\:\mathrm{in}\:\mathrm{0}\:\mathrm{sin}^{\mathrm{2}} \left(\mathrm{x}\right)\sim\mathrm{x}^{\mathrm{2}} \\ $$$$\mathrm{e}^{−\mathrm{x}} \mathrm{x}\:\:\mathrm{is}\:\mathrm{integrable} \\ $$$$\mathrm{in}\:\infty\:\:\:\frac{\mathrm{sin}^{\mathrm{2}} \left(\mathrm{x}\right)}{\mathrm{x}}<\mathrm{1}\Rightarrow\mathrm{e}^{−\mathrm{x}} \frac{\mathrm{sin}^{\mathrm{2}} \left(\mathrm{x}\right)}{\mathrm{x}}<\mathrm{e}^{−\mathrm{x}} \:\:\mathrm{obvious} \\ $$$$\mathrm{let}\:\mathrm{f}\left(\mathrm{t}\right)=\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{e}^{−\mathrm{xt}} }{\mathrm{x}}\mathrm{sin}^{\mathrm{2}} \left(\mathrm{x}\right)\mathrm{dx},\mathrm{t}\in\left[\mathrm{1},\infty\left[=\mathrm{I}\right.\right. \\ $$$$\mathrm{f}\:\mathrm{well}\:\mathrm{definde}\:\mathrm{C}_{\infty} \:\:\mathrm{in}\:\mathrm{I}\: \\ $$$$\underset{\mathrm{t}\rightarrow\infty} {\mathrm{lim}f}\left(\mathrm{t}\right)=\mathrm{0}\:\:\mathrm{proof} \\ $$$$\mathrm{u}=\mathrm{xt}\Rightarrow\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{e}^{−\mathrm{u}} }{\mathrm{u}}\mathrm{sin}^{\mathrm{2}} \left(\frac{\mathrm{u}}{\mathrm{t}}\right)\mathrm{du} \\ $$$$\mid\mathrm{sin}\left(\frac{\mathrm{u}}{\mathrm{t}}\right)\mid\leqslant\frac{\mathrm{u}}{\mathrm{t}}\Rightarrow\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{e}^{−\mathrm{u}} }{\mathrm{u}}\mathrm{sin}^{\mathrm{2}} \left(\frac{\mathrm{u}}{\mathrm{t}}\right)\mathrm{du}\leqslant\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{e}^{−\mathrm{u}} }{\mathrm{u}}\frac{\mathrm{u}^{\mathrm{2}} }{\mathrm{t}^{\mathrm{2}} }\mathrm{du}=\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }\int_{\mathrm{0}} ^{+\infty} \mathrm{ue}^{−\mathrm{u}} \mathrm{du}=\frac{\Gamma\left(\mathrm{1}\right)}{\mathrm{t}^{\mathrm{2}} } \\ $$$$\rightarrow\mathrm{0}\:\:\mathrm{as}\:\mathrm{t}\rightarrow\infty \\ $$$$\frac{\partial\mathrm{f}}{\partial\mathrm{t}}=\int_{\mathrm{0}} ^{+\infty} −\mathrm{e}^{−\mathrm{xt}} \mathrm{sin}^{\mathrm{2}} \left(\mathrm{x}\right)\mathrm{dx}=−\int_{\mathrm{0}} ^{+\infty} \mathrm{e}^{−\mathrm{xt}} \left(\frac{\mathrm{1}−\mathrm{cos}\left(\mathrm{2x}\right)}{\mathrm{2}}\right)\mathrm{dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{+\infty} \mathrm{e}^{−\mathrm{xt}} \mathrm{dx}+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{+\infty} \mathrm{e}^{−\mathrm{xt}} \mathrm{cos}\left(\mathrm{2x}\right)\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{e}^{−\mathrm{xt}} }{\mathrm{t}}\right]_{\mathrm{0}} ^{+\infty} +\frac{\mathrm{1}}{\mathrm{2}}\mathrm{Re}\left\{\int_{\mathrm{0}} ^{+\infty} \mathrm{e}^{\mathrm{x}\left(−\mathrm{t}+\mathrm{2i}\right)} \mathrm{dt}\right\} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2t}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{Re}\left[\frac{\mathrm{e}^{\mathrm{x}\left(−\mathrm{t}+\mathrm{2i}\right)} }{−\mathrm{t}+\mathrm{2i}}\right]_{\mathrm{0}} ^{+\infty} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2t}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{Re}\left[\frac{\mathrm{1}}{\mathrm{t}−\mathrm{2i}}\right] \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2t}}+\frac{\mathrm{1}}{\mathrm{2}}\frac{\mathrm{t}}{\mathrm{t}^{\mathrm{2}} +\mathrm{4}}=\mathrm{f}'\left(\mathrm{t}\right) \\ $$$$\mathrm{f}\left(\mathrm{1}\right)=\int_{\infty} ^{\mathrm{1}} \mathrm{f}'\left(\mathrm{t}\right)\mathrm{dt}=\int_{\infty} ^{\mathrm{1}} \left\{−\frac{\mathrm{1}}{\mathrm{2t}}+\frac{\mathrm{t}}{\mathrm{2}\left(\mathrm{t}^{\mathrm{2}} +\mathrm{4}\right)}\right\}\mathrm{dt}=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left[_{\mathrm{x}} ^{\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{t}\right)+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\left(\mathrm{t}^{\mathrm{2}} +\mathrm{4}\right)\right] \\ $$$$=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left[_{\mathrm{x}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\left(\frac{\mathrm{t}^{\mathrm{2}} +\mathrm{4}}{\mathrm{t}^{\mathrm{2}} }\right)\right]=\frac{\mathrm{ln}\left(\mathrm{5}\right)}{\mathrm{4}}−\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{ln}\left(\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{4}}{\mathrm{x}^{\mathrm{2}} }\right)}{\mathrm{4}}=\frac{\mathrm{ln}\left(\mathrm{5}\right)}{\mathrm{4}} \\ $$
Commented by mathmax by abdo last updated on 20/Jan/20
$${thank}\:{you}\:{sir}. \\ $$
Commented by mind is power last updated on 21/Jan/20
$$\mathrm{y}'\mathrm{re}\:\mathrm{welcom} \\ $$
Answered by M±th+et£s last updated on 20/Jan/20
![L{sin^2 (x)}=(1/2)L{(1−cos2x)}=(1/2){(1/s)−(s/(s^2 +4))} F(s)=L{((sin^2 x U(x))/x)}=∫_s ^∞ (1/2){(1/s) −(s/(s^2 +4))}ds =(1/2)[ln(s)−(1/2)ln(s^2 +4)]_s ^∞ =(1/4)[ln()]_s ^∞ =((−1)/4) ((s^2 /(s^2 +4))) ∫_0 ^∞ ((sin^2 (x) e^(−x) )/x) = F(1)=−(1/4)ln((1/5))=(1/4) ln(5)](https://www.tinkutara.com/question/Q78795.png)
$${L}\left\{{sin}^{\mathrm{2}} \left({x}\right)\right\}=\frac{\mathrm{1}}{\mathrm{2}}{L}\left\{\left(\mathrm{1}−{cos}\mathrm{2}{x}\right)\right\}=\frac{\mathrm{1}}{\mathrm{2}}\left\{\frac{\mathrm{1}}{{s}}−\frac{{s}}{{s}^{\mathrm{2}} +\mathrm{4}}\right\} \\ $$$${F}\left({s}\right)={L}\left\{\frac{{sin}^{\mathrm{2}} {x}\:{U}\left({x}\right)}{{x}}\right\}=\int_{{s}} ^{\infty} \frac{\mathrm{1}}{\mathrm{2}}\left\{\frac{\mathrm{1}}{{s}}\:−\frac{{s}}{{s}^{\mathrm{2}} +\mathrm{4}}\right\}{ds} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[{ln}\left({s}\right)−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({s}^{\mathrm{2}} +\mathrm{4}\right)\right]_{{s}} ^{\infty} =\frac{\mathrm{1}}{\mathrm{4}}\left[{ln}\left(\right)\right]_{{s}} ^{\infty} \\ $$$$=\frac{−\mathrm{1}}{\mathrm{4}}\:\left(\frac{{s}^{\mathrm{2}} }{{s}^{\mathrm{2}} +\mathrm{4}}\right) \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{sin}^{\mathrm{2}} \left({x}\right)\:{e}^{−{x}} }{{x}}\:=\:{F}\left(\mathrm{1}\right)=−\frac{\mathrm{1}}{\mathrm{4}}{ln}\left(\frac{\mathrm{1}}{\mathrm{5}}\right)=\frac{\mathrm{1}}{\mathrm{4}}\:{ln}\left(\mathrm{5}\right) \\ $$
Commented by M±th+et£s last updated on 20/Jan/20
![so sorry there is a typo (1/4)[ln((s^2 /(s^2 +4)))]_s ^∞](https://www.tinkutara.com/question/Q78796.png)
$${so}\:{sorry}\:{there}\:{is}\:{a}\:{typo} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\left[{ln}\left(\frac{{s}^{\mathrm{2}} }{{s}^{\mathrm{2}} +\mathrm{4}}\right)\right]_{{s}} ^{\infty} \\ $$