Question Number 50418 by Abdo msup. last updated on 16/Dec/18
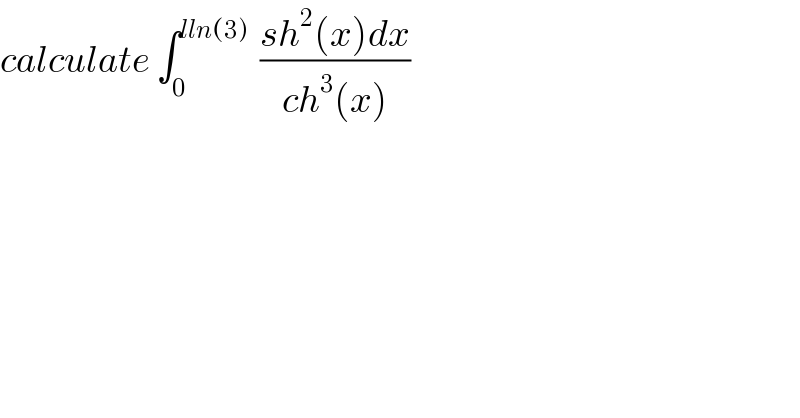
$${calculate}\:\int_{\mathrm{0}} ^{{lln}\left(\mathrm{3}\right)} \:\:\frac{{sh}^{\mathrm{2}} \left({x}\right){dx}}{{ch}^{\mathrm{3}} \left({x}\right)} \\ $$
Commented by Abdo msup. last updated on 24/Dec/18
![let A =∫_0 ^(ln(3)) ((sh^2 (x))/(ch^3 (x)))dx we have A = ∫_0 ^(ln(3)) ((ch^2 x−1)/(ch^3 x))dx =∫_0 ^(ln(3)) (dx/(ch(x))) −∫_0 ^(ln(3)) (dx/(ch^3 x)) ∫_0 ^(ln(3)) (dx/(ch(x))) =∫_0 ^(ln(3)) ((2dx)/(e^x +e^(−x) )) =_(e^x =t) ∫_1 ^3 (2/(t+t^(−1) )) (dt/t) = ∫_1 ^3 ((2dt)/(t^2 +1)) =[2arctan(t)]_1 ^3 =2( arctan(3)−(π/4))=2arctan(3)−(π/2) ∫_0 ^(ln(3)) (dx/(ch^3 x)) =8 ∫_0 ^(ln(3)) (dx/((e^x +e^(−x) )^3 )) =8 ∫_0 ^(ln(3)) (dx/(e^(3x) +3 e^(2x) e^(−x) +3 e^x e^(−2x) +e^(−3x) )) =8 ∫_0 ^(ln(3) ) (dx/(e^(3x) +e^(−3x) +3 e^(x ) +3 e^(−x) )) =_(e^x =t) 8 ∫_1 ^3 (dt/(t(t^3 +t^(−3) +3t +3t^(−1) ))) =8 ∫_1 ^3 (dt/(t^4 +t^(−2) +3t^2 +3)) =8 ∫_1 ^3 ((t^2 dt)/(t^(6 ) +1 +3t^4 +3t^2 )) let decompose F(t) = (t^2 /(t^6 +3t^4 +3t^2 +1)) ....be continued....](https://www.tinkutara.com/question/Q51142.png)
$${let}\:{A}\:=\int_{\mathrm{0}} ^{{ln}\left(\mathrm{3}\right)} \:\:\frac{{sh}^{\mathrm{2}} \left({x}\right)}{{ch}^{\mathrm{3}} \left({x}\right)}{dx}\:\:{we}\:{have} \\ $$$${A}\:=\:\int_{\mathrm{0}} ^{{ln}\left(\mathrm{3}\right)} \:\frac{{ch}^{\mathrm{2}} {x}−\mathrm{1}}{{ch}^{\mathrm{3}} {x}}{dx}\:=\int_{\mathrm{0}} ^{{ln}\left(\mathrm{3}\right)} \:\frac{{dx}}{{ch}\left({x}\right)}\:−\int_{\mathrm{0}} ^{{ln}\left(\mathrm{3}\right)} \:\frac{{dx}}{{ch}^{\mathrm{3}} {x}} \\ $$$$\int_{\mathrm{0}} ^{{ln}\left(\mathrm{3}\right)} \:\:\frac{{dx}}{{ch}\left({x}\right)}\:=\int_{\mathrm{0}} ^{{ln}\left(\mathrm{3}\right)} \:\:\:\frac{\mathrm{2}{dx}}{{e}^{{x}} \:+{e}^{−{x}} }\:=_{{e}^{{x}} ={t}} \:\:\int_{\mathrm{1}} ^{\mathrm{3}} \:\:\:\frac{\mathrm{2}}{{t}+{t}^{−\mathrm{1}} }\:\frac{{dt}}{{t}} \\ $$$$=\:\int_{\mathrm{1}} ^{\mathrm{3}} \:\:\:\frac{\mathrm{2}{dt}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:=\left[\mathrm{2}{arctan}\left({t}\right)\right]_{\mathrm{1}} ^{\mathrm{3}} \\ $$$$=\mathrm{2}\left(\:{arctan}\left(\mathrm{3}\right)−\frac{\pi}{\mathrm{4}}\right)=\mathrm{2}{arctan}\left(\mathrm{3}\right)−\frac{\pi}{\mathrm{2}} \\ $$$$\int_{\mathrm{0}} ^{{ln}\left(\mathrm{3}\right)} \:\:\:\frac{{dx}}{{ch}^{\mathrm{3}} {x}}\:=\mathrm{8}\:\int_{\mathrm{0}} ^{{ln}\left(\mathrm{3}\right)} \:\:\frac{{dx}}{\left({e}^{{x}} \:+{e}^{−{x}} \right)^{\mathrm{3}} } \\ $$$$=\mathrm{8}\:\int_{\mathrm{0}} ^{{ln}\left(\mathrm{3}\right)} \:\:\:\frac{{dx}}{{e}^{\mathrm{3}{x}} \:+\mathrm{3}\:{e}^{\mathrm{2}{x}} \:{e}^{−{x}} \:+\mathrm{3}\:{e}^{{x}} \:{e}^{−\mathrm{2}{x}} \:+{e}^{−\mathrm{3}{x}} } \\ $$$$=\mathrm{8}\:\int_{\mathrm{0}} ^{{ln}\left(\mathrm{3}\right)\:\:\:} \:\:\:\:\:\frac{{dx}}{{e}^{\mathrm{3}{x}} \:\:+{e}^{−\mathrm{3}{x}} \:+\mathrm{3}\:{e}^{{x}\:} \:+\mathrm{3}\:{e}^{−{x}} } \\ $$$$=_{{e}^{{x}} ={t}} \:\mathrm{8}\:\int_{\mathrm{1}} ^{\mathrm{3}} \:\:\:\:\:\:\:\:\frac{{dt}}{{t}\left({t}^{\mathrm{3}} \:+{t}^{−\mathrm{3}} \:+\mathrm{3}{t}\:+\mathrm{3}{t}^{−\mathrm{1}} \right)} \\ $$$$=\mathrm{8}\:\int_{\mathrm{1}} ^{\mathrm{3}} \:\:\:\frac{{dt}}{{t}^{\mathrm{4}} \:+{t}^{−\mathrm{2}} \:+\mathrm{3}{t}^{\mathrm{2}} \:+\mathrm{3}} \\ $$$$=\mathrm{8}\:\int_{\mathrm{1}} ^{\mathrm{3}} \:\:\:\:\frac{{t}^{\mathrm{2}} {dt}}{{t}^{\mathrm{6}\:} \:+\mathrm{1}\:+\mathrm{3}{t}^{\mathrm{4}} \:+\mathrm{3}{t}^{\mathrm{2}} } \\ $$$${let}\:{decompose}\:\:{F}\left({t}\right)\:=\:\frac{{t}^{\mathrm{2}} }{{t}^{\mathrm{6}} \:+\mathrm{3}{t}^{\mathrm{4}} \:+\mathrm{3}{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$….{be}\:{continued}…. \\ $$$$ \\ $$
