Question Number 42505 by maxmathsup by imad last updated on 26/Aug/18
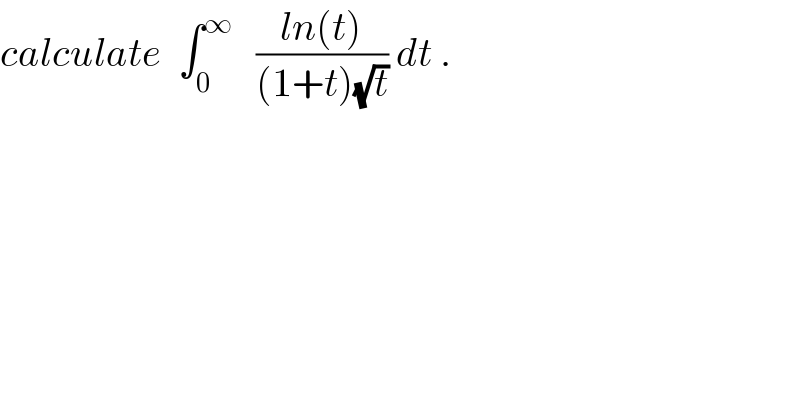
$${calculate}\:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{ln}\left({t}\right)}{\left(\mathrm{1}+{t}\right)\sqrt{{t}}}\:{dt}\:. \\ $$
Commented by maxmathsup by imad last updated on 29/Aug/18
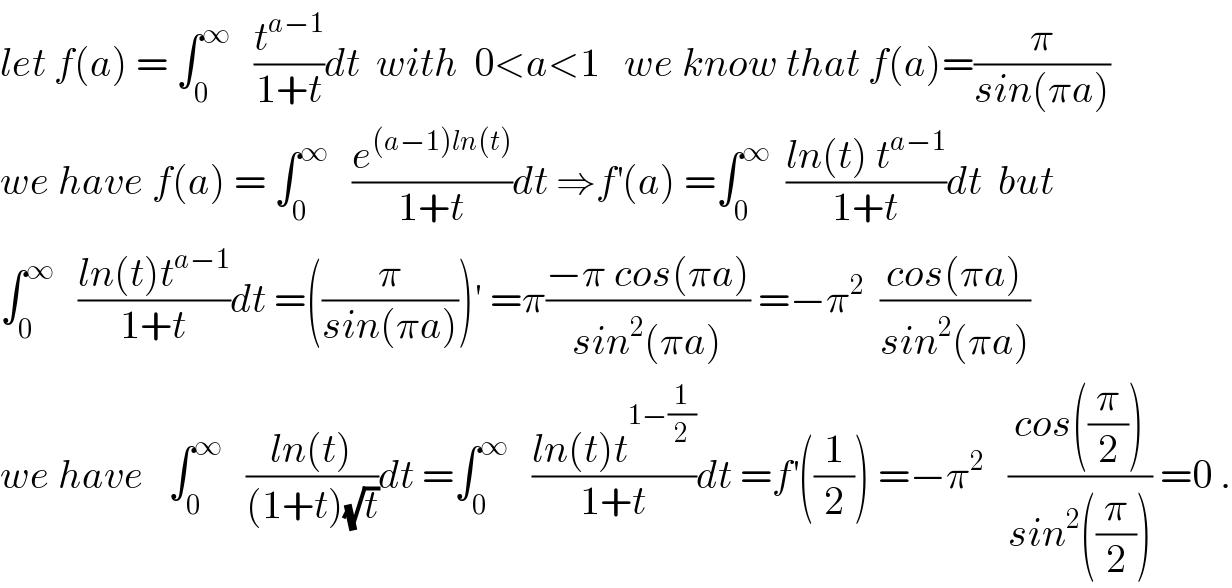
$${let}\:{f}\left({a}\right)\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{t}^{{a}−\mathrm{1}} }{\mathrm{1}+{t}}{dt}\:\:{with}\:\:\mathrm{0}<{a}<\mathrm{1}\:\:\:{we}\:{know}\:{that}\:{f}\left({a}\right)=\frac{\pi}{{sin}\left(\pi{a}\right)} \\ $$$${we}\:{have}\:{f}\left({a}\right)\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{e}^{\left({a}−\mathrm{1}\right){ln}\left({t}\right)} }{\mathrm{1}+{t}}{dt}\:\Rightarrow{f}^{'} \left({a}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{ln}\left({t}\right)\:{t}^{{a}−\mathrm{1}} }{\mathrm{1}+{t}}{dt}\:\:{but} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{ln}\left({t}\right){t}^{{a}−\mathrm{1}} }{\mathrm{1}+{t}}{dt}\:=\left(\frac{\pi}{{sin}\left(\pi{a}\right)}\right)'\:=\pi\frac{−\pi\:{cos}\left(\pi{a}\right)}{{sin}^{\mathrm{2}} \left(\pi{a}\right)}\:=−\pi^{\mathrm{2}} \:\:\frac{{cos}\left(\pi{a}\right)}{{sin}^{\mathrm{2}} \left(\pi{a}\right)} \\ $$$${we}\:{have}\:\:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{ln}\left({t}\right)}{\left(\mathrm{1}+{t}\right)\sqrt{{t}}}{dt}\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{ln}\left({t}\right){t}^{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}} }{\mathrm{1}+{t}}{dt}\:={f}^{'} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:=−\pi^{\mathrm{2}} \:\:\:\frac{{cos}\left(\frac{\pi}{\mathrm{2}}\right)}{{sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{2}}\right)}\:=\mathrm{0}\:. \\ $$
Commented by maxmathsup by imad last updated on 29/Aug/18
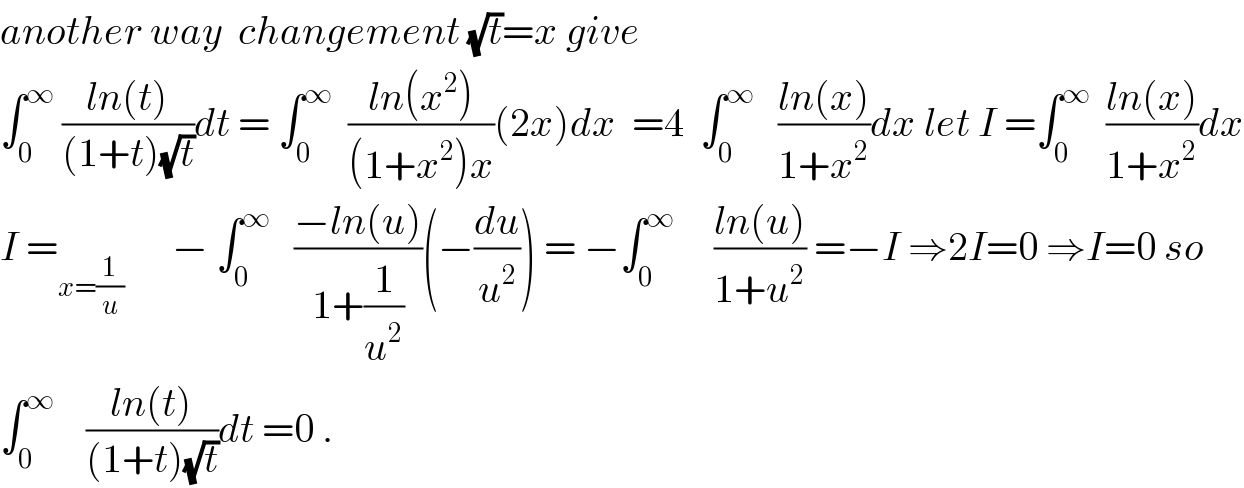
$${another}\:{way}\:\:{changement}\:\sqrt{{t}}={x}\:{give} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\frac{{ln}\left({t}\right)}{\left(\mathrm{1}+{t}\right)\sqrt{{t}}}{dt}\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{ln}\left({x}^{\mathrm{2}} \right)}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right){x}}\left(\mathrm{2}{x}\right){dx}\:\:=\mathrm{4}\:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{ln}\left({x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:{let}\:{I}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{ln}\left({x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$${I}\:=_{{x}=\frac{\mathrm{1}}{{u}}} \:\:\:\:\:\:−\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{−{ln}\left({u}\right)}{\mathrm{1}+\frac{\mathrm{1}}{{u}^{\mathrm{2}} }}\left(−\frac{{du}}{{u}^{\mathrm{2}} }\right)\:=\:−\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\frac{{ln}\left({u}\right)}{\mathrm{1}+{u}^{\mathrm{2}} }\:=−{I}\:\Rightarrow\mathrm{2}{I}=\mathrm{0}\:\Rightarrow{I}=\mathrm{0}\:{so} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{ln}\left({t}\right)}{\left(\mathrm{1}+{t}\right)\sqrt{{t}}}{dt}\:=\mathrm{0}\:. \\ $$
