Question Number 55457 by maxmathsup by imad last updated on 24/Feb/19
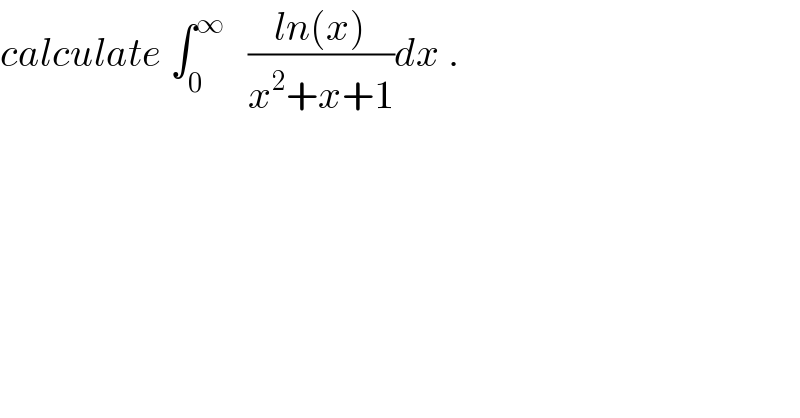
$${calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{ln}\left({x}\right)}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{dx}\:. \\ $$
Commented by maxmathsup by imad last updated on 05/Mar/19
![let I =∫_0 ^∞ ((ln(x))/(x^2 +x+1))dx ⇒I =∫_0 ^∞ ((lnx)/((x+(1/2))^2 +(3/4)))dx =_(x+(1/2)=((√3)/2)t) ∫_(1/( (√3))) ^(+∞) ((ln(((√3)/2)t−(1/2)))/((3/4)(1+t^2 ))) ((√3)/2)dt =(4/3) ((√3)/2) ∫_(1/( (√3))) ^(+∞) ((ln(((√3)/2)t−(1/2)))/(1+t^2 ))dt =(2/( (√3))) ∫_(1/( (√3))) ^(+∞) ((ln(((√3)/2)t−(1/2)))/(t^2 +1))dt ⇒ I =(2/( (√3))) ∫_(1/( (√3))) ^(+∞) ((ln(((√3)/2)x−(1/2)))/(x^2 +1))dx let f(t) =∫_(1/( (√3))) ^(+∞) ((ln(tx−1))/(x^2 +1))dx ⇒f^′ (t) =∫_(1/( (√3))) ^(+∞) (x/((tx−1)(x^2 +1)))dx let decompise F(x) =(x/((tx−1)(x^2 +1))) ⇒F(x)=(a/(tx−1)) +((bx +c)/(x^2 +1)) a =lim_(x→(1/t)) (tx−1)F(x) =(1/(t((1/t^2 ) +1))) =(1/(t+(1/t))) =(t/(t^2 +1)) lim_(x→+∞) xF(x)=(a/t) +b =0 ⇒b =−(a/t) =−(1/(t^2 +1)) ⇒ F(x) =(t/((t^2 +1)(tx−1))) +((−(1/(t^2 +1))x+c)/(x^2 +1)) F(0) =0 =−(t/(t^2 +1)) +c ⇒c =(t/(t^2 +1)) ⇒ F(x) =(t/((t^2 +1)(tx−1))) +(1/(t^2 +1)) ((−x+t)/(x^2 +1)) ⇒ ∫ F(x)dx =(1/(t^2 +1))ln∣tx−1∣−(1/(2(t^2 +1)))ln(x^2 +1) +(t/(t^2 +1)) arctan(x) +c ⇒ ∫_(1/( (√3))) ^(+∞) F(x)dx =(1/(t^2 +1))[ln∣((tx−1)/( (√(x^2 +1))))∣]_(1/( (√3))) ^(+∞) +(t/(t^2 +1))[arctant]_(1/( (√3))) ^(+∞) =(1/(t^2 +1)){ln∣t∣−ln∣(((t/( (√3)))−1)/(2/( (√3))))∣} +(t/(t^2 +1)){(π/2) −(π/6)} =(1/(t^2 +1)){ln∣t∣−ln∣((t−(√3))/2)∣} +((πt)/(3(t^2 +1))) =f^′ (t) ⇒ f(t) =∫ ((ln∣t∣)/(t^2 +1))dt−∫ ((ln∣t−(√3))−ln(2))/(t^2 +1)) dt +(π/6)ln(t^2 +1) +C =∫ ((ln∣t∣)/(t^2 +1))dt −∫((ln∣t−(√3)∣)/(t^2 +1))dt+ln(2)arctant +C ....be continued....](https://www.tinkutara.com/question/Q55896.png)
$${let}\:{I}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{{ln}\left({x}\right)}{{x}^{\mathrm{2}} \:+{x}+\mathrm{1}}{dx}\:\:\:\Rightarrow{I}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{{lnx}}{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{3}}{\mathrm{4}}}{dx} \\ $$$$=_{{x}+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{t}} \:\:\:\:\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} ^{+\infty} \:\frac{{ln}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{t}−\frac{\mathrm{1}}{\mathrm{2}}\right)}{\frac{\mathrm{3}}{\mathrm{4}}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{dt}\:=\frac{\mathrm{4}}{\mathrm{3}}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} ^{+\infty} \:\:\frac{{ln}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{t}−\frac{\mathrm{1}}{\mathrm{2}}\right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\:\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} ^{+\infty} \:\:\frac{{ln}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{t}−\frac{\mathrm{1}}{\mathrm{2}}\right)}{{t}^{\mathrm{2}} \:+\mathrm{1}}{dt}\:\Rightarrow\:{I}\:=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\:\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} ^{+\infty} \:\:\frac{{ln}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{x}−\frac{\mathrm{1}}{\mathrm{2}}\right)}{{x}^{\mathrm{2}} \:+\mathrm{1}}{dx}\:{let}\: \\ $$$${f}\left({t}\right)\:=\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} ^{+\infty} \:\:\frac{{ln}\left({tx}−\mathrm{1}\right)}{{x}^{\mathrm{2}} \:+\mathrm{1}}{dx}\:\Rightarrow{f}^{'} \left({t}\right)\:=\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} ^{+\infty} \:\:\:\:\frac{{x}}{\left({tx}−\mathrm{1}\right)\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)}{dx}\:{let}\:{decompise} \\ $$$${F}\left({x}\right)\:=\frac{{x}}{\left({tx}−\mathrm{1}\right)\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)}\:\Rightarrow{F}\left({x}\right)=\frac{{a}}{{tx}−\mathrm{1}}\:+\frac{{bx}\:+{c}}{{x}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${a}\:={lim}_{{x}\rightarrow\frac{\mathrm{1}}{{t}}} \:\:\:\left({tx}−\mathrm{1}\right){F}\left({x}\right)\:=\frac{\mathrm{1}}{{t}\left(\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\:+\mathrm{1}\right)}\:=\frac{\mathrm{1}}{{t}+\frac{\mathrm{1}}{{t}}}\:=\frac{{t}}{{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${lim}_{{x}\rightarrow+\infty} {xF}\left({x}\right)=\frac{{a}}{{t}}\:+{b}\:=\mathrm{0}\:\Rightarrow{b}\:=−\frac{{a}}{{t}}\:=−\frac{\mathrm{1}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow \\ $$$${F}\left({x}\right)\:=\frac{{t}}{\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)\left({tx}−\mathrm{1}\right)}\:+\frac{−\frac{\mathrm{1}}{{t}^{\mathrm{2}} \:+\mathrm{1}}{x}+{c}}{{x}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${F}\left(\mathrm{0}\right)\:=\mathrm{0}\:=−\frac{{t}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:+{c}\:\Rightarrow{c}\:=\frac{{t}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow \\ $$$${F}\left({x}\right)\:=\frac{{t}}{\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)\left({tx}−\mathrm{1}\right)}\:+\frac{\mathrm{1}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:\frac{−{x}+{t}}{{x}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow \\ $$$$\int\:{F}\left({x}\right){dx}\:=\frac{\mathrm{1}}{{t}^{\mathrm{2}} \:+\mathrm{1}}{ln}\mid{tx}−\mathrm{1}\mid−\frac{\mathrm{1}}{\mathrm{2}\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)}{ln}\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)\:+\frac{{t}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:{arctan}\left({x}\right)\:+{c}\:\Rightarrow \\ $$$$\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} ^{+\infty} \:{F}\left({x}\right){dx}\:=\frac{\mathrm{1}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\left[{ln}\mid\frac{{tx}−\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} \:+\mathrm{1}}}\mid\right]_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} ^{+\infty} \:\:+\frac{{t}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\left[{arctant}\right]_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} ^{+\infty} \\ $$$$=\frac{\mathrm{1}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\left\{{ln}\mid{t}\mid−{ln}\mid\frac{\frac{{t}}{\:\sqrt{\mathrm{3}}}−\mathrm{1}}{\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}}\mid\right\}\:+\frac{{t}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\left\{\frac{\pi}{\mathrm{2}}\:−\frac{\pi}{\mathrm{6}}\right\} \\ $$$$=\frac{\mathrm{1}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\left\{{ln}\mid{t}\mid−{ln}\mid\frac{{t}−\sqrt{\mathrm{3}}}{\mathrm{2}}\mid\right\}\:+\frac{\pi{t}}{\mathrm{3}\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)}\:={f}^{'} \left({t}\right)\:\Rightarrow \\ $$$${f}\left({t}\right)\:=\int\:\frac{{ln}\mid{t}\mid}{{t}^{\mathrm{2}} \:+\mathrm{1}}{dt}−\int\:\:\frac{\left.{ln}\mid{t}−\sqrt{\mathrm{3}}\right)−{ln}\left(\mathrm{2}\right)}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:{dt}\:\:+\frac{\pi}{\mathrm{6}}{ln}\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)\:+{C} \\ $$$$=\int\:\:\frac{{ln}\mid{t}\mid}{{t}^{\mathrm{2}} \:+\mathrm{1}}{dt}\:\:\:−\int\frac{{ln}\mid{t}−\sqrt{\mathrm{3}}\mid}{{t}^{\mathrm{2}} \:+\mathrm{1}}{dt}+{ln}\left(\mathrm{2}\right){arctant}\:+{C}\:….{be}\:{continued}…. \\ $$
Commented by Abdo msup. last updated on 05/Mar/19
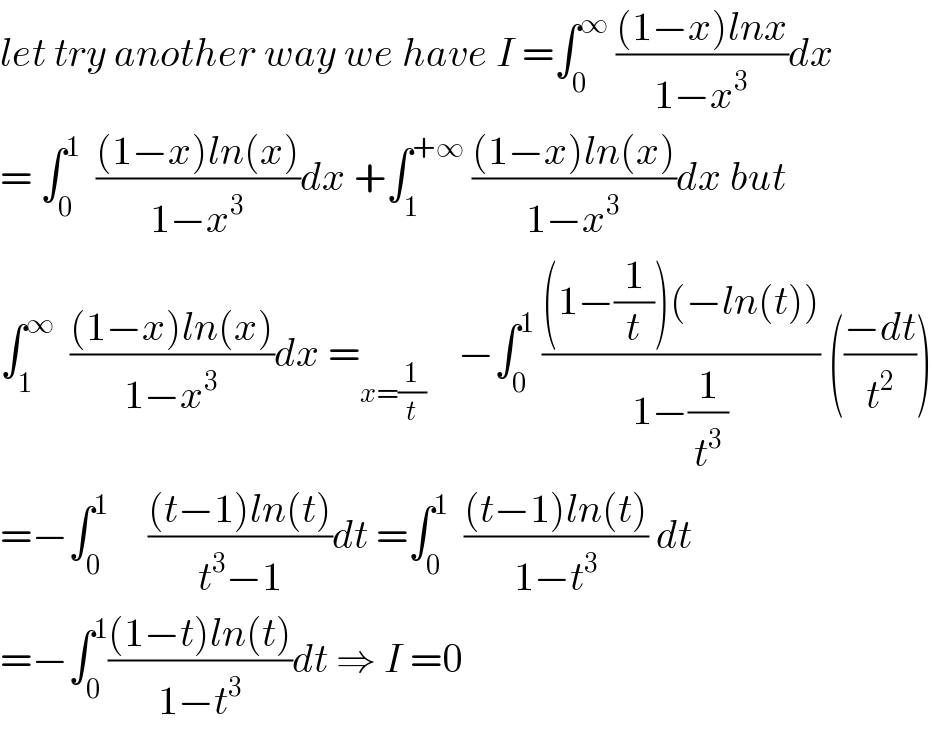
$${let}\:{try}\:{another}\:{way}\:{we}\:{have}\:{I}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\left(\mathrm{1}−{x}\right){lnx}}{\mathrm{1}−{x}^{\mathrm{3}} }{dx} \\ $$$$=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\left(\mathrm{1}−{x}\right){ln}\left({x}\right)}{\mathrm{1}−{x}^{\mathrm{3}} }{dx}\:+\int_{\mathrm{1}} ^{+\infty} \:\frac{\left(\mathrm{1}−{x}\right){ln}\left({x}\right)}{\mathrm{1}−{x}^{\mathrm{3}} }{dx}\:{but} \\ $$$$\int_{\mathrm{1}} ^{\infty} \:\:\frac{\left(\mathrm{1}−{x}\right){ln}\left({x}\right)}{\mathrm{1}−{x}^{\mathrm{3}} }{dx}\:=_{{x}=\frac{\mathrm{1}}{{t}}} \:\:\:\:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\left(\mathrm{1}−\frac{\mathrm{1}}{{t}}\right)\left(−{ln}\left({t}\right)\right)}{\mathrm{1}−\frac{\mathrm{1}}{{t}^{\mathrm{3}} }}\:\left(\frac{−{dt}}{{t}^{\mathrm{2}} }\right) \\ $$$$=−\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\:\frac{\left({t}−\mathrm{1}\right){ln}\left({t}\right)}{{t}^{\mathrm{3}} −\mathrm{1}}{dt}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\left({t}−\mathrm{1}\right){ln}\left({t}\right)}{\mathrm{1}−{t}^{\mathrm{3}} }\:{dt} \\ $$$$=−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(\mathrm{1}−{t}\right){ln}\left({t}\right)}{\mathrm{1}−{t}^{\mathrm{3}} }{dt}\:\Rightarrow\:{I}\:=\mathrm{0} \\ $$
