Menu Close

calculate-0-lnx-1-x-2-2-dx-

Tinku Tara 0 Comments
Pin




Question Number 82755 by mathmax by abdo last updated on 23/Feb/20
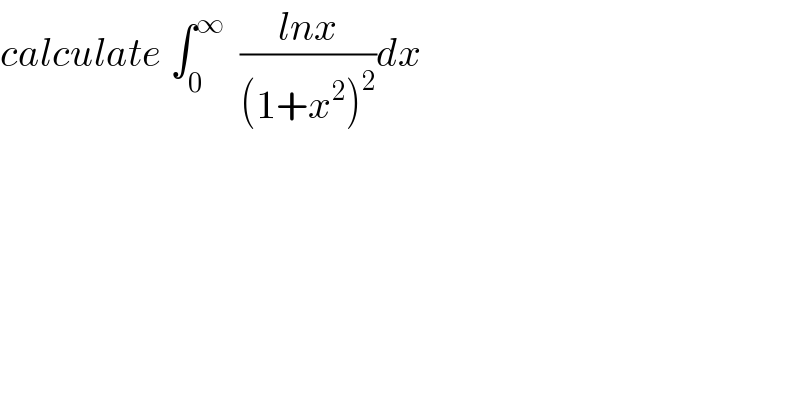
calculate ∫_0 ^∞ ((lnx)/((1+x^2 )^2 ))dx
$${calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{lnx}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx} \\ $$
Commented by Ajao yinka last updated on 24/Feb/20
0
Commented by mathmax by abdo last updated on 24/Feb/20
let f(a) =∫_0 ^∞ ((lnx)/(a+x^2 ))dx with a>0 we can verify eazly that f is derivable on ]0,+∞[ and f^′ (a) =−∫_0 ^∞ ((lnx)/((a+x^2 )^2 ))dx ⇒ ∫_0 ^∞ ((lnx)/((a+x^2 )^2 ))dx =−f^′ (a) let explicit f changement x=(√a)t give f(a) =∫_0 ^∞ ((ln((√a)t))/(a(1+t^2 )))(√a)dt =(1/( (√a)))∫_0 ^∞ (((1/2)lna +lnt)/(t^2 +1))dt =(1/2)((lna)/( (√a)))×(π/2) +(1/( (√a)))∫_0 ^∞ ((lnt)/(1+t^2 ))dt but ∫_0 ^∞ ((ln(t))/(1+t^2 ))dt =0((put t=(1/u)) ⇒ f(a) =((πlna)/(4(√a))) ⇒f^′ (a) =(π/4){((((√a)/a)−lna ×(1/(2(√a))))/a)} =(π/(4a(√a)))−(π/4)×((lna)/(2a(√a))) ⇒∫_0 ^∞ ((lnx)/((a+x^2 )^2 ))dx =−(π/(4a(√a)))+((πlna)/(8a(√a))) a=1 ⇒∫_0 ^∞ ((lnx)/((1+x^2 )^2 ))dx =−(π/4)
$${let}\:{f}\left({a}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{lnx}}{{a}+{x}^{\mathrm{2}} }{dx}\:\:{with}\:{a}>\mathrm{0}\:\:{we}\:{can}\:{verify}\:{eazly}\:{that}\:{f}\:{is} \\ $$$$\left.{derivable}\:{on}\:\right]\mathrm{0},+\infty\left[\:{and}\:{f}^{'} \left({a}\right)\:=−\int_{\mathrm{0}} ^{\infty} \:\frac{{lnx}}{\left({a}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx}\:\Rightarrow\right. \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\frac{{lnx}}{\left({a}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx}\:=−{f}^{'} \left({a}\right)\:{let}\:{explicit}\:{f}\:{changement}\:{x}=\sqrt{{a}}{t}\:{give} \\ $$$${f}\left({a}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\frac{{ln}\left(\sqrt{{a}}{t}\right)}{{a}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}\sqrt{{a}}{dt}\:=\frac{\mathrm{1}}{\:\sqrt{{a}}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\frac{\mathrm{1}}{\mathrm{2}}{lna}\:+{lnt}}{{t}^{\mathrm{2}} \:+\mathrm{1}}{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\frac{{lna}}{\:\sqrt{{a}}}×\frac{\pi}{\mathrm{2}}\:+\frac{\mathrm{1}}{\:\sqrt{{a}}}\int_{\mathrm{0}} ^{\infty} \:\frac{{lnt}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\:{but}\:\int_{\mathrm{0}} ^{\infty} \:\frac{{ln}\left({t}\right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\:=\mathrm{0}\left(\left({put}\:{t}=\frac{\mathrm{1}}{{u}}\right)\:\Rightarrow\right. \\ $$$${f}\left({a}\right)\:=\frac{\pi{lna}}{\mathrm{4}\sqrt{{a}}}\:\Rightarrow{f}^{'} \left({a}\right)\:=\frac{\pi}{\mathrm{4}}\left\{\frac{\frac{\sqrt{{a}}}{{a}}−{lna}\:×\frac{\mathrm{1}}{\mathrm{2}\sqrt{{a}}}}{{a}}\right\} \\ $$$$=\frac{\pi}{\mathrm{4}{a}\sqrt{{a}}}−\frac{\pi}{\mathrm{4}}×\frac{{lna}}{\mathrm{2}{a}\sqrt{{a}}}\:\Rightarrow\int_{\mathrm{0}} ^{\infty} \frac{{lnx}}{\left({a}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx}\:=−\frac{\pi}{\mathrm{4}{a}\sqrt{{a}}}+\frac{\pi{lna}}{\mathrm{8}{a}\sqrt{{a}}} \\ $$$${a}=\mathrm{1}\:\Rightarrow\int_{\mathrm{0}} ^{\infty} \:\:\frac{{lnx}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx}\:=−\frac{\pi}{\mathrm{4}} \\ $$
Answered by mind is power last updated on 24/Feb/20
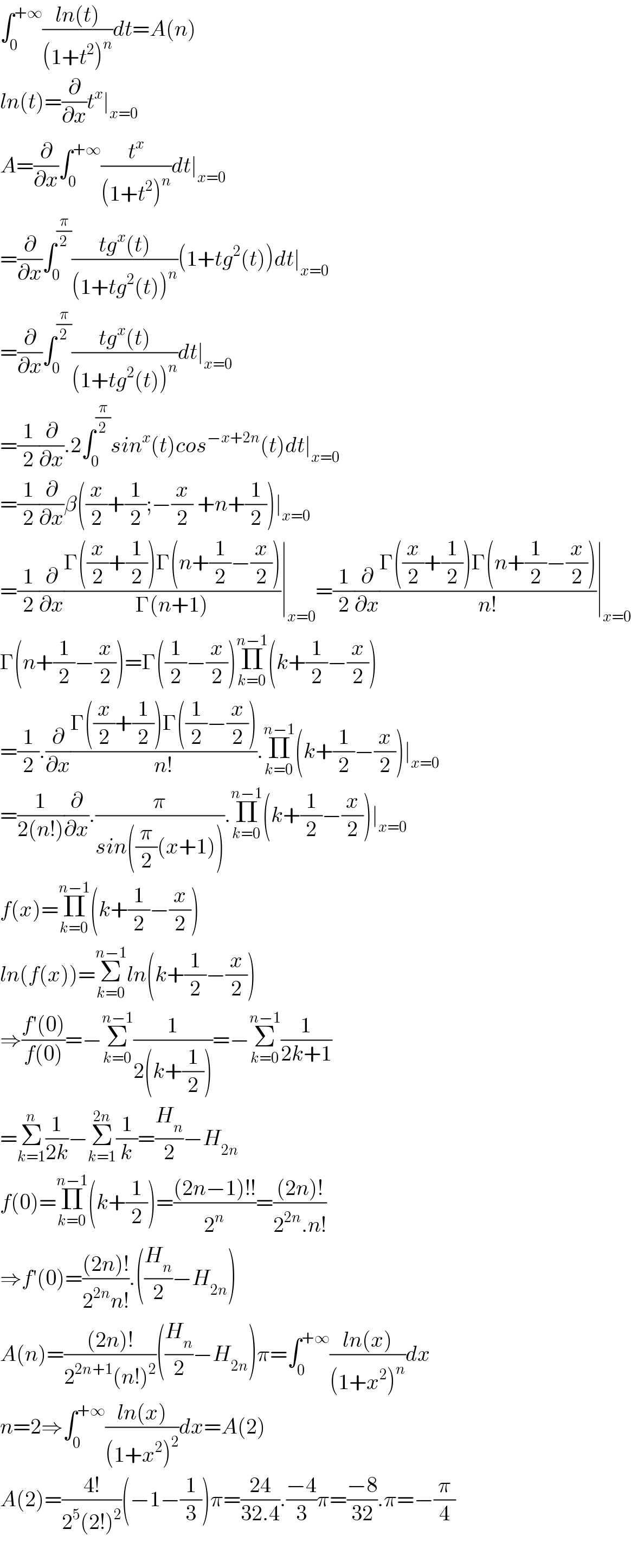
∫_0 ^(+∞) ((ln(t))/((1+t^2 )^n ))dt=A(n) ln(t)=(∂/∂x)t^x ∣_(x=0) A=(∂/∂x)∫_0 ^(+∞) (t^x /((1+t^2 )^n ))dt∣_(x=0) =(∂/∂x)∫_0 ^(π/2) ((tg^x (t))/((1+tg^2 (t))^n ))(1+tg^2 (t))dt∣_(x=0) =(∂/∂x)∫_0 ^(π/2) ((tg^x (t))/((1+tg^2 (t))^n ))dt∣_(x=0) =(1/2)(∂/∂x).2∫_0 ^(π/2) sin^x (t)cos^(−x+2n) (t)dt∣_(x=0) =(1/2)(∂/∂x)β((x/2)+(1/2);−(x/2) +n+(1/2))∣_(x=0) =(1/2)(∂/∂x)((Γ((x/2)+(1/2))Γ(n+(1/2)−(x/2)))/(Γ(n+1)))∣_(x=0) =(1/2)(∂/∂x)((Γ((x/2)+(1/2))Γ(n+(1/2)−(x/2)))/(n!))∣_(x=0) Γ(n+(1/2)−(x/2))=Γ((1/2)−(x/2))Π_(k=0) ^(n−1) (k+(1/2)−(x/2)) =(1/2).(∂/∂x)((Γ((x/2)+(1/2))Γ((1/2)−(x/2)))/(n!)).Π_(k=0) ^(n−1) (k+(1/2)−(x/2))∣_(x=0) =(1/(2(n!)))(∂/∂x).(π/(sin((π/2)(x+1)))).Π_(k=0) ^(n−1) (k+(1/2)−(x/2))∣_(x=0) f(x)=Π_(k=0) ^(n−1) (k+(1/2)−(x/2)) ln(f(x))=Σ_(k=0) ^(n−1) ln(k+(1/2)−(x/2)) ⇒((f′(0))/(f(0)))=−Σ_(k=0) ^(n−1) (1/(2(k+(1/2))))=−Σ_(k=0) ^(n−1) (1/(2k+1)) =Σ_(k=1) ^n (1/(2k))−Σ_(k=1) ^(2n) (1/k)=(H_n /2)−H_(2n) f(0)=Π_(k=0) ^(n−1) (k+(1/2))=(((2n−1)!!)/2^n )=(((2n)!)/(2^(2n) .n!)) ⇒f′(0)=(((2n)!)/(2^(2n) n!)).((H_n /2)−H_(2n) ) A(n)=(((2n)!)/(2^(2n+1) (n!)^2 ))((H_n /2)−H_(2n) )π=∫_0 ^(+∞) ((ln(x))/((1+x^2 )^n ))dx n=2⇒∫_0 ^(+∞) ((ln(x))/((1+x^2 )^2 ))dx=A(2) A(2)=((4!)/(2^5 (2!)^2 ))(−1−(1/3))π=((24)/(32.4)).((−4)/3)π=((−8)/(32)).π=−(π/4)
$$\int_{\mathrm{0}} ^{+\infty} \frac{{ln}\left({t}\right)}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{{n}} }{dt}={A}\left({n}\right) \\ $$$${ln}\left({t}\right)=\frac{\partial}{\partial{x}}{t}^{{x}} \mid_{{x}=\mathrm{0}} \\ $$$${A}=\frac{\partial}{\partial{x}}\int_{\mathrm{0}} ^{+\infty} \frac{{t}^{{x}} }{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{{n}} }{dt}\mid_{{x}=\mathrm{0}} \\ $$$$=\frac{\partial}{\partial{x}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{tg}^{{x}} \left({t}\right)}{\left(\mathrm{1}+{tg}^{\mathrm{2}} \left({t}\right)\right)^{{n}} }\left(\mathrm{1}+{tg}^{\mathrm{2}} \left({t}\right)\right){dt}\mid_{{x}=\mathrm{0}} \\ $$$$=\frac{\partial}{\partial{x}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{tg}^{{x}} \left({t}\right)}{\left(\mathrm{1}+{tg}^{\mathrm{2}} \left({t}\right)\right)^{{n}} }{dt}\mid_{{x}=\mathrm{0}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\frac{\partial}{\partial{x}}.\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sin}^{{x}} \left({t}\right){cos}^{−{x}+\mathrm{2}{n}} \left({t}\right){dt}\mid_{{x}=\mathrm{0}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\frac{\partial}{\partial{x}}\beta\left(\frac{{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}};−\frac{{x}}{\mathrm{2}}\:+{n}+\frac{\mathrm{1}}{\mathrm{2}}\right)\mid_{{x}=\mathrm{0}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\frac{\partial}{\partial{x}}\frac{\Gamma\left(\frac{{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\right)\Gamma\left({n}+\frac{\mathrm{1}}{\mathrm{2}}−\frac{{x}}{\mathrm{2}}\right)}{\Gamma\left({n}+\mathrm{1}\right)}\mid_{{x}=\mathrm{0}} =\frac{\mathrm{1}}{\mathrm{2}}\frac{\partial}{\partial{x}}\frac{\Gamma\left(\frac{{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\right)\Gamma\left({n}+\frac{\mathrm{1}}{\mathrm{2}}−\frac{{x}}{\mathrm{2}}\right)}{{n}!}\mid_{{x}=\mathrm{0}} \\ $$$$\Gamma\left({n}+\frac{\mathrm{1}}{\mathrm{2}}−\frac{{x}}{\mathrm{2}}\right)=\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{{x}}{\mathrm{2}}\right)\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\prod}}\left({k}+\frac{\mathrm{1}}{\mathrm{2}}−\frac{{x}}{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}.\frac{\partial}{\partial{x}}\frac{\Gamma\left(\frac{{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{{x}}{\mathrm{2}}\right)}{{n}!}.\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\prod}}\left({k}+\frac{\mathrm{1}}{\mathrm{2}}−\frac{{x}}{\mathrm{2}}\right)\mid_{{x}=\mathrm{0}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\left({n}!\right)}\frac{\partial}{\partial{x}}.\frac{\pi}{{sin}\left(\frac{\pi}{\mathrm{2}}\left({x}+\mathrm{1}\right)\right)}.\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\prod}}\left({k}+\frac{\mathrm{1}}{\mathrm{2}}−\frac{{x}}{\mathrm{2}}\right)\mid_{{x}=\mathrm{0}} \\ $$$${f}\left({x}\right)=\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\prod}}\left({k}+\frac{\mathrm{1}}{\mathrm{2}}−\frac{{x}}{\mathrm{2}}\right) \\ $$$${ln}\left({f}\left({x}\right)\right)=\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}{ln}\left({k}+\frac{\mathrm{1}}{\mathrm{2}}−\frac{{x}}{\mathrm{2}}\right) \\ $$$$\Rightarrow\frac{{f}'\left(\mathrm{0}\right)}{{f}\left(\mathrm{0}\right)}=−\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\frac{\mathrm{1}}{\mathrm{2}\left({k}+\frac{\mathrm{1}}{\mathrm{2}}\right)}=−\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\frac{\mathrm{1}}{\mathrm{2}{k}+\mathrm{1}} \\ $$$$=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{2}{k}}−\underset{{k}=\mathrm{1}} {\overset{\mathrm{2}{n}} {\sum}}\frac{\mathrm{1}}{{k}}=\frac{{H}_{{n}} }{\mathrm{2}}−{H}_{\mathrm{2}{n}} \\ $$$${f}\left(\mathrm{0}\right)=\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\prod}}\left({k}+\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\left(\mathrm{2}{n}−\mathrm{1}\right)!!}{\mathrm{2}^{{n}} }=\frac{\left(\mathrm{2}{n}\right)!}{\mathrm{2}^{\mathrm{2}{n}} .{n}!} \\ $$$$\Rightarrow{f}'\left(\mathrm{0}\right)=\frac{\left(\mathrm{2}{n}\right)!}{\mathrm{2}^{\mathrm{2}{n}} {n}!}.\left(\frac{{H}_{{n}} }{\mathrm{2}}−{H}_{\mathrm{2}{n}} \right) \\ $$$${A}\left({n}\right)=\frac{\left(\mathrm{2}{n}\right)!}{\mathrm{2}^{\mathrm{2}{n}+\mathrm{1}} \left({n}!\right)^{\mathrm{2}} }\left(\frac{{H}_{{n}} }{\mathrm{2}}−{H}_{\mathrm{2}{n}} \right)\pi=\int_{\mathrm{0}} ^{+\infty} \frac{{ln}\left({x}\right)}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{{n}} }{dx} \\ $$$${n}=\mathrm{2}\Rightarrow\int_{\mathrm{0}} ^{+\infty} \frac{{ln}\left({x}\right)}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx}={A}\left(\mathrm{2}\right) \\ $$$${A}\left(\mathrm{2}\right)=\frac{\mathrm{4}!}{\mathrm{2}^{\mathrm{5}} \left(\mathrm{2}!\right)^{\mathrm{2}} }\left(−\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}\right)\pi=\frac{\mathrm{24}}{\mathrm{32}.\mathrm{4}}.\frac{−\mathrm{4}}{\mathrm{3}}\pi=\frac{−\mathrm{8}}{\mathrm{32}}.\pi=−\frac{\pi}{\mathrm{4}} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *