Menu Close

calculate-0-lnx-x-2-x-2-2-dx-

Tinku Tara 0 Comments
Pin




Question Number 115725 by Bird last updated on 28/Sep/20
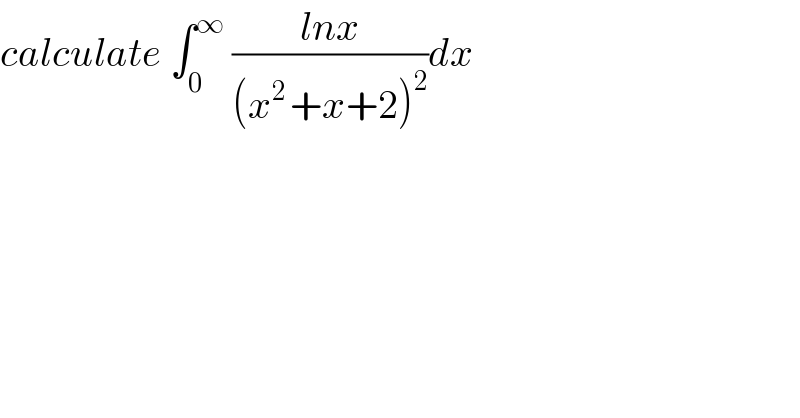
calculate ∫_0 ^∞ ((lnx)/((x^(2 ) +x+2)^2 ))dx
$${calculate}\:\int_{\mathrm{0}} ^{\infty} \:\frac{{lnx}}{\left({x}^{\mathrm{2}\:} +{x}+\mathrm{2}\right)^{\mathrm{2}} }{dx} \\ $$
Answered by mathmax by abdo last updated on 28/Sep/20
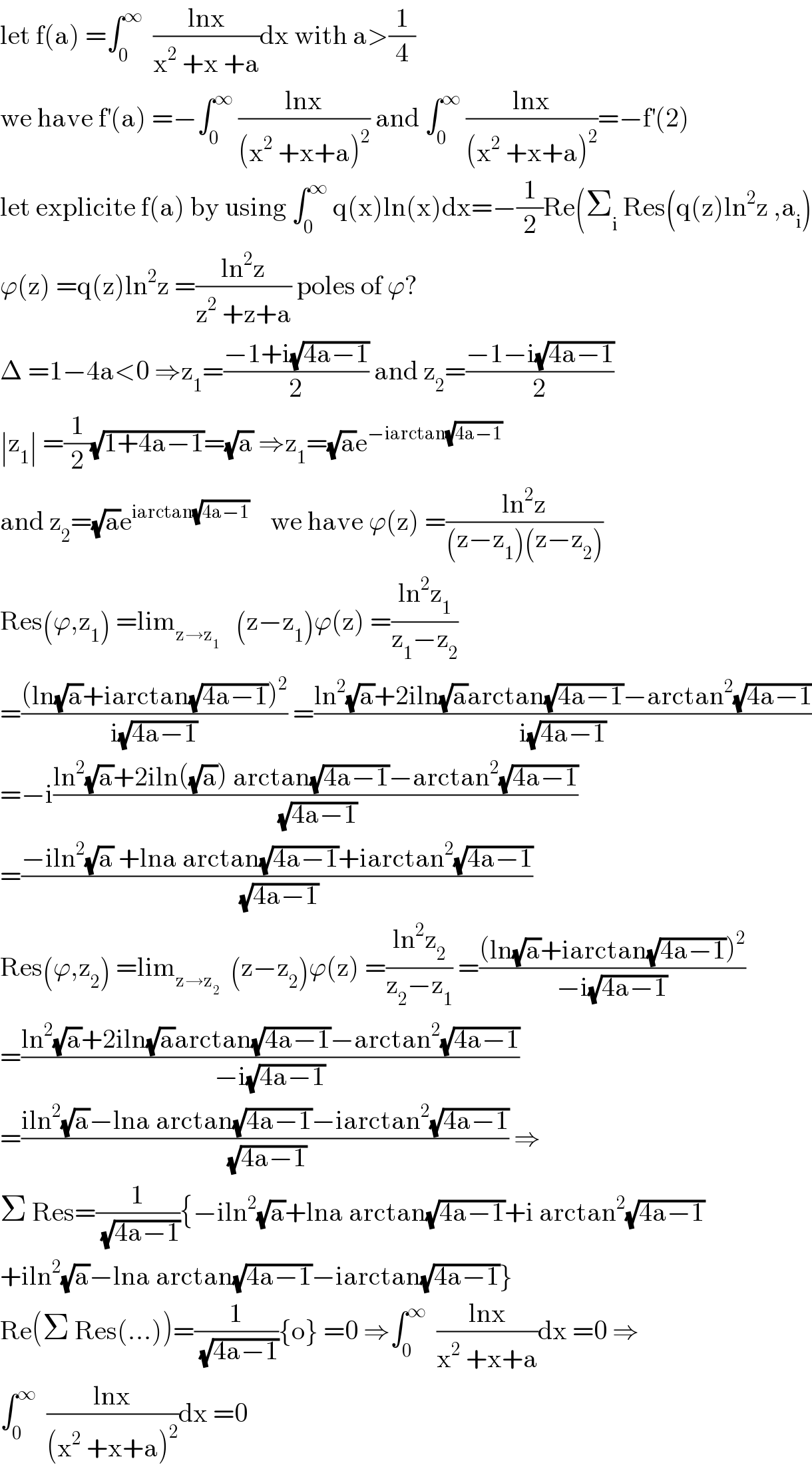
let f(a) =∫_0 ^∞ ((lnx)/(x^2 +x +a))dx with a>(1/4) we have f^′ (a) =−∫_0 ^∞ ((lnx)/((x^2 +x+a)^2 )) and ∫_0 ^∞ ((lnx)/((x^2 +x+a)^2 ))=−f^′ (2) let explicite f(a) by using ∫_0 ^∞ q(x)ln(x)dx=−(1/2)Re(Σ_i Res(q(z)ln^2 z ,a_i ) ϕ(z) =q(z)ln^2 z =((ln^2 z)/(z^2 +z+a)) poles of ϕ? Δ =1−4a<0 ⇒z_1 =((−1+i(√(4a−1)))/2) and z_2 =((−1−i(√(4a−1)))/2) ∣z_1 ∣ =(1/2)(√(1+4a−1))=(√a) ⇒z_1 =(√a)e^(−iarctan(√(4a−1))) and z_2 =(√a)e^(iarctan(√(4a−1))) we have ϕ(z) =((ln^2 z)/((z−z_1 )(z−z_2 ))) Res(ϕ,z_1 ) =lim_(z→z_1 ) (z−z_1 )ϕ(z) =((ln^2 z_1 )/(z_1 −z_2 )) =(((ln(√a)+iarctan(√(4a−1)))^2 )/(i(√(4a−1)))) =((ln^2 (√a)+2iln(√a)arctan(√(4a−1))−arctan^2 (√(4a−1)))/(i(√(4a−1)))) =−i((ln^2 (√a)+2iln((√a)) arctan(√(4a−1))−arctan^2 (√(4a−1)))/( (√(4a−1)))) =((−iln^2 (√a) +lna arctan(√(4a−1))+iarctan^2 (√(4a−1)))/( (√(4a−1)))) Res(ϕ,z_2 ) =lim_(z→z_2 ) (z−z_2 )ϕ(z) =((ln^2 z_2 )/(z_2 −z_1 )) =(((ln(√a)+iarctan(√(4a−1)))^2 )/(−i(√(4a−1)))) =((ln^2 (√a)+2iln(√a)arctan(√(4a−1))−arctan^2 (√(4a−1)))/(−i(√(4a−1)))) =((iln^2 (√a)−lna arctan(√(4a−1))−iarctan^2 (√(4a−1)))/( (√(4a−1)))) ⇒ Σ Res=(1/( (√(4a−1)))){−iln^2 (√a)+lna arctan(√(4a−1))+i arctan^2 (√(4a−1)) +iln^2 (√a)−lna arctan(√(4a−1))−iarctan(√(4a−1))} Re(Σ Res(...))=(1/( (√(4a−1)))){o} =0 ⇒∫_0 ^∞ ((lnx)/(x^2 +x+a))dx =0 ⇒ ∫_0 ^∞ ((lnx)/((x^2 +x+a)^2 ))dx =0
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{a}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{lnx}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}\:+\mathrm{a}}\mathrm{dx}\:\mathrm{with}\:\mathrm{a}>\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{f}^{'} \left(\mathrm{a}\right)\:=−\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{lnx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{a}\right)^{\mathrm{2}} }\:\mathrm{and}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{lnx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{a}\right)^{\mathrm{2}} }=−\mathrm{f}^{'} \left(\mathrm{2}\right) \\ $$$$\mathrm{let}\:\mathrm{explicite}\:\mathrm{f}\left(\mathrm{a}\right)\:\mathrm{by}\:\mathrm{using}\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{q}\left(\mathrm{x}\right)\mathrm{ln}\left(\mathrm{x}\right)\mathrm{dx}=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{Re}\left(\sum_{\mathrm{i}} \:\mathrm{Res}\left(\mathrm{q}\left(\mathrm{z}\right)\mathrm{ln}^{\mathrm{2}} \mathrm{z}\:,\mathrm{a}_{\mathrm{i}} \right)\right. \\ $$$$\varphi\left(\mathrm{z}\right)\:=\mathrm{q}\left(\mathrm{z}\right)\mathrm{ln}^{\mathrm{2}} \mathrm{z}\:=\frac{\mathrm{ln}^{\mathrm{2}} \mathrm{z}}{\mathrm{z}^{\mathrm{2}} \:+\mathrm{z}+\mathrm{a}}\:\mathrm{poles}\:\mathrm{of}\:\varphi? \\ $$$$\Delta\:=\mathrm{1}−\mathrm{4a}<\mathrm{0}\:\Rightarrow\mathrm{z}_{\mathrm{1}} =\frac{−\mathrm{1}+\mathrm{i}\sqrt{\mathrm{4a}−\mathrm{1}}}{\mathrm{2}}\:\mathrm{and}\:\mathrm{z}_{\mathrm{2}} =\frac{−\mathrm{1}−\mathrm{i}\sqrt{\mathrm{4a}−\mathrm{1}}}{\mathrm{2}} \\ $$$$\mid\mathrm{z}_{\mathrm{1}} \mid\:=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{1}+\mathrm{4a}−\mathrm{1}}=\sqrt{\mathrm{a}}\:\Rightarrow\mathrm{z}_{\mathrm{1}} =\sqrt{\mathrm{a}}\mathrm{e}^{−\mathrm{iarctan}\sqrt{\mathrm{4a}−\mathrm{1}}} \\ $$$$\mathrm{and}\:\mathrm{z}_{\mathrm{2}} =\sqrt{\mathrm{a}}\mathrm{e}^{\mathrm{iarctan}\sqrt{\mathrm{4a}−\mathrm{1}}} \:\:\:\:\mathrm{we}\:\mathrm{have}\:\varphi\left(\mathrm{z}\right)\:=\frac{\mathrm{ln}^{\mathrm{2}} \mathrm{z}}{\left(\mathrm{z}−\mathrm{z}_{\mathrm{1}} \right)\left(\mathrm{z}−\mathrm{z}_{\mathrm{2}} \right)} \\ $$$$\mathrm{Res}\left(\varphi,\mathrm{z}_{\mathrm{1}} \right)\:=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{z}_{\mathrm{1}} } \:\:\:\left(\mathrm{z}−\mathrm{z}_{\mathrm{1}} \right)\varphi\left(\mathrm{z}\right)\:=\frac{\mathrm{ln}^{\mathrm{2}} \mathrm{z}_{\mathrm{1}} }{\mathrm{z}_{\mathrm{1}} −\mathrm{z}_{\mathrm{2}} } \\ $$$$=\frac{\left(\mathrm{ln}\sqrt{\mathrm{a}}+\mathrm{iarctan}\sqrt{\mathrm{4a}−\mathrm{1}}\right)^{\mathrm{2}} }{\mathrm{i}\sqrt{\mathrm{4a}−\mathrm{1}}}\:=\frac{\mathrm{ln}^{\mathrm{2}} \sqrt{\mathrm{a}}+\mathrm{2iln}\sqrt{\mathrm{a}}\mathrm{arctan}\sqrt{\mathrm{4a}−\mathrm{1}}−\mathrm{arctan}^{\mathrm{2}} \sqrt{\mathrm{4a}−\mathrm{1}}}{\mathrm{i}\sqrt{\mathrm{4a}−\mathrm{1}}} \\ $$$$=−\mathrm{i}\frac{\mathrm{ln}^{\mathrm{2}} \sqrt{\mathrm{a}}+\mathrm{2iln}\left(\sqrt{\mathrm{a}}\right)\:\mathrm{arctan}\sqrt{\mathrm{4a}−\mathrm{1}}−\mathrm{arctan}^{\mathrm{2}} \sqrt{\mathrm{4a}−\mathrm{1}}}{\:\sqrt{\mathrm{4a}−\mathrm{1}}} \\ $$$$=\frac{−\mathrm{iln}^{\mathrm{2}} \sqrt{\mathrm{a}}\:+\mathrm{lna}\:\mathrm{arctan}\sqrt{\mathrm{4a}−\mathrm{1}}+\mathrm{iarctan}^{\mathrm{2}} \sqrt{\mathrm{4a}−\mathrm{1}}}{\:\sqrt{\mathrm{4a}−\mathrm{1}}} \\ $$$$\mathrm{Res}\left(\varphi,\mathrm{z}_{\mathrm{2}} \right)\:=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{z}_{\mathrm{2}} } \:\:\left(\mathrm{z}−\mathrm{z}_{\mathrm{2}} \right)\varphi\left(\mathrm{z}\right)\:=\frac{\mathrm{ln}^{\mathrm{2}} \mathrm{z}_{\mathrm{2}} }{\mathrm{z}_{\mathrm{2}} −\mathrm{z}_{\mathrm{1}} }\:=\frac{\left(\mathrm{ln}\sqrt{\mathrm{a}}+\mathrm{iarctan}\sqrt{\mathrm{4a}−\mathrm{1}}\right)^{\mathrm{2}} }{−\mathrm{i}\sqrt{\mathrm{4a}−\mathrm{1}}} \\ $$$$=\frac{\mathrm{ln}^{\mathrm{2}} \sqrt{\mathrm{a}}+\mathrm{2iln}\sqrt{\mathrm{a}}\mathrm{arctan}\sqrt{\mathrm{4a}−\mathrm{1}}−\mathrm{arctan}^{\mathrm{2}} \sqrt{\mathrm{4a}−\mathrm{1}}}{−\mathrm{i}\sqrt{\mathrm{4a}−\mathrm{1}}} \\ $$$$=\frac{\mathrm{iln}^{\mathrm{2}} \sqrt{\mathrm{a}}−\mathrm{lna}\:\mathrm{arctan}\sqrt{\mathrm{4a}−\mathrm{1}}−\mathrm{iarctan}^{\mathrm{2}} \sqrt{\mathrm{4a}−\mathrm{1}}}{\:\sqrt{\mathrm{4a}−\mathrm{1}}}\:\Rightarrow \\ $$$$\Sigma\:\mathrm{Res}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{4a}−\mathrm{1}}}\left\{−\mathrm{iln}^{\mathrm{2}} \sqrt{\mathrm{a}}+\mathrm{lna}\:\mathrm{arctan}\sqrt{\mathrm{4a}−\mathrm{1}}+\mathrm{i}\:\mathrm{arctan}^{\mathrm{2}} \sqrt{\mathrm{4a}−\mathrm{1}}\right. \\ $$$$\left.+\mathrm{iln}^{\mathrm{2}} \sqrt{\mathrm{a}}−\mathrm{lna}\:\mathrm{arctan}\sqrt{\mathrm{4a}−\mathrm{1}}−\mathrm{iarctan}\sqrt{\mathrm{4a}−\mathrm{1}}\right\} \\ $$$$\mathrm{Re}\left(\Sigma\:\mathrm{Res}\left(…\right)\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{4a}−\mathrm{1}}}\left\{\mathrm{o}\right\}\:=\mathrm{0}\:\Rightarrow\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{lnx}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{a}}\mathrm{dx}\:=\mathrm{0}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{lnx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{a}\right)^{\mathrm{2}} }\mathrm{dx}\:=\mathrm{0} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *