Menu Close

calculate-0-logx-x-2-x-1-dx-

Tinku Tara 0 Comments
Pin




Question Number 148570 by mathmax by abdo last updated on 29/Jul/21
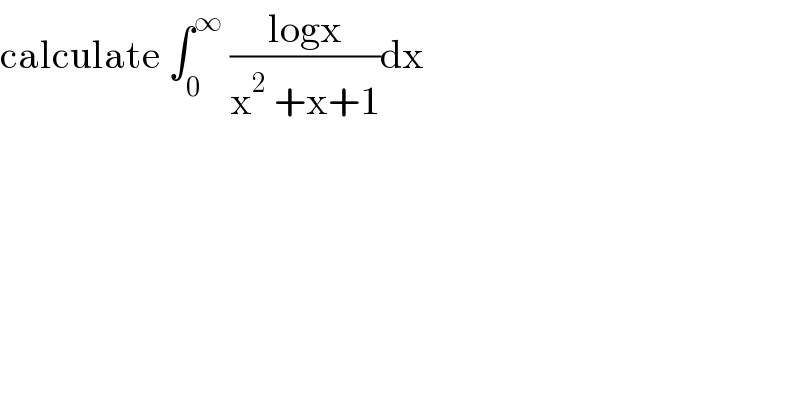
calculate ∫_0 ^∞ ((logx)/(x^2 +x+1))dx
$$\mathrm{calculate}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{logx}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{1}}\mathrm{dx} \\ $$
Answered by Ar Brandon last updated on 29/Jul/21
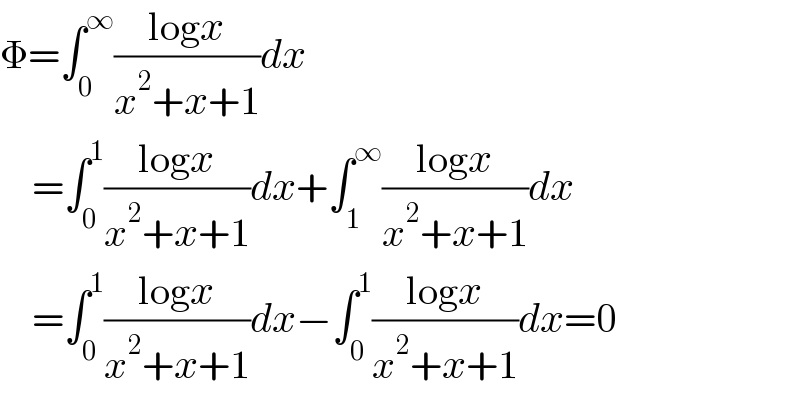
Φ=∫_0 ^∞ ((logx)/(x^2 +x+1))dx =∫_0 ^1 ((logx)/(x^2 +x+1))dx+∫_1 ^∞ ((logx)/(x^2 +x+1))dx =∫_0 ^1 ((logx)/(x^2 +x+1))dx−∫_0 ^1 ((logx)/(x^2 +x+1))dx=0
$$\Phi=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{log}{x}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{dx} \\ $$$$\:\:\:\:=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{log}{x}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{dx}+\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{log}{x}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{dx} \\ $$$$\:\:\:\:=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{log}{x}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{dx}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{log}{x}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}{dx}=\mathrm{0} \\ $$
Answered by mathmax by abdo last updated on 29/Jul/21
∫_0 ^∞ ((logx)/(x^2 +x+1))dx =−(1/2)Re(Σ Res(f(z)log^2 z ,a_i ) f(z)=(1/(z^2 +z+1)) poles of f! Δ=1−4=−3 ⇒z_1 =((−1+i(√3))/2) =e^((2iπ)/3) and z_2 =((−1−i(√3))/2) ϕ(z)=f(z)log^2 z ⇒ϕ(z)=((log^2 z)/((z−z_1 )(z−z_2 ))) Res(ϕ,e^((2iπ)/3) ) =(((((2iπ)/3))^2 )/(i(√3))) =−((4π^2 )/(9(i(√3)))) =((4iπ^2 )/(9(√3))) Res(ϕ,e^(−((2iπ)/3)) )=(((−((2iπ)/3))^2 )/(−i(√3)))=((4π^2 )/(9(i(√3))))=((−4iπ^2 )/(9(√3))) ⇒ Σ Res(ϕ..)=0 ⇒∫_0 ^∞ ((logx)/(x^2 +x+1))dx=0
$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{logx}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{1}}\mathrm{dx}\:=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{Re}\left(\Sigma\:\mathrm{Res}\left(\mathrm{f}\left(\mathrm{z}\right)\mathrm{log}^{\mathrm{2}} \mathrm{z}\:,\mathrm{a}_{\mathrm{i}} \right)\right. \\ $$$$\mathrm{f}\left(\mathrm{z}\right)=\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{2}} \:+\mathrm{z}+\mathrm{1}}\:\:\mathrm{poles}\:\mathrm{of}\:\mathrm{f}! \\ $$$$\Delta=\mathrm{1}−\mathrm{4}=−\mathrm{3}\:\Rightarrow\mathrm{z}_{\mathrm{1}} =\frac{−\mathrm{1}+\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\:=\mathrm{e}^{\frac{\mathrm{2i}\pi}{\mathrm{3}}} \:\:\mathrm{and}\:\mathrm{z}_{\mathrm{2}} =\frac{−\mathrm{1}−\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\varphi\left(\mathrm{z}\right)=\mathrm{f}\left(\mathrm{z}\right)\mathrm{log}^{\mathrm{2}} \mathrm{z}\:\Rightarrow\varphi\left(\mathrm{z}\right)=\frac{\mathrm{log}^{\mathrm{2}} \mathrm{z}}{\left(\mathrm{z}−\mathrm{z}_{\mathrm{1}} \right)\left(\mathrm{z}−\mathrm{z}_{\mathrm{2}} \right)} \\ $$$$\mathrm{Res}\left(\varphi,\mathrm{e}^{\frac{\mathrm{2i}\pi}{\mathrm{3}}} \right)\:=\frac{\left(\frac{\mathrm{2i}\pi}{\mathrm{3}}\right)^{\mathrm{2}} }{\mathrm{i}\sqrt{\mathrm{3}}}\:=−\frac{\mathrm{4}\pi^{\mathrm{2}} }{\mathrm{9}\left(\mathrm{i}\sqrt{\mathrm{3}}\right)}\:=\frac{\mathrm{4i}\pi^{\mathrm{2}} }{\mathrm{9}\sqrt{\mathrm{3}}} \\ $$$$\mathrm{Res}\left(\varphi,\mathrm{e}^{−\frac{\mathrm{2i}\pi}{\mathrm{3}}} \right)=\frac{\left(−\frac{\mathrm{2i}\pi}{\mathrm{3}}\right)^{\mathrm{2}} }{−\mathrm{i}\sqrt{\mathrm{3}}}=\frac{\mathrm{4}\pi^{\mathrm{2}} }{\mathrm{9}\left(\mathrm{i}\sqrt{\mathrm{3}}\right)}=\frac{−\mathrm{4i}\pi^{\mathrm{2}} }{\mathrm{9}\sqrt{\mathrm{3}}}\:\Rightarrow \\ $$$$\Sigma\:\mathrm{Res}\left(\varphi..\right)=\mathrm{0}\:\Rightarrow\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{logx}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{1}}\mathrm{dx}=\mathrm{0} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *