Question Number 31077 by abdo imad last updated on 02/Mar/18
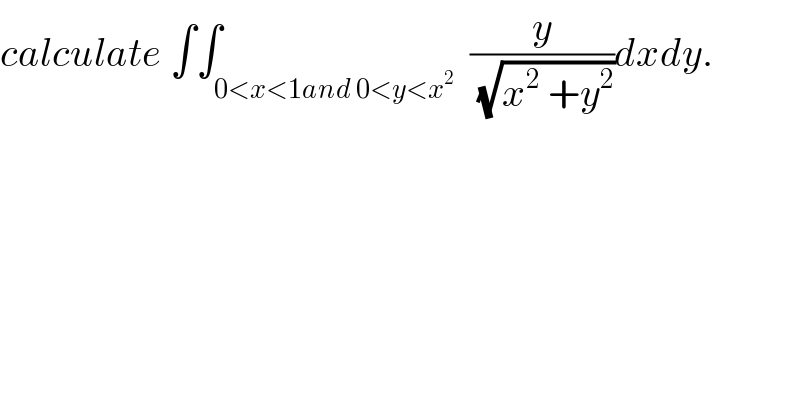
$${calculate}\:\int\int_{\mathrm{0}<{x}<\mathrm{1}{and}\:\mathrm{0}<{y}<{x}^{\mathrm{2}} } \:\frac{{y}}{\:\sqrt{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} }}{dxdy}. \\ $$
Commented by abdo imad last updated on 07/Mar/18
![I= ∫_0 ^1 ( ∫_0 ^x^2 (y/( (√(x^2 +y^2 ))))dy)dx but ∫_0 ^x^2 (y/( (√(x^2 +y^2 ))))dy= [(√(x^2 +y^2 ))^ ]_(y=0) ^(y=x^2 ) =(√(x^2 +x^4 )) −x ⇒ I= ∫_0 ^1 ((√(x^2 +x^4 )) −x)dx =∫_0 ^1 (√(x^2 +x^4 )) dx −(1/2) but ∫_0 ^1 (√(x^2 +x^4 )) dx=∫_0 ^1 x(√(1+x^2 )) dx =(1/2) ∫_0 ^1 (2x)(1+x^2 )^(1/2) dx =(1/2) [ (2/3)(1+x^2 )^(3/2) ]_0 ^1 =(1/3)( 2^(3/2) −1)=(1/3)(2(√2) −1) ⇒ I=((2(√2))/3) −(1/3) −(1/2)=((2(√2))/3) −(5/6) .](https://www.tinkutara.com/question/Q31396.png)
$${I}=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\left(\:\:\int_{\mathrm{0}} ^{{x}^{\mathrm{2}} } \:\:\frac{{y}}{\:\sqrt{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} }}{dy}\right){dx}\:\:{but} \\ $$$$\int_{\mathrm{0}} ^{{x}^{\mathrm{2}} } \:\:\frac{{y}}{\:\sqrt{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} }}{dy}=\:\left[\sqrt{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} }\:^{} \right]_{{y}=\mathrm{0}} ^{{y}={x}^{\mathrm{2}} } \:=\sqrt{{x}^{\mathrm{2}} \:+{x}^{\mathrm{4}} }\:−{x}\:\Rightarrow \\ $$$${I}=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\left(\sqrt{{x}^{\mathrm{2}} \:+{x}^{\mathrm{4}} }\:−{x}\right){dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{{x}^{\mathrm{2}} \:+{x}^{\mathrm{4}} \:}\:{dx}\:−\frac{\mathrm{1}}{\mathrm{2}}\:\:{but} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\sqrt{{x}^{\mathrm{2}} \:+{x}^{\mathrm{4}} }\:{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} {x}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{2}{x}\right)\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} {dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\left[\:\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} \right]_{\mathrm{0}} ^{\mathrm{1}} \:=\frac{\mathrm{1}}{\mathrm{3}}\left(\:\mathrm{2}^{\frac{\mathrm{3}}{\mathrm{2}}} \:−\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{2}\sqrt{\mathrm{2}}\:−\mathrm{1}\right)\:\Rightarrow \\ $$$${I}=\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}\:−\frac{\mathrm{1}}{\mathrm{3}}\:−\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}\:−\frac{\mathrm{5}}{\mathrm{6}}\:. \\ $$
