Menu Close

calculate-0-pi-2-dx-cos-2-x-3-sin-2-x-

Tinku Tara 0 Comments
Pin




Question Number 83252 by mathmax by abdo last updated on 29/Feb/20
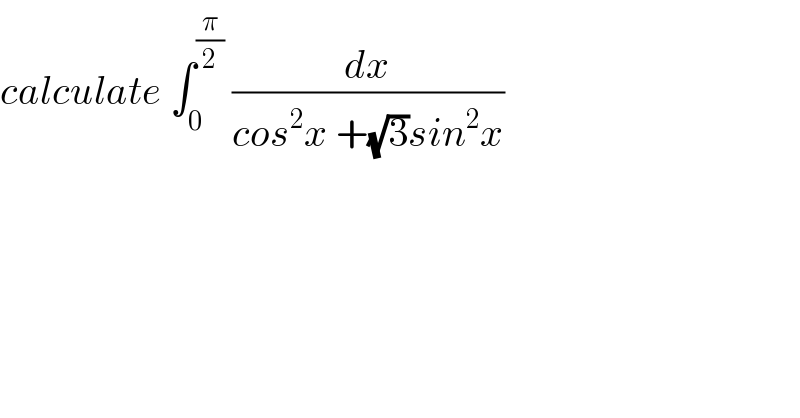
calculate ∫_0 ^(π/2) (dx/(cos^2 x +(√3)sin^2 x))
$${calculate}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{dx}}{{cos}^{\mathrm{2}} {x}\:+\sqrt{\mathrm{3}}{sin}^{\mathrm{2}} {x}} \\ $$
Commented by mathmax by abdo last updated on 29/Feb/20
I =∫_0 ^(π/2) (dx/(((1+cos(2x))/2)+(√3)((1−cos(2x))/2))) =2∫_0 ^(π/2) (dx/((1−(√3))cos(2x)+1+(√3))) =_(2x=t) 2∫_0 ^π (dt/(2{ (1−(√3))cost+1+(√3)))) =∫_0 ^π (dt/((1−(√3))cost +1+(√3))) =_(tan((t/2))=u) ∫_0 ^∞ ((2du)/((1+u^2 ){(1−(√3))×((1−u^2 )/(1+u^2 )) +1+(√3)})) =2∫_0 ^∞ (du/((1−(√3))(1−u^2 ) +(1+(√3))(1+u^2 ))) =2∫_0 ^∞ (du/(1−(√3)−(1−(√3))u^2 +(1+(√3))+(1+(√3))u^2 )) =2∫_0 ^∞ (du/(2 +(1+(√3)−1+(√3))u^2 )) =2∫_0 ^∞ (du/(2+2(√3)u^2 ))=∫_0 ^∞ (du/(1+(√3)u^2 )) =_((√(√3))u=z) ∫_0 ^∞ (dz/((^4 (√3))(1+z^2 ))) =(1/((^4 (√3))))×(π/2)
$${I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{dx}}{\frac{\mathrm{1}+{cos}\left(\mathrm{2}{x}\right)}{\mathrm{2}}+\sqrt{\mathrm{3}}\frac{\mathrm{1}−{cos}\left(\mathrm{2}{x}\right)}{\mathrm{2}}}\:=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{dx}}{\left(\mathrm{1}−\sqrt{\mathrm{3}}\right){cos}\left(\mathrm{2}{x}\right)+\mathrm{1}+\sqrt{\mathrm{3}}} \\ $$$$=_{\mathrm{2}{x}={t}} \:\:\:\:\mathrm{2}\int_{\mathrm{0}} ^{\pi} \:\:\:\frac{{dt}}{\mathrm{2}\left\{\:\left(\mathrm{1}−\sqrt{\mathrm{3}}\right){cost}+\mathrm{1}+\sqrt{\mathrm{3}}\right)}\:=\int_{\mathrm{0}} ^{\pi} \:\frac{{dt}}{\left(\mathrm{1}−\sqrt{\mathrm{3}}\right){cost}\:+\mathrm{1}+\sqrt{\mathrm{3}}} \\ $$$$=_{{tan}\left(\frac{{t}}{\mathrm{2}}\right)={u}} \:\:\:\:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{\mathrm{2}{du}}{\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\left\{\left(\mathrm{1}−\sqrt{\mathrm{3}}\right)×\frac{\mathrm{1}−{u}^{\mathrm{2}} }{\mathrm{1}+{u}^{\mathrm{2}} }\:+\mathrm{1}+\sqrt{\mathrm{3}}\right\}} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{du}}{\left(\mathrm{1}−\sqrt{\mathrm{3}}\right)\left(\mathrm{1}−{u}^{\mathrm{2}} \right)\:+\left(\mathrm{1}+\sqrt{\mathrm{3}}\right)\left(\mathrm{1}+{u}^{\mathrm{2}} \right)} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{du}}{\mathrm{1}−\sqrt{\mathrm{3}}−\left(\mathrm{1}−\sqrt{\mathrm{3}}\right){u}^{\mathrm{2}} \:+\left(\mathrm{1}+\sqrt{\mathrm{3}}\right)+\left(\mathrm{1}+\sqrt{\mathrm{3}}\right){u}^{\mathrm{2}} } \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\frac{{du}}{\mathrm{2}\:+\left(\mathrm{1}+\sqrt{\mathrm{3}}−\mathrm{1}+\sqrt{\mathrm{3}}\right){u}^{\mathrm{2}} }\:=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\frac{{du}}{\mathrm{2}+\mathrm{2}\sqrt{\mathrm{3}}{u}^{\mathrm{2}} }=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{du}}{\mathrm{1}+\sqrt{\mathrm{3}}{u}^{\mathrm{2}} } \\ $$$$=_{\sqrt{\sqrt{\mathrm{3}}}{u}={z}} \:\:\:\:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\:\frac{{dz}}{\left(^{\mathrm{4}} \sqrt{\mathrm{3}}\right)\left(\mathrm{1}+{z}^{\mathrm{2}} \right)}\:=\frac{\mathrm{1}}{\left(^{\mathrm{4}} \sqrt{\mathrm{3}}\right)}×\frac{\pi}{\mathrm{2}} \\ $$
Answered by MJS last updated on 29/Feb/20
∫(dx/(cos^2 x +(√3)sin^2 x))= [t=tan x → dx=(dt/(t^2 +1))] =∫(dt/( (√3)t^2 +1))=(((27))^(1/4) /3)arctan (3)^(1/4) t = =(((27))^(1/4) /3)arctan ((3)^(1/4) tan x) +C ∫_0 ^(π/2) (dx/(cos^2 x +(√3)sin^2 x))=(((27))^(1/4) /6)π
$$\int\frac{{dx}}{\mathrm{cos}^{\mathrm{2}} \:{x}\:+\sqrt{\mathrm{3}}\mathrm{sin}^{\mathrm{2}} \:{x}}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{tan}\:{x}\:\rightarrow\:{dx}=\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}\right] \\ $$$$=\int\frac{{dt}}{\:\sqrt{\mathrm{3}}{t}^{\mathrm{2}} +\mathrm{1}}=\frac{\sqrt[{\mathrm{4}}]{\mathrm{27}}}{\mathrm{3}}\mathrm{arctan}\:\sqrt[{\mathrm{4}}]{\mathrm{3}}{t}\:= \\ $$$$=\frac{\sqrt[{\mathrm{4}}]{\mathrm{27}}}{\mathrm{3}}\mathrm{arctan}\:\left(\sqrt[{\mathrm{4}}]{\mathrm{3}}\mathrm{tan}\:{x}\right)\:+{C} \\ $$$$\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\frac{{dx}}{\mathrm{cos}^{\mathrm{2}} \:{x}\:+\sqrt{\mathrm{3}}\mathrm{sin}^{\mathrm{2}} \:{x}}=\frac{\sqrt[{\mathrm{4}}]{\mathrm{27}}}{\mathrm{6}}\pi \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *