Menu Close

calculate-0-pi-2-dx-cos-4-x-sin-4-x-

Tinku Tara 0 Comments
Pin




Question Number 34283 by math khazana by abdo last updated on 03/May/18
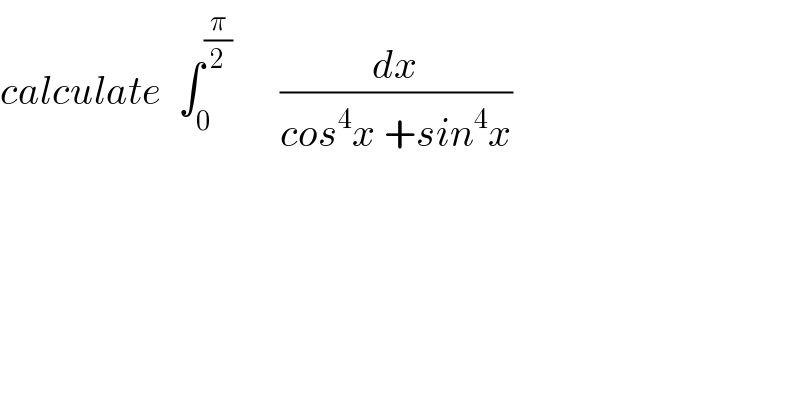
calculate ∫_0 ^(π/2) (dx/(cos^4 x +sin^4 x))
$${calculate}\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\:\:\:\frac{{dx}}{{cos}^{\mathrm{4}} {x}\:+{sin}^{\mathrm{4}} {x}} \\ $$
Commented by math khazana by abdo last updated on 08/May/18
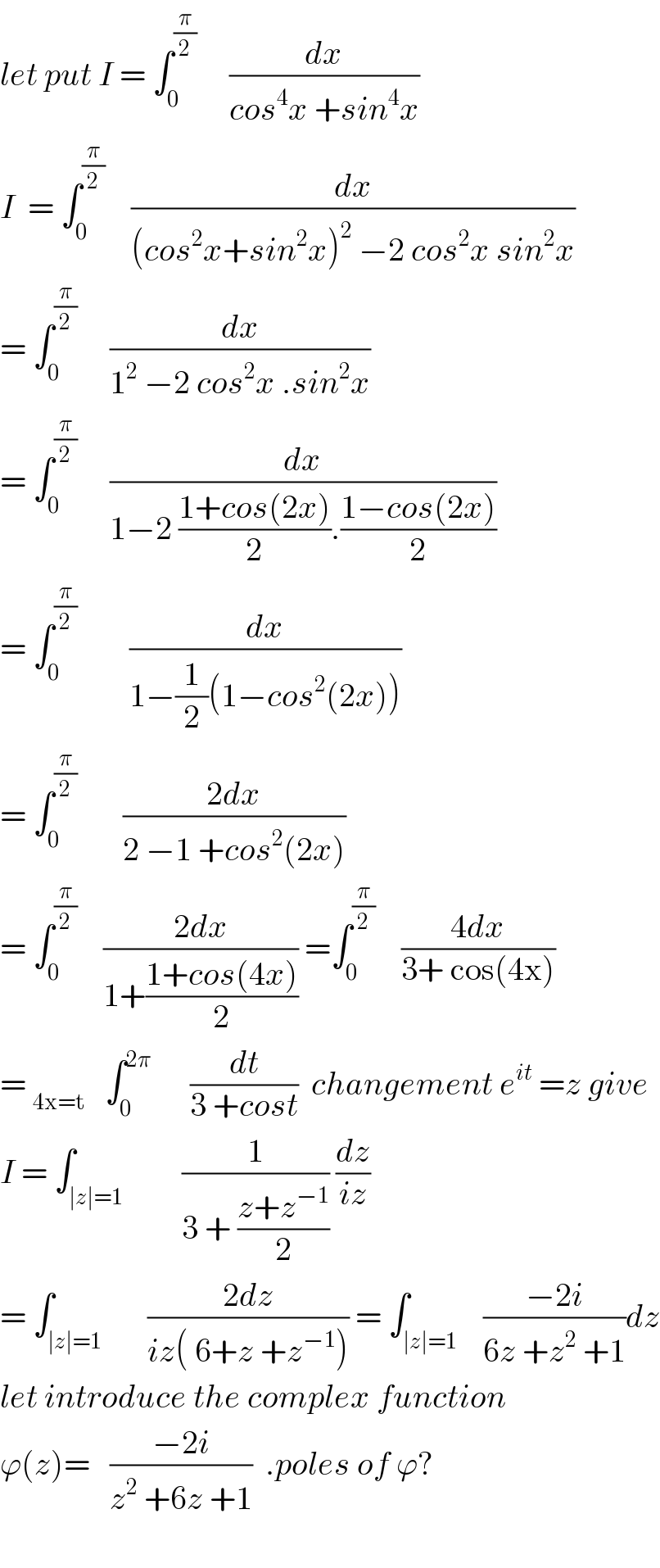
let put I = ∫_0 ^(π/2) (dx/(cos^4 x +sin^4 x)) I = ∫_0 ^(π/2) (dx/((cos^2 x+sin^2 x)^2 −2 cos^2 x sin^2 x)) = ∫_0 ^(π/2) (dx/(1^2 −2 cos^2 x .sin^2 x)) = ∫_0 ^(π/2) (dx/(1−2 ((1+cos(2x))/2).((1−cos(2x))/2))) = ∫_0 ^(π/2) (dx/(1−(1/2)(1−cos^2 (2x)))) = ∫_0 ^(π/2) ((2dx)/(2 −1 +cos^2 (2x))) = ∫_0 ^(π/2) ((2dx)/(1+((1+cos(4x))/2))) =∫_0 ^(π/2) ((4dx)/(3+ cos(4x))) = _(4x=t) ∫_0 ^(2π) (dt/(3 +cost)) changement e^(it) =z give I = ∫_(∣z∣=1) (1/(3 + ((z+z^(−1) )/2))) (dz/(iz)) = ∫_(∣z∣=1) ((2dz)/(iz( 6+z +z^(−1) ))) = ∫_(∣z∣=1) ((−2i)/(6z +z^2 +1))dz let introduce the complex function ϕ(z)= ((−2i)/(z^2 +6z +1)) .poles of ϕ?
$${let}\:{put}\:{I}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\:\:\frac{{dx}}{{cos}^{\mathrm{4}} {x}\:+{sin}^{\mathrm{4}} {x}} \\ $$$${I}\:\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\:\frac{{dx}}{\left({cos}^{\mathrm{2}} {x}+{sin}^{\mathrm{2}} {x}\right)^{\mathrm{2}} \:−\mathrm{2}\:{cos}^{\mathrm{2}} {x}\:{sin}^{\mathrm{2}} {x}} \\ $$$$=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\:\:\frac{{dx}}{\mathrm{1}^{\mathrm{2}} \:−\mathrm{2}\:{cos}^{\mathrm{2}} {x}\:.{sin}^{\mathrm{2}} {x}} \\ $$$$=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\:\:\frac{{dx}}{\mathrm{1}−\mathrm{2}\:\frac{\mathrm{1}+{cos}\left(\mathrm{2}{x}\right)}{\mathrm{2}}.\frac{\mathrm{1}−{cos}\left(\mathrm{2}{x}\right)}{\mathrm{2}}} \\ $$$$=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\:\:\:\:\:\frac{{dx}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−{cos}^{\mathrm{2}} \left(\mathrm{2}{x}\right)\right)} \\ $$$$=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\:\:\:\:\frac{\mathrm{2}{dx}}{\mathrm{2}\:−\mathrm{1}\:+{cos}^{\mathrm{2}} \left(\mathrm{2}{x}\right)} \\ $$$$=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\:\frac{\mathrm{2}{dx}}{\mathrm{1}+\frac{\mathrm{1}+{cos}\left(\mathrm{4}{x}\right)}{\mathrm{2}}}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\:\frac{\mathrm{4}{dx}}{\mathrm{3}+\:\mathrm{cos}\left(\mathrm{4x}\right)} \\ $$$$=\:_{\mathrm{4x}=\mathrm{t}} \:\:\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\:\:\:\:\frac{{dt}}{\mathrm{3}\:+{cost}}\:\:{changement}\:{e}^{{it}} \:={z}\:{give} \\ $$$${I}\:=\:\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{3}\:+\:\frac{{z}+{z}^{−\mathrm{1}} }{\mathrm{2}}}\:\frac{{dz}}{{iz}} \\ $$$$=\:\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\:\:\:\frac{\mathrm{2}{dz}}{{iz}\left(\:\mathrm{6}+{z}\:+{z}^{−\mathrm{1}} \right)}\:=\:\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\frac{−\mathrm{2}{i}}{\mathrm{6}{z}\:+{z}^{\mathrm{2}} \:+\mathrm{1}}{dz} \\ $$$${let}\:{introduce}\:{the}\:{complex}\:{function} \\ $$$$\varphi\left({z}\right)=\:\:\:\frac{−\mathrm{2}{i}}{{z}^{\mathrm{2}} \:+\mathrm{6}{z}\:+\mathrm{1}}\:\:.{poles}\:{of}\:\varphi? \\ $$$$ \\ $$
Commented by math khazana by abdo last updated on 08/May/18
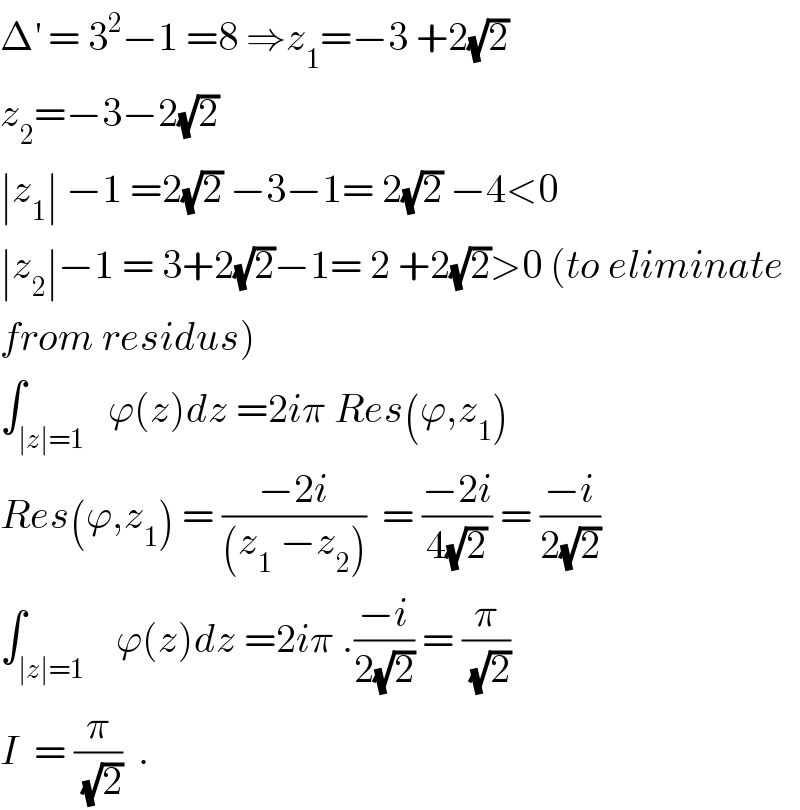
Δ^′ = 3^2 −1 =8 ⇒z_1 =−3 +2(√2) z_2 =−3−2(√2) ∣z_1 ∣ −1 =2(√2) −3−1= 2(√2) −4<0 ∣z_2 ∣−1 = 3+2(√2)−1= 2 +2(√2)>0 (to eliminate from residus) ∫_(∣z∣=1) ϕ(z)dz =2iπ Res(ϕ,z_1 ) Res(ϕ,z_1 ) = ((−2i)/((z_1 −z_2 ))) = ((−2i)/(4(√2))) = ((−i)/(2(√2))) ∫_(∣z∣=1) ϕ(z)dz =2iπ .((−i)/(2(√2))) = (π/( (√2))) I = (π/( (√2))) .
$$\Delta^{'} \:=\:\mathrm{3}^{\mathrm{2}} −\mathrm{1}\:=\mathrm{8}\:\Rightarrow{z}_{\mathrm{1}} =−\mathrm{3}\:+\mathrm{2}\sqrt{\mathrm{2}} \\ $$$${z}_{\mathrm{2}} =−\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}} \\ $$$$\mid{z}_{\mathrm{1}} \mid\:−\mathrm{1}\:=\mathrm{2}\sqrt{\mathrm{2}}\:−\mathrm{3}−\mathrm{1}=\:\mathrm{2}\sqrt{\mathrm{2}}\:−\mathrm{4}<\mathrm{0} \\ $$$$\mid{z}_{\mathrm{2}} \mid−\mathrm{1}\:=\:\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{1}=\:\mathrm{2}\:+\mathrm{2}\sqrt{\mathrm{2}}>\mathrm{0}\:\left({to}\:{eliminate}\right. \\ $$$$\left.{from}\:{residus}\right) \\ $$$$\int_{\mid{z}\mid=\mathrm{1}} \:\:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:{Res}\left(\varphi,{z}_{\mathrm{1}} \right) \\ $$$${Res}\left(\varphi,{z}_{\mathrm{1}} \right)\:=\:\frac{−\mathrm{2}{i}}{\left({z}_{\mathrm{1}} \:−{z}_{\mathrm{2}} \right)}\:\:=\:\frac{−\mathrm{2}{i}}{\mathrm{4}\sqrt{\mathrm{2}}}\:=\:\frac{−{i}}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$$\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:.\frac{−{i}}{\mathrm{2}\sqrt{\mathrm{2}}}\:=\:\frac{\pi}{\:\sqrt{\mathrm{2}}} \\ $$$${I}\:\:=\:\frac{\pi}{\:\sqrt{\mathrm{2}}}\:\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *