Question Number 120316 by Bird last updated on 30/Oct/20
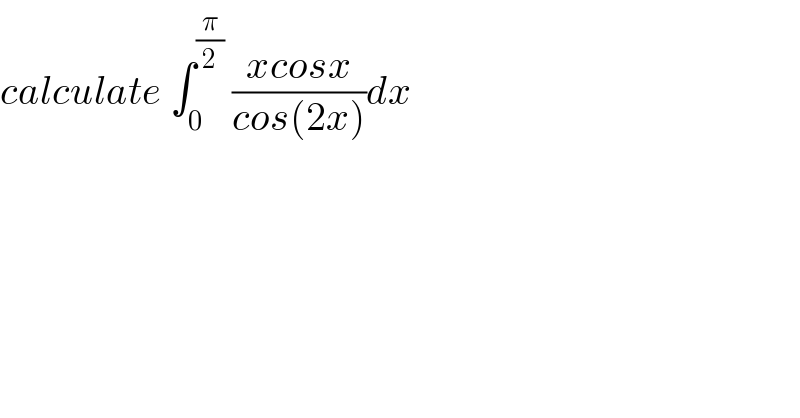
$${calculate}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{xcosx}}{{cos}\left(\mathrm{2}{x}\right)}{dx} \\ $$
Answered by mathmax by abdo last updated on 30/Oct/20
![let I=∫_0 ^(π/2) (x/(cosx+sinx))dx we have proved that I=(π/(4(√2)))ln((((√2)+1)/( (√2)−1))) changement x =t−(π/2) give I =−∫_0 ^(π/2) ((t−(π/2))/(sint−cost))dt =(π/2)∫_0 ^(π/2) (dt/(sint−cost))−∫_0 ^(π/2) (t/(sint−cost)) =∫_0 ^(π/2) (x/(cosx−sinx))dx +(π/2)∫_0 ^(π/2) (dx/(sinx−cosx)) ⇒ 2I =∫_0 ^(π/2) x((1/(cosx+sinx))+(1/(cosx−sinx)))dx+(π/2)∫_0 ^(π/2) (dx/(sinx−cosx)) =∫_0 ^(π/2) ((x(2cosx))/(cos^2 x−sin^2 x))dx+(π/2)∫_0 ^(π/2) (dx/(sinx−cosx)) ⇒2 ∫_0 ^(π/2) ((xcosx)/(cos(2x)))dx =2I−(π/2)∫_0 ^(π/2) (dx/(sinx−cosx)) ⇒ ∫_0 ^(π/2) ((xcosx)/(cos(2x)))dx =I−(π/4)∫_0 ^(π/2) (dx/(sinx−cosx)) we have ∫_0 ^(π/2) (dx/(sinx−cosx)) =_(tan((x/2))=t) ∫_0 ^1 ((2dt)/((1+t^2 )(((2t)/(1+t^2 ))−((1−t^2 )/(1+t^2 ))))) =∫_0 ^1 ((2dt)/(2t−1+t^2 )) =2 ∫_0 ^1 (dt/(t^2 +2t−1)) =2∫_0 ^1 (dt/((t+1)^2 −2)) =2∫_0 ^1 (dt/((t+1−(√2))(t+1+(√2)))) =(2/(2(√2)))∫_0 ^1 ((1/(t+1−(√2)))−(1/(t+1+(√2)))) =(1/( (√2)))[ln∣((t+1−(√2))/(t+1+(√2)))∣]_0 ^1 =(1/( (√2)))ln∣((2−(√2))/(2+(√2)))∣−ln∣((1−(√2))/(1+(√2)))∣ =(1/( (√2)))ln(((2−(√2))/(2+(√2))))−ln((((√2)−1)/( (√2)+1))) ⇒ ∫_0 ^(π/2) ((xcosx)/(cos(2x)))dx =(π/(4(√2)))ln((((√2)+1)/( (√2)−1)))−(π/(4(√2)))ln(((2−(√2))/(2+(√2))))+(π/4)ln((((√2)−1)/( (√2)+1))) =(π/4)((1/( (√2)))−1)ln((((√2)+1)/( (√2)−1)))−(π/(4(√2)))ln(((2−(√2))/(2+(√2))))](https://www.tinkutara.com/question/Q120369.png)
$$\mathrm{let}\:\mathrm{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{x}}{\mathrm{cosx}+\mathrm{sinx}}\mathrm{dx}\:\mathrm{we}\:\mathrm{have}\:\mathrm{proved}\:\mathrm{that}\:\mathrm{I}=\frac{\pi}{\mathrm{4}\sqrt{\mathrm{2}}}\mathrm{ln}\left(\frac{\sqrt{\mathrm{2}}+\mathrm{1}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}\right) \\ $$$$\mathrm{changement}\:\mathrm{x}\:=\mathrm{t}−\frac{\pi}{\mathrm{2}}\:\mathrm{give} \\ $$$$\mathrm{I}\:=−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{t}−\frac{\pi}{\mathrm{2}}}{\mathrm{sint}−\mathrm{cost}}\mathrm{dt}\:=\frac{\pi}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{dt}}{\mathrm{sint}−\mathrm{cost}}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{t}}{\mathrm{sint}−\mathrm{cost}} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{\mathrm{x}}{\mathrm{cosx}−\mathrm{sinx}}\mathrm{dx}\:+\frac{\pi}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{dx}}{\mathrm{sinx}−\mathrm{cosx}}\:\Rightarrow \\ $$$$\mathrm{2I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{x}\left(\frac{\mathrm{1}}{\mathrm{cosx}+\mathrm{sinx}}+\frac{\mathrm{1}}{\mathrm{cosx}−\mathrm{sinx}}\right)\mathrm{dx}+\frac{\pi}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{dx}}{\mathrm{sinx}−\mathrm{cosx}} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{x}\left(\mathrm{2cosx}\right)}{\mathrm{cos}^{\mathrm{2}} \mathrm{x}−\mathrm{sin}^{\mathrm{2}} \mathrm{x}}\mathrm{dx}+\frac{\pi}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{dx}}{\mathrm{sinx}−\mathrm{cosx}} \\ $$$$\Rightarrow\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{xcosx}}{\mathrm{cos}\left(\mathrm{2x}\right)}\mathrm{dx}\:=\mathrm{2I}−\frac{\pi}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{dx}}{\mathrm{sinx}−\mathrm{cosx}}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{xcosx}}{\mathrm{cos}\left(\mathrm{2x}\right)}\mathrm{dx}\:=\mathrm{I}−\frac{\pi}{\mathrm{4}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{dx}}{\mathrm{sinx}−\mathrm{cosx}}\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{dx}}{\mathrm{sinx}−\mathrm{cosx}}\:=_{\mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)=\mathrm{t}} \:\:\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{2dt}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\left(\frac{\mathrm{2t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }−\frac{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\right)} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{2dt}}{\mathrm{2t}−\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} +\mathrm{2t}−\mathrm{1}}\:=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dt}}{\left(\mathrm{t}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dt}}{\left(\mathrm{t}+\mathrm{1}−\sqrt{\mathrm{2}}\right)\left(\mathrm{t}+\mathrm{1}+\sqrt{\mathrm{2}}\right)}\:=\frac{\mathrm{2}}{\mathrm{2}\sqrt{\mathrm{2}}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\left(\frac{\mathrm{1}}{\mathrm{t}+\mathrm{1}−\sqrt{\mathrm{2}}}−\frac{\mathrm{1}}{\mathrm{t}+\mathrm{1}+\sqrt{\mathrm{2}}}\right) \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left[\mathrm{ln}\mid\frac{\mathrm{t}+\mathrm{1}−\sqrt{\mathrm{2}}}{\mathrm{t}+\mathrm{1}+\sqrt{\mathrm{2}}}\mid\right]_{\mathrm{0}} ^{\mathrm{1}} \:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{ln}\mid\frac{\mathrm{2}−\sqrt{\mathrm{2}}}{\mathrm{2}+\sqrt{\mathrm{2}}}\mid−\mathrm{ln}\mid\frac{\mathrm{1}−\sqrt{\mathrm{2}}}{\mathrm{1}+\sqrt{\mathrm{2}}}\mid \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{ln}\left(\frac{\mathrm{2}−\sqrt{\mathrm{2}}}{\mathrm{2}+\sqrt{\mathrm{2}}}\right)−\mathrm{ln}\left(\frac{\sqrt{\mathrm{2}}−\mathrm{1}}{\:\sqrt{\mathrm{2}}+\mathrm{1}}\right)\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{xcosx}}{\mathrm{cos}\left(\mathrm{2x}\right)}\mathrm{dx}\:=\frac{\pi}{\mathrm{4}\sqrt{\mathrm{2}}}\mathrm{ln}\left(\frac{\sqrt{\mathrm{2}}+\mathrm{1}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}\right)−\frac{\pi}{\mathrm{4}\sqrt{\mathrm{2}}}\mathrm{ln}\left(\frac{\mathrm{2}−\sqrt{\mathrm{2}}}{\mathrm{2}+\sqrt{\mathrm{2}}}\right)+\frac{\pi}{\mathrm{4}}\mathrm{ln}\left(\frac{\sqrt{\mathrm{2}}−\mathrm{1}}{\:\sqrt{\mathrm{2}}+\mathrm{1}}\right) \\ $$$$=\frac{\pi}{\mathrm{4}}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}−\mathrm{1}\right)\mathrm{ln}\left(\frac{\sqrt{\mathrm{2}}+\mathrm{1}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}\right)−\frac{\pi}{\mathrm{4}\sqrt{\mathrm{2}}}\mathrm{ln}\left(\frac{\mathrm{2}−\sqrt{\mathrm{2}}}{\mathrm{2}+\sqrt{\mathrm{2}}}\right) \\ $$
