Question Number 39383 by maxmathsup by imad last updated on 05/Jul/18
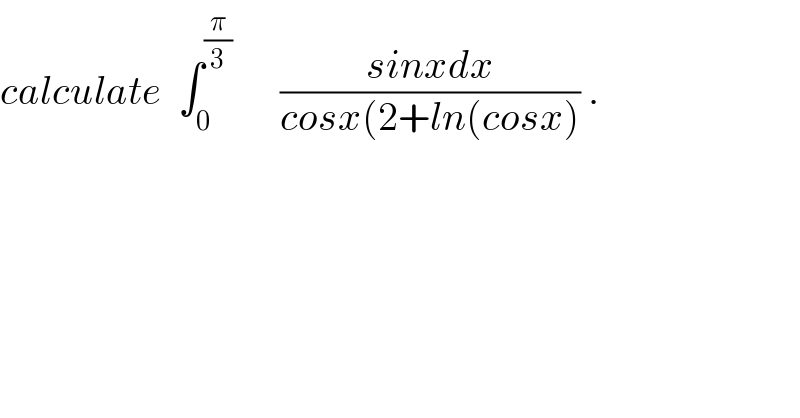
$${calculate}\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{3}}} \:\:\:\:\:\:\frac{{sinxdx}}{{cosx}\left(\mathrm{2}+{ln}\left({cosx}\right)\right.}\:. \\ $$
Commented by math khazana by abdo last updated on 06/Jul/18
![chanvement cosx =t give I = ∫_1 ^(1/2) ((√(1−t^2 ))/(t(2+ln(t)))) ((−dt)/( (√(1−t^2 )))) = ∫_(1/2) ^1 (dt/(t(2 +ln(t)))) then we do the chang. ln(t)=u ⇒I = ∫_(−ln(2)) ^0 ((e^u du)/(e^u (2 +u))) = ∫_(−ln(2)) ^0 (du/(2+u)) =[ln∣2+u∣]_(−ln(2)) ^0 =ln(2) −ln(2−ln(2)) .](https://www.tinkutara.com/question/Q39467.png)
$${chanvement}\:\:{cosx}\:={t}\:{give} \\ $$$${I}\:\:=\:\int_{\mathrm{1}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:\:\:\:\:\frac{\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}{{t}\left(\mathrm{2}+{ln}\left({t}\right)\right)}\:\frac{−{dt}}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }} \\ $$$$=\:\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{\mathrm{1}} \:\:\:\:\:\:\frac{{dt}}{{t}\left(\mathrm{2}\:+{ln}\left({t}\right)\right)}\:{then}\:{we}\:{do}\:{the}\:{chang}. \\ $$$${ln}\left({t}\right)={u}\:\Rightarrow{I}\:=\:\int_{−{ln}\left(\mathrm{2}\right)} ^{\mathrm{0}} \:\frac{{e}^{{u}} \:{du}}{{e}^{{u}} \left(\mathrm{2}\:+{u}\right)} \\ $$$$=\:\int_{−{ln}\left(\mathrm{2}\right)} ^{\mathrm{0}} \:\:\:\:\frac{{du}}{\mathrm{2}+{u}}\:=\left[{ln}\mid\mathrm{2}+{u}\mid\right]_{−{ln}\left(\mathrm{2}\right)} ^{\mathrm{0}} \\ $$$$={ln}\left(\mathrm{2}\right)\:−{ln}\left(\mathrm{2}−{ln}\left(\mathrm{2}\right)\right)\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 06/Jul/18
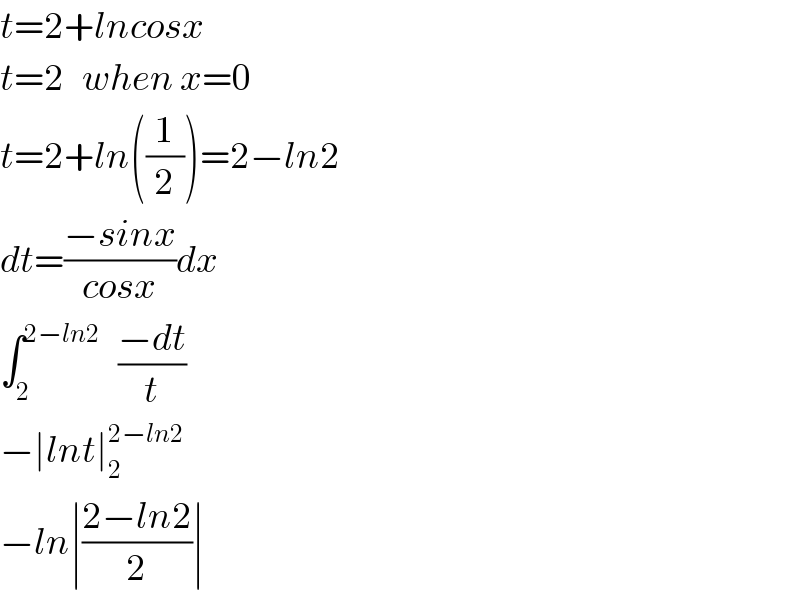
$${t}=\mathrm{2}+{lncosx} \\ $$$${t}=\mathrm{2}\:\:\:{when}\:{x}=\mathrm{0} \\ $$$${t}=\mathrm{2}+{ln}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{2}−{ln}\mathrm{2} \\ $$$${dt}=\frac{−{sinx}}{{cosx}}{dx} \\ $$$$\int_{\mathrm{2}} ^{\mathrm{2}−{ln}\mathrm{2}} \:\:\:\frac{−{dt}}{{t}} \\ $$$$−\mid{lnt}\mid_{\mathrm{2}} ^{\mathrm{2}−{ln}\mathrm{2}} \\ $$$$−{ln}\mid\frac{\mathrm{2}−{ln}\mathrm{2}}{\mathrm{2}}\mid \\ $$
Commented by math khazana by abdo last updated on 06/Jul/18
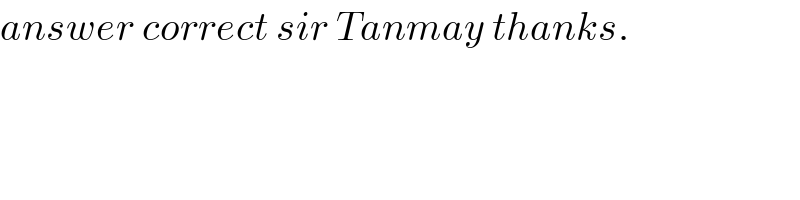
$${answer}\:{correct}\:{sir}\:{Tanmay}\:{thanks}. \\ $$
