Menu Close

calculate-0-pi-4-dx-cos-3-x-sin-3-x-

Tinku Tara 0 Comments
Pin




Question Number 34219 by abdo imad last updated on 03/May/18
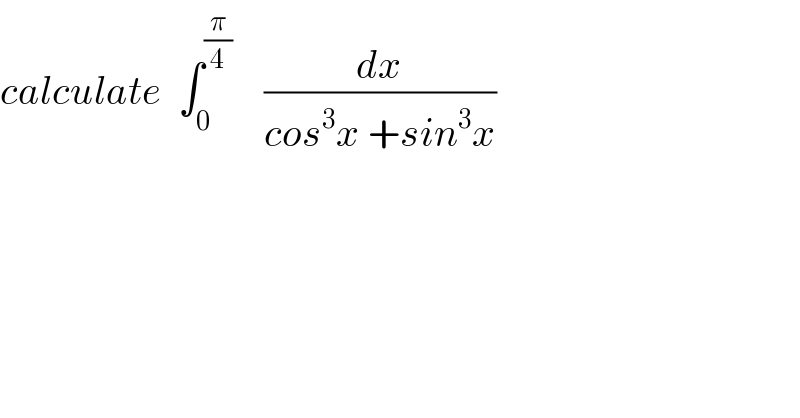
calculate ∫_0 ^(π/4) (dx/(cos^3 x +sin^3 x))
$${calculate}\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\:\frac{{dx}}{{cos}^{\mathrm{3}} {x}\:+{sin}^{\mathrm{3}} {x}} \\ $$
Commented by abdo imad last updated on 31/May/18
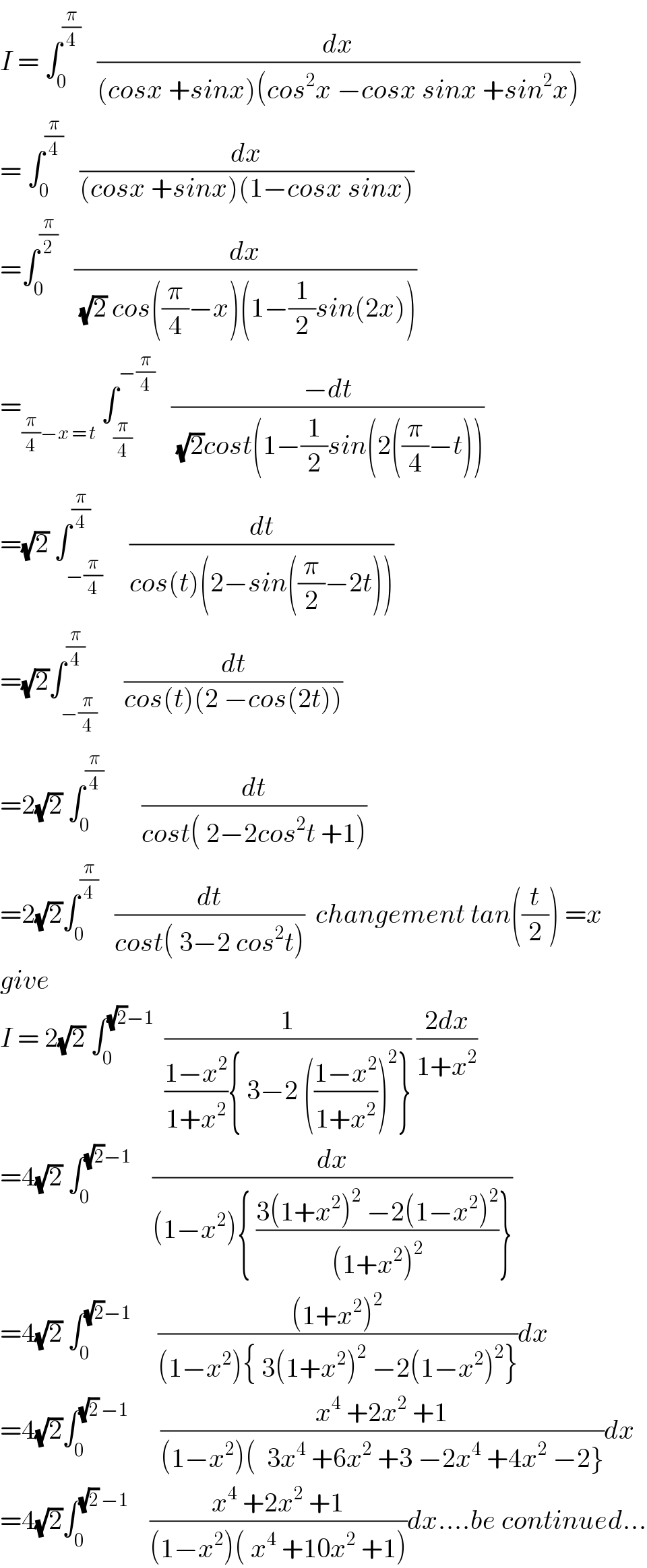
I = ∫_0 ^(π/4) (dx/((cosx +sinx)(cos^2 x −cosx sinx +sin^2 x))) = ∫_0 ^(π/4) (dx/((cosx +sinx)(1−cosx sinx))) =∫_0 ^(π/2) (dx/( (√2) cos((π/4)−x)(1−(1/2)sin(2x)))) =_((π/4)−x = t) ∫_(π/4) ^(−(π/4)) ((−dt)/( (√2)cost(1−(1/2)sin(2((π/4)−t)))) =(√2) ∫_(−(π/4)) ^(π/4) (dt/(cos(t)(2−sin((π/2)−2t)))) =(√2)∫_(−(π/4)) ^(π/4) (dt/(cos(t)(2 −cos(2t)))) =2(√2) ∫_0 ^(π/4) (dt/(cost( 2−2cos^2 t +1))) =2(√2)∫_0 ^(π/4) (dt/(cost( 3−2 cos^2 t))) changement tan((t/2)) =x give I = 2(√2) ∫_0 ^((√2)−1) (1/(((1−x^2 )/(1+x^2 )){ 3−2 (((1−x^2 )/(1+x^2 )))^2 })) ((2dx)/(1+x^2 )) =4(√2) ∫_0 ^((√2)−1) (dx/((1−x^2 ){ ((3(1+x^2 )^2 −2(1−x^2 )^2 )/((1+x^2 )^2 ))})) =4(√2) ∫_0 ^((√2)−1) (((1+x^2 )^2 )/((1−x^2 ){ 3(1+x^2 )^2 −2(1−x^2 )^2 }))dx =4(√2)∫_0 ^((√2) −1) ((x^4 +2x^2 +1)/((1−x^2 )( 3x^4 +6x^2 +3 −2x^4 +4x^2 −2}))dx =4(√2)∫_0 ^((√2) −1) ((x^4 +2x^2 +1)/((1−x^2 )( x^4 +10x^2 +1)))dx....be continued...
$${I}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\frac{{dx}}{\left({cosx}\:+{sinx}\right)\left({cos}^{\mathrm{2}} {x}\:−{cosx}\:{sinx}\:+{sin}^{\mathrm{2}} {x}\right)} \\ $$$$=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\frac{{dx}}{\left({cosx}\:+{sinx}\right)\left(\mathrm{1}−{cosx}\:{sinx}\right)} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\frac{{dx}}{\:\sqrt{\mathrm{2}}\:{cos}\left(\frac{\pi}{\mathrm{4}}−{x}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}{sin}\left(\mathrm{2}{x}\right)\right)} \\ $$$$=_{\frac{\pi}{\mathrm{4}}−{x}\:=\:{t}} \:\int_{\frac{\pi}{\mathrm{4}}} ^{−\frac{\pi}{\mathrm{4}}} \:\:\:\frac{−{dt}}{\:\sqrt{\mathrm{2}}{cost}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}{sin}\left(\mathrm{2}\left(\frac{\pi}{\mathrm{4}}−{t}\right)\right)\right.} \\ $$$$=\sqrt{\mathrm{2}}\:\int_{−\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\:\frac{{dt}}{{cos}\left({t}\right)\left(\mathrm{2}−{sin}\left(\frac{\pi}{\mathrm{2}}−\mathrm{2}{t}\right)\right)} \\ $$$$=\sqrt{\mathrm{2}}\int_{−\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\:\frac{{dt}}{{cos}\left({t}\right)\left(\mathrm{2}\:−{cos}\left(\mathrm{2}{t}\right)\right)} \\ $$$$=\mathrm{2}\sqrt{\mathrm{2}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\:\:\:\:\frac{{dt}}{{cost}\left(\:\mathrm{2}−\mathrm{2}{cos}^{\mathrm{2}} {t}\:+\mathrm{1}\right)} \\ $$$$=\mathrm{2}\sqrt{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\frac{{dt}}{{cost}\left(\:\mathrm{3}−\mathrm{2}\:{cos}^{\mathrm{2}} {t}\right)}\:\:{changement}\:{tan}\left(\frac{{t}}{\mathrm{2}}\right)\:={x} \\ $$$${give}\: \\ $$$${I}\:=\:\mathrm{2}\sqrt{\mathrm{2}}\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\:\frac{\mathrm{1}}{\frac{\mathrm{1}−{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }\left\{\:\mathrm{3}−\mathrm{2}\:\left(\frac{\mathrm{1}−{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }\right)^{\mathrm{2}} \right\}}\:\frac{\mathrm{2}{dx}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$$=\mathrm{4}\sqrt{\mathrm{2}}\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\:\:\:\frac{{dx}}{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\left\{\:\frac{\mathrm{3}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} \:−\mathrm{2}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\right\}} \\ $$$$=\mathrm{4}\sqrt{\mathrm{2}}\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\:\:\:\:\frac{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\left\{\:\mathrm{3}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} \:−\mathrm{2}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{2}} \right\}}{dx} \\ $$$$=\mathrm{4}\sqrt{\mathrm{2}}\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}\:−\mathrm{1}} \:\:\:\:\:\:\frac{{x}^{\mathrm{4}} \:+\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{1}}{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\left(\:\:\mathrm{3}{x}^{\mathrm{4}} \:+\mathrm{6}{x}^{\mathrm{2}} \:+\mathrm{3}\:−\mathrm{2}{x}^{\mathrm{4}} \:+\mathrm{4}{x}^{\mathrm{2}} \:−\mathrm{2}\right\}}{dx} \\ $$$$=\mathrm{4}\sqrt{\mathrm{2}}\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}\:−\mathrm{1}} \:\:\:\:\frac{{x}^{\mathrm{4}} \:+\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{1}}{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\left(\:{x}^{\mathrm{4}} \:+\mathrm{10}{x}^{\mathrm{2}} \:+\mathrm{1}\right)}{dx}….{be}\:{continued}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *