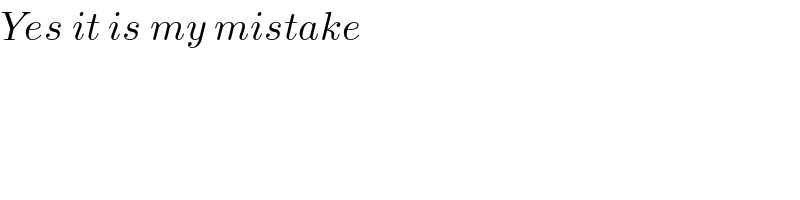Question Number 35241 by abdo mathsup 649 cc last updated on 17/May/18
$${calculate}\:\int_{\mathrm{0}} ^{\pi} \:\:\:\:\frac{{x}\:{dx}}{\mathrm{3}\:+{cosx}}\:\:. \\ $$
Commented by abdo.msup.com last updated on 17/May/18
![let put I=∫_0 ^π ((xdx)/(3 +cosx)) .changement tan((x/2))=t give x =2arctan(t) and I = ∫_0 ^∞ ((2arctan(t))/(3 +((1−t^2 )/(2+t^2 )))) ((2dt)/(1+t^2 )) = 4∫_0 ^∞ ((arctan(t))/(3 +3t^2 +1−t^2 ))dt =4 ∫_0 ^∞ ((arctan(t))/(4 +2t^2 ))dt=2∫_0 ^∞ ((arctan(t))/(2 +t^2 )) =_(t=x(√2)) 2∫_0 ^∞ ((arctan(x(√2)))/(2(1+x^2 )))(√2) dx =(√2) ∫_0 ^∞ ((arctan(x(√2)))/(1+x^2 ))dx let introduce the parametric function f(t) =∫_0 ^∞ ((arctan(tx))/(1+x^2 ))dx f^′ (t) = ∫_0 ^∞ (x/((1+t^2 x^2 )(1+x^2 )))dx =_(tx =u) ∫_0 ^∞ (u/(t(1+u^2 )(1+(u^2 /t^2 )))) (du/t) = ∫_0 ^∞ (u/((1+u^2 )(t^2 +u^2 )))du let decompose g(u)= (u/((u^2 +1)(u^2 +t^2 ))) g(u) = ((au +b)/(u^2 +1)) +((cu +d)/(u^2 +t^2 )) g(−u) =−g(u) ⇒b=d=0 so g(u)= ((au)/(u^2 +1)) +((cu)/(u^2 +t^2 )) lim_(u→+∞) u g(u)=0 = a+c ⇒c=−a g(u)= ((au)/(u^2 +1)) −((au)/(u^2 +t^2 )) g(1)=(1/(2(1+t^2 ))) = (a/2) −(a/(t^2 +1)) ⇒ (1/2) =(1/2)(1+t^2 )a −a ⇒ 1=(1+t^2 )a −2a =(t^2 −1)a ⇒ a= (1/(t^2 −1)) if t^2 ≠1 so g(u) = (1/(t^2 −1)) (u/(1+u^2 )) −(1/(t^2 −1)) (u/(t^2 +u^2 )) f^′ (t) =∫_0 ^∞ g(u)du =(1/(1−t^2 )){ ∫_0 ^∞ (u/(1+u^2 ))du −∫_0 ^∞ (u/(u^2 +t^2 ))du} = (1/(2(1−t^2 )))[ ln(1+u^2 )−ln(u^2 +t^2 )]_0 ^(+∞) = (1/(2(1−t^2 )))[ln(((u^2 +1)/(u^2 +t^2 )))]_0 ^(+∞) = (1/(2(1−t^2 ))) {ln(t^2 )= ((ln(t))/(1−t^2 )) f^′ (t) = ((ln(t))/(1−t^2 )) ⇒f(t)= ∫_0 ^t ((lnx)/(1−x^2 ))dx +λ λ=f(0)=0 ⇒ f(t)= ∫_0 ^t ((ln(x))/(1−x^2 ))dx I =(√2) f((√2))= (√2) ∫_0 ^(√2) ((ln(x))/(1−x^2 ))dx... be continued...](https://www.tinkutara.com/question/Q35283.png)
$${let}\:{put}\:{I}=\int_{\mathrm{0}} ^{\pi} \:\:\:\frac{{xdx}}{\mathrm{3}\:+{cosx}}\:.{changement} \\ $$$${tan}\left(\frac{{x}}{\mathrm{2}}\right)={t}\:{give}\:\:{x}\:=\mathrm{2}{arctan}\left({t}\right)\:{and} \\ $$$${I}\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\frac{\mathrm{2}{arctan}\left({t}\right)}{\mathrm{3}\:+\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{2}+{t}^{\mathrm{2}} }}\:\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$=\:\mathrm{4}\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{arctan}\left({t}\right)}{\mathrm{3}\:+\mathrm{3}{t}^{\mathrm{2}} \:+\mathrm{1}−{t}^{\mathrm{2}} }{dt} \\ $$$$=\mathrm{4}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{arctan}\left({t}\right)}{\mathrm{4}\:+\mathrm{2}{t}^{\mathrm{2}} }{dt}=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\:\frac{{arctan}\left({t}\right)}{\mathrm{2}\:+{t}^{\mathrm{2}} } \\ $$$$=_{{t}={x}\sqrt{\mathrm{2}}} \:\:\:\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{arctan}\left({x}\sqrt{\mathrm{2}}\right)}{\mathrm{2}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}\sqrt{\mathrm{2}}\:{dx} \\ $$$$=\sqrt{\mathrm{2}}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\frac{{arctan}\left({x}\sqrt{\mathrm{2}}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:{let}\:{introduce} \\ $$$${the}\:{parametric}\:{function} \\ $$$${f}\left({t}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{arctan}\left({tx}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$${f}^{'} \left({t}\right)\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{x}}{\left(\mathrm{1}+{t}^{\mathrm{2}} {x}^{\mathrm{2}} \right)\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{dx} \\ $$$$=_{{tx}\:={u}} \:\:\:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\frac{{u}}{{t}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\left(\mathrm{1}+\frac{{u}^{\mathrm{2}} }{{t}^{\mathrm{2}} }\right)}\:\frac{{du}}{{t}} \\ $$$$=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\:\frac{{u}}{\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\left({t}^{\mathrm{2}} \:+{u}^{\mathrm{2}} \right)}{du}\:\:{let} \\ $$$${decompose}\:{g}\left({u}\right)=\:\frac{{u}}{\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)\left({u}^{\mathrm{2}} \:+{t}^{\mathrm{2}} \right)} \\ $$$${g}\left({u}\right)\:=\:\frac{{au}\:+{b}}{{u}^{\mathrm{2}} \:+\mathrm{1}}\:\:+\frac{{cu}\:+{d}}{{u}^{\mathrm{2}} \:+{t}^{\mathrm{2}} } \\ $$$${g}\left(−{u}\right)\:=−{g}\left({u}\right)\:\Rightarrow{b}={d}=\mathrm{0}\:{so} \\ $$$${g}\left({u}\right)=\:\frac{{au}}{{u}^{\mathrm{2}} +\mathrm{1}}\:\:+\frac{{cu}}{{u}^{\mathrm{2}} \:+{t}^{\mathrm{2}} } \\ $$$${lim}_{{u}\rightarrow+\infty} \:{u}\:{g}\left({u}\right)=\mathrm{0}\:=\:{a}+{c}\:\Rightarrow{c}=−{a} \\ $$$${g}\left({u}\right)=\:\frac{{au}}{{u}^{\mathrm{2}} +\mathrm{1}}\:−\frac{{au}}{{u}^{\mathrm{2}} \:+{t}^{\mathrm{2}} } \\ $$$${g}\left(\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}\:=\:\frac{{a}}{\mathrm{2}}\:−\frac{{a}}{{t}^{\mathrm{2}} +\mathrm{1}}\:\Rightarrow \\ $$$$\:\frac{\mathrm{1}}{\mathrm{2}}\:=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+{t}^{\mathrm{2}} \right){a}\:−{a}\:\Rightarrow \\ $$$$\mathrm{1}=\left(\mathrm{1}+{t}^{\mathrm{2}} \right){a}\:−\mathrm{2}{a}\:=\left({t}^{\mathrm{2}} −\mathrm{1}\right){a}\:\Rightarrow \\ $$$${a}=\:\frac{\mathrm{1}}{{t}^{\mathrm{2}} −\mathrm{1}}\:\:\:\:{if}\:\:{t}^{\mathrm{2}} \neq\mathrm{1}\:\:{so} \\ $$$${g}\left({u}\right)\:=\:\frac{\mathrm{1}}{{t}^{\mathrm{2}} −\mathrm{1}}\:\frac{{u}}{\mathrm{1}+{u}^{\mathrm{2}} }\:−\frac{\mathrm{1}}{{t}^{\mathrm{2}} −\mathrm{1}}\:\frac{{u}}{{t}^{\mathrm{2}} +{u}^{\mathrm{2}} } \\ $$$${f}^{'} \left({t}\right)\:=\int_{\mathrm{0}} ^{\infty} \:{g}\left({u}\right){du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}−{t}^{\mathrm{2}} }\left\{\:\:\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{u}}{\mathrm{1}+{u}^{\mathrm{2}} }{du}\:−\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{u}}{{u}^{\mathrm{2}} \:+{t}^{\mathrm{2}} }{du}\right\} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)}\left[\:\:{ln}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)−{ln}\left({u}^{\mathrm{2}} \:+{t}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{+\infty} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)}\left[{ln}\left(\frac{{u}^{\mathrm{2}} +\mathrm{1}}{{u}^{\mathrm{2}} \:+{t}^{\mathrm{2}} }\right)\right]_{\mathrm{0}} ^{+\infty} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)}\:\left\{{ln}\left({t}^{\mathrm{2}} \right)=\:\frac{{ln}\left({t}\right)}{\mathrm{1}−{t}^{\mathrm{2}} }\right. \\ $$$${f}^{'} \left({t}\right)\:=\:\:\frac{{ln}\left({t}\right)}{\mathrm{1}−{t}^{\mathrm{2}} }\:\:\Rightarrow{f}\left({t}\right)=\:\int_{\mathrm{0}} ^{{t}} \:\:\frac{{lnx}}{\mathrm{1}−{x}^{\mathrm{2}} }{dx}\:+\lambda \\ $$$$\lambda={f}\left(\mathrm{0}\right)=\mathrm{0}\:\Rightarrow\:{f}\left({t}\right)=\:\int_{\mathrm{0}} ^{{t}} \:\:\:\frac{{ln}\left({x}\right)}{\mathrm{1}−{x}^{\mathrm{2}} }{dx} \\ $$$${I}\:=\sqrt{\mathrm{2}}\:{f}\left(\sqrt{\mathrm{2}}\right)=\:\sqrt{\mathrm{2}}\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}} \:\:\:\:\frac{{ln}\left({x}\right)}{\mathrm{1}−{x}^{\mathrm{2}} }{dx}… \\ $$$${be}\:{continued}… \\ $$
Commented by abdo.msup.com last updated on 17/May/18
$${error}\:\:{change}\:\mathrm{1}−{t}^{\mathrm{2}} \:{by}\:{t}^{\mathrm{2}} −\mathrm{1}\:{so} \\ $$$${f}\left({t}\right)=\:\int_{\mathrm{0}} ^{{t}} \:\:\:\frac{{ln}\left({x}\right)}{{x}^{\mathrm{2}} −\mathrm{1}}{dx} \\ $$$${I}\:=\sqrt{\mathrm{2}}\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}} \:\:\frac{{ln}\left({x}\right)}{{x}^{\mathrm{2}} −\mathrm{1}}{dx}. \\ $$
Commented by abdo mathsup 649 cc last updated on 20/May/18
![∫_0 ^(√2) ((lnx)/(x^2 −1))dx = −∫_0 ^1 ((lnx)/(1−x^2 ))dx +∫_1 ^(√2) ((lnx)/(x^2 −1))dx but ∫_0 ^1 ((ln(x))/(1−x^2 ))dx =∫_0 ^1 (Σ_(n=0) ^∞ x^(2n) )lnxdx =Σ_(n=0) ^∞ ∫_0 ^1 x^(2n) ln(x)dx by parts A_n = ∫_0 ^1 x^(2n) ln(x)dx =[(1/(2n+1))x^(2n+1) ln(x)]_0 ^1 − ∫_0 ^1 (1/(2n+1))x^(2n+1) (1/x)dx = −(1/((2n+1)^2 )) ∫_0 ^1 x^(2n) dx =−(1/((2n+1)^2 )) ⇒ ∫_0 ^1 ((ln(x))/(1−x^2 ))dx =−Σ_(n=0) ^∞ (1/((2n+1)^2 )) we have (π^2 /6) =Σ_(n=1) ^∞ (1/n^2 ) =Σ_(n=1) ^∞ (1/((2n)^2 )) +Σ_(n=0) ^∞ (1/((2n+1)^2 )) =(1/4) Σ_(n=1) ^∞ (1/n^2 ) +Σ_(n=0) ^∞ (1/((2n+1)^2 )) ⇒ Σ_(n=0) ^∞ (1/((2n+1)^2 )) = (3/4) Σ_(n=1) ^∞ (1/n^2 ) =(3/4) (π^2 /6) = (π^2 /8)](https://www.tinkutara.com/question/Q35522.png)
$$\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}} \:\:\:\frac{{lnx}}{{x}^{\mathrm{2}} −\mathrm{1}}{dx}\:=\:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{lnx}}{\mathrm{1}−{x}^{\mathrm{2}} }{dx}\:\:+\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \:\frac{{lnx}}{{x}^{\mathrm{2}} \:−\mathrm{1}}{dx}\:{but} \\ $$$$\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left({x}\right)}{\mathrm{1}−{x}^{\mathrm{2}} }{dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\left(\sum_{{n}=\mathrm{0}} ^{\infty} \:{x}^{\mathrm{2}{n}} \right){lnxdx} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:{x}^{\mathrm{2}{n}} \:{ln}\left({x}\right){dx}\:\:\:{by}\:{parts} \\ $$$${A}_{{n}} \:\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{\mathrm{2}{n}} \:{ln}\left({x}\right){dx}\:=\left[\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}{x}^{\mathrm{2}{n}+\mathrm{1}} {ln}\left({x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$−\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}{x}^{\mathrm{2}{n}+\mathrm{1}} \:\frac{\mathrm{1}}{{x}}{dx}\:=\:−\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:{x}^{\mathrm{2}{n}} {dx} \\ $$$$=−\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left({x}\right)}{\mathrm{1}−{x}^{\mathrm{2}} }{dx}\:=−\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${we}\:{have}\:\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{1}}{\left(\mathrm{2}{n}\right)^{\mathrm{2}} }\:+\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:+\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\:=\:\frac{\mathrm{3}}{\mathrm{4}}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:=\frac{\mathrm{3}}{\mathrm{4}}\:\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{8}} \\ $$
Commented by abdo mathsup 649 cc last updated on 20/May/18
![⇒ ∫_0 ^1 ((ln(x))/(x^2 −1))dx =−(π^2 /8) changement x=(1/t) give ∫_1 ^(√2) ((ln(x))/(x^2 −1))dx = ∫_1 ^(1/( (√2))) ((−ln(t))/(( (1/t^2 ) −1))) (−(dt/t^2 )) = −∫_(1/( (√2))) ^1 ((ln(t))/(1−t^2 ))dt =−∫_(1/( (√2))) ^1 (Σ_(n=0) ^∞ t^(2n) )ln(t)dt =−Σ_(n=0) ^∞ ∫_(1/( (√2))) ^1 t^(2n) ln(t)dt =−Σ_(n=0) ^∞ A_n by parts A_(n ) = [ (1/(2n+1))t^(2n+1) ln(t)]_(1/( (√2))) ^1 − ∫_(1/( (√2))) ^1 (1/(2n+1))t^(2n) dt =(1/(2n+1))((1/( (√2))))^(2n+1) ln((√2)) −(1/((2n+1)^2 )) ⇒ Σ_(n=0) ^∞ A_n = ln((√2))Σ_(n=0) ^∞ (1/(2n+1))((1/( (√2))))^(2n+1) −Σ_(n=0) ^∞ (1/((2n+1)^2 )) ⇒ ∫_1 ^(√2) ((ln(x))/(x^2 −1))dx = ln((√2))Σ_(n=0) ^∞ (1/((2n+1)^2 ))((1/( (√2))))^(2n+1) −(π^2 /8)](https://www.tinkutara.com/question/Q35523.png)
$$\Rightarrow\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{ln}\left({x}\right)}{{x}^{\mathrm{2}} −\mathrm{1}}{dx}\:=−\frac{\pi^{\mathrm{2}} }{\mathrm{8}} \\ $$$${changement}\:{x}=\frac{\mathrm{1}}{{t}}\:{give} \\ $$$$\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \:\:\:\:\frac{{ln}\left({x}\right)}{{x}^{\mathrm{2}} −\mathrm{1}}{dx}\:=\:\:\int_{\mathrm{1}} ^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} \:\:\:\:\frac{−{ln}\left({t}\right)}{\left(\:\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\:−\mathrm{1}\right)}\:\left(−\frac{{dt}}{{t}^{\mathrm{2}} }\right) \\ $$$$=\:−\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} ^{\mathrm{1}} \:\:\:\:\frac{{ln}\left({t}\right)}{\mathrm{1}−{t}^{\mathrm{2}} }{dt}\:\:\:=−\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} ^{\mathrm{1}} \:\left(\sum_{{n}=\mathrm{0}} ^{\infty} \:{t}^{\mathrm{2}{n}} \right){ln}\left({t}\right){dt} \\ $$$$=−\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} ^{\mathrm{1}} \:\:{t}^{\mathrm{2}{n}} \:{ln}\left({t}\right){dt}\:=−\sum_{{n}=\mathrm{0}} ^{\infty} \:{A}_{{n}} \:\:\:{by}\:{parts} \\ $$$${A}_{{n}\:} =\:\:\left[\:\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}{t}^{\mathrm{2}{n}+\mathrm{1}} {ln}\left({t}\right)\right]_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} ^{\mathrm{1}} \:−\:\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} ^{\mathrm{1}} \:\:\:\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}{t}^{\mathrm{2}{n}} {dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}{n}+\mathrm{1}} {ln}\left(\sqrt{\mathrm{2}}\right)\:−\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\sum_{{n}=\mathrm{0}} ^{\infty} \:\:{A}_{{n}} \:\:=\:{ln}\left(\sqrt{\mathrm{2}}\right)\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}{n}+\mathrm{1}} \:−\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\:\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \:\:\:\frac{{ln}\left({x}\right)}{{x}^{\mathrm{2}} −\mathrm{1}}{dx}\:=\:{ln}\left(\sqrt{\mathrm{2}}\right)\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}{n}+\mathrm{1}} \:\: \\ $$$$−\frac{\pi^{\mathrm{2}} }{\mathrm{8}} \\ $$$$ \\ $$
Commented by prof Abdo imad last updated on 20/May/18
$$\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \:\:\:\:\frac{{ln}\left({x}\right)}{{x}^{\mathrm{2}} −\mathrm{1}}{dx}\:=\:{ln}\left(\sqrt{\mathrm{2}}\right)\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}{n}+\mathrm{1}} −\frac{\pi^{\mathrm{2}} }{\mathrm{8}} \\ $$$${let}\:{calculate}\:{the}\:{value}\:{of}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}{n}+\mathrm{1}} \\ $$$${let}\:{put}\:{S}\left({x}\right)=\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}{x}^{\mathrm{2}{n}+\mathrm{1}} \:\:{with}\:\mid{x}\mid<\mathrm{1} \\ $$$${S}^{'} \left({x}\right)\:=\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:{x}^{\mathrm{2}{n}} \:\:=\:\frac{\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{2}} }\:\Rightarrow\:{S}\left({x}\right)=\:\int\:\frac{{dx}}{\mathrm{1}−{x}^{\mathrm{2}} }\:+{c} \\ $$$${S}\left({x}\right)=\:\frac{\mathrm{1}}{\mathrm{2}}\int\:\left\{\:\:\frac{\mathrm{1}}{\mathrm{1}−{x}}\:+\frac{\mathrm{1}}{\mathrm{1}+{x}}\right\}{dx}\:+{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}\mid\:+{c}\:\:{we}\:{have}\:{S}\left({o}\right)=\mathrm{0}\:\Rightarrow{c}=\mathrm{0}\:\Rightarrow \\ $$$${S}\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}\mid\:{and} \\ $$$$\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}{n}+\mathrm{1}} \:=\:{S}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)\: \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid\:\frac{\mathrm{1}\:+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}}{\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}}\mid\:=\:\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{\sqrt{\mathrm{2}}\:+\mathrm{1}}{\:\sqrt{\mathrm{2}}\:−\mathrm{1}}\right)\:\Rightarrow \\ $$$$\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \:\:\:\:\:\frac{{ln}\left({x}\right)}{{x}^{\mathrm{2}} −\mathrm{1}}{dx}\:=\frac{{ln}\left(\sqrt{\mathrm{2}}\right)}{\mathrm{2}}{ln}\left(\frac{\sqrt{\mathrm{2}}\:+\mathrm{1}}{\:\sqrt{\mathrm{2}}\:−\mathrm{1}}\right)\:−\frac{\pi^{\mathrm{2}} }{\mathrm{8}} \\ $$
Commented by prof Abdo imad last updated on 20/May/18
$${so}\:{I}\:=\sqrt{\mathrm{2}}\:\:\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}} \:\:\:\frac{{ln}\left({x}\right)}{{x}^{\mathrm{2}} \:−\mathrm{1}}{dx} \\ $$$$=\sqrt{\mathrm{2}}\left\{\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{ln}\left({x}\right)}{{x}^{\mathrm{2}} −\mathrm{1}}{dx}\:+\:\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \:\:\:\frac{{ln}\left({x}\right)}{{x}^{\mathrm{2}} \:−\mathrm{1}}{dx}\right\} \\ $$$$=\sqrt{\mathrm{2}_{} }\:\left\{\:−\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\:\:+\frac{{ln}\left(\sqrt{\mathrm{2}}\right)}{\mathrm{2}}{ln}\left(\frac{\sqrt{\mathrm{2}}\:+\mathrm{1}}{\:\sqrt{\mathrm{2}}\:−\mathrm{1}}\right)\:−\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\right\} \\ $$$${I}\:=\sqrt{\mathrm{2}}\left\{\:\:\frac{{ln}\left(\sqrt{\mathrm{2}}\right)}{\mathrm{2}}{ln}\left(\frac{\sqrt{\mathrm{2}}\:+\mathrm{1}}{\:\sqrt{\mathrm{2}}\:−\mathrm{1}}\right)\:−\frac{\pi^{\mathrm{2}} }{\mathrm{4}}\right\} \\ $$
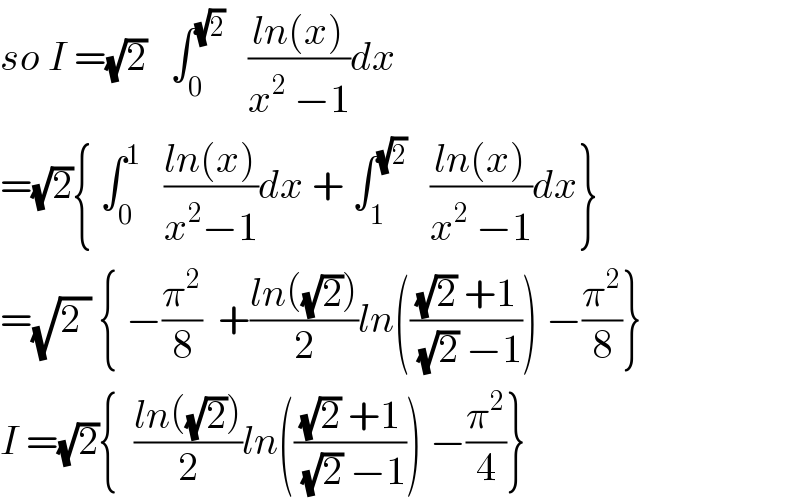
Answered by math1967 last updated on 17/May/18
![∫_(0 ) ^π ((xdx)/(3+2cos^2 (x/2)−1))=∫_(0 ) ^π ((xdx)/(2(1+cos^2 (x/2)))) now 2I=π∫_0 ^π (dx/(2(1+cos^2 (x/2)))) =(π/2)∫_0 ^π ((sec^2 (x/2)dx)/(sec^2 (x/2)+1)) =π∫_0 ^π (((1/2)sec^2 (x/2)dx)/(2+tan^2 (x/2))) =π∫_0 ^π ((d(tan(x/2)))/(((√2))^2 +tan^2 (x/2)))=π[(1/( (√2)))tan^(−1) tan (x/(2(√2)))]_0 ^π =π×[(1/( (√2)))×(π/(2(√2)))]=(π^2 /4)∴I=(π^2 /8) plz. check](https://www.tinkutara.com/question/Q35261.png)
$$\underset{\mathrm{0}\:} {\overset{\pi} {\int}}\frac{{xdx}}{\mathrm{3}+\mathrm{2cos}\:^{\mathrm{2}} \frac{{x}}{\mathrm{2}}−\mathrm{1}}=\underset{\mathrm{0}\:} {\overset{\pi} {\int}}\frac{{xdx}}{\mathrm{2}\left(\mathrm{1}+\mathrm{cos}\:^{\mathrm{2}} \frac{{x}}{\mathrm{2}}\right)} \\ $$$${now}\:\mathrm{2}{I}=\pi\underset{\mathrm{0}} {\overset{\pi} {\int}}\frac{{dx}}{\mathrm{2}\left(\mathrm{1}+{cos}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}\right)} \\ $$$$=\frac{\pi}{\mathrm{2}}\underset{\mathrm{0}} {\overset{\pi} {\int}}\frac{\mathrm{sec}\:^{\mathrm{2}} \frac{{x}}{\mathrm{2}}{dx}}{\mathrm{sec}\:^{\mathrm{2}} \frac{{x}}{\mathrm{2}}+\mathrm{1}} \\ $$$$=\pi\underset{\mathrm{0}} {\overset{\pi} {\int}}\frac{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sec}\:^{\mathrm{2}} \frac{{x}}{\mathrm{2}}{dx}}{\mathrm{2}+{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}} \\ $$$$=\pi\underset{\mathrm{0}} {\overset{\pi} {\int}}\frac{{d}\left({tan}\frac{{x}}{\mathrm{2}}\right)}{\left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}} +{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}=\pi\left[\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{tan}^{−\mathrm{1}} \mathrm{tan}\:\frac{{x}}{\mathrm{2}\sqrt{\mathrm{2}}}\right]_{\mathrm{0}} ^{\pi} \\ $$$$=\pi×\left[\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}×\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2}}}\right]=\frac{\pi^{\mathrm{2}} }{\mathrm{4}}\therefore{I}=\frac{\pi^{\mathrm{2}} }{\mathrm{8}} \\ $$$${plz}.\:{check} \\ $$
Commented by MJS last updated on 17/May/18
$$\mathrm{in}\:\mathrm{this}\:\mathrm{case}\:\mathrm{if}\:{f}\left({x}\right)=\frac{\frac{{x}}{\mathrm{2}}}{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:\frac{{x}}{\mathrm{2}}}\:\Rightarrow \\ $$$$\Rightarrow\:{f}\left(\pi−{x}\right)=\frac{\frac{\pi−{x}}{\mathrm{2}}}{\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \:\frac{{x}}{\mathrm{2}}} \\ $$$$\mathrm{and}\:\mathrm{we}\:\mathrm{get}\:{f}\left({x}\right)+{f}\left(\pi−{x}\right)= \\ $$$$=\frac{\mathrm{3}\pi}{\mathrm{8}+\mathrm{sin}^{\mathrm{2}} \:{x}}+\frac{\pi\mathrm{cos}\:{x}}{\mathrm{8}+\mathrm{sin}^{\mathrm{2}} \:{x}}−\frac{\mathrm{2}{x}\mathrm{cos}\:{x}}{\mathrm{8}+\mathrm{sin}^{\mathrm{2}} \:{x}} \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{solve}\:\mathrm{the}\:\mathrm{1}^{\mathrm{st}} \:\mathrm{and}\:\mathrm{2}^{\mathrm{nd}} \:\mathrm{but}\:\mathrm{the}\:\mathrm{3}^{\mathrm{rd}} \:\mathrm{looks} \\ $$$$\mathrm{nasty}\:\mathrm{again}… \\ $$
Commented by math1967 last updated on 17/May/18
$${OK}\:{thanks} \\ $$
Answered by math1967 last updated on 17/May/18
![2I=∫_0 ^π ((xdx)/(3+cosx))+∫_0 ^π (((π−x)dx)/(3+cos(π−x))) =π∫_0 ^π ((6dx)/((3+cosx)(3−cosx))) =6π∫_0 ^π (dx/(9−cos^2 x))=6π∫_0 ^π ((sec^2 xdx)/(9sec^2 x−1)) =6π∫_0 ^π ((sec^2 xdx)/(8+9tan^2 x))=2π∫_0 ^π ((3sec^2 xdx)/((2(√(2 )))^2 +(3tan x)^2 )) =2π∫_0 ^π ((d(3tanx))/((2(√2))^2 +(3tan x)^2 )) =2π[(1/(2(√2)))tan^(−1) ((3tan x)/(2(√2)))]_0 ^π =2π[(1/(2(√2)))×(π/2) −0] =(π^2 /(2(√2))) ∴ I=(π^2 /(4(√2)))](https://www.tinkutara.com/question/Q35254.png)
$$\mathrm{2}{I}=\underset{\mathrm{0}} {\overset{\pi} {\int}}\frac{{xdx}}{\mathrm{3}+{cosx}}+\underset{\mathrm{0}} {\overset{\pi} {\int}}\frac{\left(\pi−{x}\right){dx}}{\mathrm{3}+{cos}\left(\pi−{x}\right)} \\ $$$$=\pi\underset{\mathrm{0}} {\overset{\pi} {\int}}\frac{\mathrm{6}{dx}}{\left(\mathrm{3}+{cosx}\right)\left(\mathrm{3}−{cosx}\right)} \\ $$$$=\mathrm{6}\pi\underset{\mathrm{0}} {\overset{\pi} {\int}}\frac{{dx}}{\mathrm{9}−{cos}^{\mathrm{2}} {x}}=\mathrm{6}\pi\underset{\mathrm{0}} {\overset{\pi} {\int}}\frac{\mathrm{sec}\:^{\mathrm{2}} {xdx}}{\mathrm{9}{sec}^{\mathrm{2}} {x}−\mathrm{1}} \\ $$$$=\mathrm{6}\pi\underset{\mathrm{0}} {\overset{\pi} {\int}}\frac{{sec}^{\mathrm{2}} {xdx}}{\mathrm{8}+\mathrm{9tan}\:^{\mathrm{2}} {x}}=\mathrm{2}\pi\underset{\mathrm{0}} {\overset{\pi} {\int}}\frac{\mathrm{3sec}\:^{\mathrm{2}} {xdx}}{\left(\mathrm{2}\sqrt{\mathrm{2}\:\:}\right)^{\mathrm{2}} +\left(\mathrm{3tan}\:{x}\right)^{\mathrm{2}} } \\ $$$$=\mathrm{2}\pi\underset{\mathrm{0}} {\overset{\pi} {\int}}\frac{{d}\left(\mathrm{3}{tanx}\right)}{\left(\mathrm{2}\sqrt{\mathrm{2}}\right)^{\mathrm{2}} +\left(\mathrm{3tan}\:{x}\right)^{\mathrm{2}} } \\ $$$$=\mathrm{2}\pi\left[\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{3tan}\:{x}}{\mathrm{2}\sqrt{\mathrm{2}}}\right]_{\mathrm{0}} ^{\pi} \\ $$$$=\mathrm{2}\pi\left[\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}×\frac{\pi}{\mathrm{2}}\:−\mathrm{0}\right] \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{2}\sqrt{\mathrm{2}}}\:\therefore\:{I}=\frac{\pi^{\mathrm{2}} }{\mathrm{4}\sqrt{\mathrm{2}}} \\ $$
Commented by MJS last updated on 17/May/18
$$\mathrm{this}\:\mathrm{seems}\:\mathrm{wrong}: \\ $$$$\frac{{x}}{\mathrm{3}+\mathrm{cos}\:{x}}+\frac{\pi−{x}}{\mathrm{3}+\mathrm{cos}\:\left(\pi−{x}\right)}=\frac{{x}}{\mathrm{3}+\mathrm{cos}\:{x}}+\frac{\pi−{x}}{\mathrm{3}−\mathrm{cos}\:{x}}= \\ $$$$=\frac{\mathrm{3}\pi+\left(\pi−\mathrm{2}{x}\right)\mathrm{cos}\:{x}}{\mathrm{9}−\mathrm{cos}^{\mathrm{2}} \:{x}}\neq\frac{\mathrm{6}\pi}{\mathrm{9}−\mathrm{cos}^{\mathrm{2}} \:{x}} \\ $$$$\mathrm{please}\:\mathrm{explain} \\ $$$$\frac{\pi^{\mathrm{2}} }{\mathrm{4}\sqrt{\mathrm{2}}}\approx\mathrm{1}.\mathrm{744716} \\ $$$$\mathrm{but}\:\mathrm{I}\:\mathrm{get}\:\underset{\mathrm{0}} {\overset{\pi} {\int}}\frac{{x}}{\mathrm{3}+\mathrm{cos}\:{x}}{dx}\approx\mathrm{1}.\mathrm{988159} \\ $$
Commented by math1967 last updated on 17/May/18
$${Yes}\:{it}\:{is}\:{my}\:{mistake} \\ $$$$ \\ $$