Question Number 63033 by mathmax by abdo last updated on 28/Jun/19
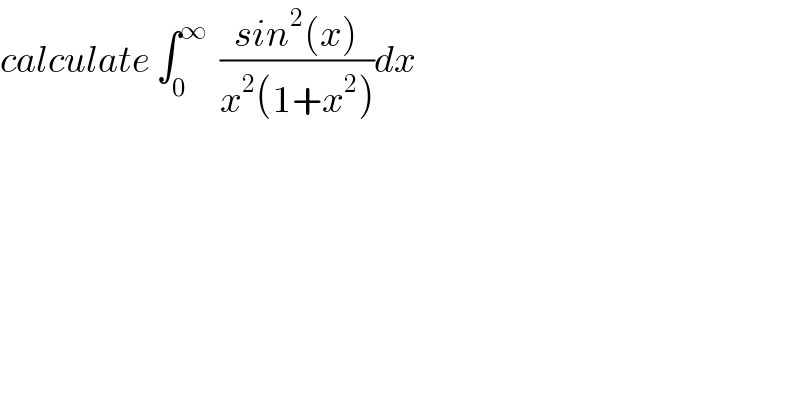
$${calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{sin}^{\mathrm{2}} \left({x}\right)}{{x}^{\mathrm{2}} \left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{dx}\: \\ $$
Commented by mathmax by abdo last updated on 28/Jun/19
![let A =∫_0 ^∞ ((sin^2 x)/(x^2 (1+x^2 ))) dx ⇒ A =∫_0 ^∞ sin^2 x{(1/x^2 ) −(1/(1+x^2 ))}dx =∫_0 ^∞ ((sin^2 x)/x^2 )dx −∫_0 ^∞ ((sin^2 x)/(1+x^2 ))dx =H−K by parts H =[−(1/x)sin^2 x]_0 ^(+∞) −∫_0 ^∞ −(1/x)2sinx cosxdx =∫_0 ^∞ ((sin(2x))/x)dx =_(2x=t) ∫_0 ^∞ ((sin(t))/(t/2)) (dt/2) =∫_0 ^∞ ((sint)/t)dt =(π/2) (result proved) K =∫_0 ^∞ ((1−cos(2x))/(2(1+x^2 )))dx =(1/2)∫_0 ^∞ (dx/(1+x^2 )) −(1/2)∫_0 ^∞ ((cos(2x))/(1+x^2 ))dx =(π/4) −(1/4)∫_(−∞) ^(+∞) ((cos(2x))/(1+x^2 ))dx ∫_(−∞) ^(+∞) ((cos(2x))/(1+x^2 ))dx =Re(∫_(−∞) ^(+∞) (e^(i2x) /(x^2 +1))dx) let W(z) =(e^(i2z) /(z^2 +1)) the poles of W are +^− i residus theorem give ∫_(−∞) ^(+∞) W(z)dz =2iπ Res(W,i) =2iπ (e^(−2) /(2i)) =(π/e^2 ) ⇒ ∫_(−∞) ^(+∞) ((cos(2x))/(1+x^2 ))dx =(π/e^2 ) ⇒ K =(π/4)−(π/(4e^2 )) ⇒ A =(π/2) −(π/4) +(π/(4e^2 )) =(π/4) +(π/(4e^2 )) ⇒ A =(π/4)(1+(1/e^2 )).](https://www.tinkutara.com/question/Q63069.png)
$${let}\:{A}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{sin}^{\mathrm{2}} {x}}{{x}^{\mathrm{2}} \left(\mathrm{1}+{x}^{\mathrm{2}} \right)}\:{dx}\:\Rightarrow\:{A}\:=\int_{\mathrm{0}} ^{\infty} \:{sin}^{\mathrm{2}} {x}\left\{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:−\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }\right\}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\frac{{sin}^{\mathrm{2}} {x}}{{x}^{\mathrm{2}} }{dx}\:−\int_{\mathrm{0}} ^{\infty} \frac{{sin}^{\mathrm{2}} {x}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:={H}−{K} \\ $$$${by}\:{parts}\:{H}\:=\left[−\frac{\mathrm{1}}{{x}}{sin}^{\mathrm{2}} {x}\right]_{\mathrm{0}} ^{+\infty} \:−\int_{\mathrm{0}} ^{\infty} \:\:−\frac{\mathrm{1}}{{x}}\mathrm{2}{sinx}\:{cosxdx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{sin}\left(\mathrm{2}{x}\right)}{{x}}{dx}\:=_{\mathrm{2}{x}={t}} \:\:\:\:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{sin}\left({t}\right)}{\frac{{t}}{\mathrm{2}}}\:\frac{{dt}}{\mathrm{2}}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{{sint}}{{t}}{dt}\:=\frac{\pi}{\mathrm{2}}\:\:\left({result}\:{proved}\right) \\ $$$${K}\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{1}−{cos}\left(\mathrm{2}{x}\right)}{\mathrm{2}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} }\:−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{{cos}\left(\mathrm{2}{x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$=\frac{\pi}{\mathrm{4}}\:−\frac{\mathrm{1}}{\mathrm{4}}\int_{−\infty} ^{+\infty} \:\:\:\frac{{cos}\left(\mathrm{2}{x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$\int_{−\infty} ^{+\infty} \:\frac{{cos}\left(\mathrm{2}{x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:={Re}\left(\int_{−\infty} ^{+\infty} \:\:\frac{{e}^{{i}\mathrm{2}{x}} }{{x}^{\mathrm{2}} \:+\mathrm{1}}{dx}\right)\:{let}\:{W}\left({z}\right)\:=\frac{{e}^{{i}\mathrm{2}{z}} }{{z}^{\mathrm{2}} \:+\mathrm{1}}\:{the}\:{poles}\:{of}\:{W}\:{are}\:\overset{−} {+}{i} \\ $$$${residus}\:{theorem}\:{give} \\ $$$$\int_{−\infty} ^{+\infty} \:\:{W}\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:{Res}\left({W},{i}\right)\:=\mathrm{2}{i}\pi\:\frac{{e}^{−\mathrm{2}} }{\mathrm{2}{i}}\:\:=\frac{\pi}{{e}^{\mathrm{2}} }\:\Rightarrow\:\int_{−\infty} ^{+\infty} \:\frac{{cos}\left(\mathrm{2}{x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:=\frac{\pi}{{e}^{\mathrm{2}} }\:\Rightarrow \\ $$$${K}\:=\frac{\pi}{\mathrm{4}}−\frac{\pi}{\mathrm{4}{e}^{\mathrm{2}} }\:\Rightarrow\:{A}\:=\frac{\pi}{\mathrm{2}}\:−\frac{\pi}{\mathrm{4}}\:+\frac{\pi}{\mathrm{4}{e}^{\mathrm{2}} }\:=\frac{\pi}{\mathrm{4}}\:+\frac{\pi}{\mathrm{4}{e}^{\mathrm{2}} }\:\:\Rightarrow \\ $$$${A}\:=\frac{\pi}{\mathrm{4}}\left(\mathrm{1}+\frac{\mathrm{1}}{{e}^{\mathrm{2}} }\right). \\ $$
