Menu Close

calculate-0-x-2-2cosx-1-x-4-x-2-1-dx-

Tinku Tara 0 Comments
Pin




Question Number 48720 by Abdo msup. last updated on 27/Nov/18
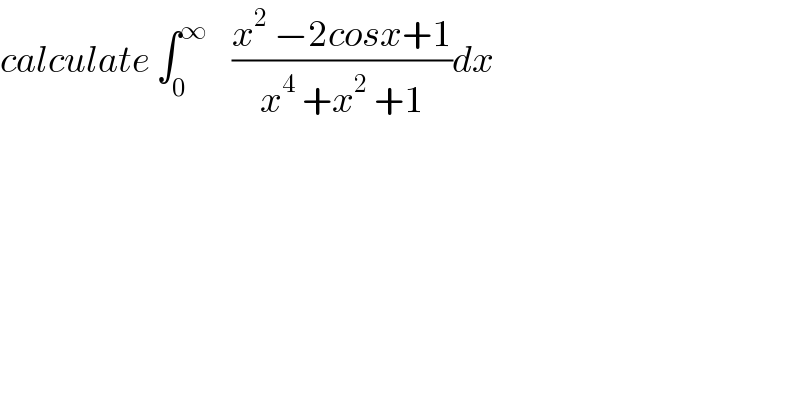
calculate ∫_0 ^∞ ((x^2 −2cosx+1)/(x^4 +x^2 +1))dx
$${calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{x}^{\mathrm{2}} \:−\mathrm{2}{cosx}+\mathrm{1}}{{x}^{\mathrm{4}} \:+{x}^{\mathrm{2}} \:+\mathrm{1}}{dx} \\ $$
Commented by Abdo msup. last updated on 28/Nov/18
let I = ∫_0 ^∞ ((x^2 −2cosx +1)/(x^4 +x^2 +1))dx ⇒ 2I =∫_(−∞) ^(+∞) ((x^2 +1)/(x^4 +x^2 +1))dx −∫_(−∞) ^(+∞) ((2cosx)/(x^4 +x^2 +1))dx=H−K let find H let ϕ(z)=((z^2 +1)/(z^4 +z^2 +1)) poles of ϕ? z^4 +z^2 +1=0 ⇒t^2 +t+1=0 (t=z^2 ) Δ=−3=(i(√3))^2 ⇒z_1 =((−1+i(√3))/2) =e^((i2π)/3) and z_2 =e^(−((i2π)/3)) z^2 =e^((i2π)/3) ⇒ z =+^− e^((iπ)/3) z^2 =e^(−((i2π)/3)) ⇒z =+^− e^(−((iπ)/3)) ⇒ ϕ(z)=((z^2 +1)/((z−e^((iπ)/3) )(z+e^((iπ)/3) )(z−e^(−((iπ)/3)) )(z+e^(−((iπ)/3)) ))) ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ{ Res(ϕ,e^((iπ)/3) ) +Res(ϕ,−e^(−((iπ)/3)) ) Res(ϕ,e^((iπ)/3) )=((e^(2((iπ)/3)) +1)/(2e^((iπ)/3) (2isin((π/3))(2cos((π/3))))) =((e^((iπ)/3) +e^(−((iπ)/3)) )/(8i sin((π/3))cos((π/3)))) =((2cos((π/3)))/(8isin((π/3))cos((π/3)))) =(1/(4i((√3)/2))) =(1/(2i(√3))) Res(ϕ,−e^(−((iπ)/3)) ) =((e^(−((2iπ)/3)) +1)/(−2cos((π/3))(2isin((π/3)))(−2e^(−((iπ)/3)) ))) =((e^((iπ)/3) +e^((−iπ)/3) )/(8i cos((π/3))sin((π/3)))) =((2cos((π/3)))/(8i cos((π/3))sin((π/3)))) =(1/(4isin((π/3)))) = (1/(4i ((√3)/2))) =(1/(2i(√3))) ⇒ ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ{ (1/(2i(√3))) +(1/(2i(√3)))} =((2π)/( (√3))) =H
$${let}\:{I}\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{x}^{\mathrm{2}} −\mathrm{2}{cosx}\:+\mathrm{1}}{{x}^{\mathrm{4}} \:+{x}^{\mathrm{2}} \:+\mathrm{1}}{dx}\:\Rightarrow \\ $$$$\mathrm{2}{I}\:=\int_{−\infty} ^{+\infty} \:\frac{{x}^{\mathrm{2}} \:+\mathrm{1}}{{x}^{\mathrm{4}} \:+{x}^{\mathrm{2}} \:+\mathrm{1}}{dx}\:−\int_{−\infty} ^{+\infty} \:\:\frac{\mathrm{2}{cosx}}{{x}^{\mathrm{4}} \:+{x}^{\mathrm{2}} \:+\mathrm{1}}{dx}={H}−{K} \\ $$$${let}\:{find}\:{H}\:{let}\:\varphi\left({z}\right)=\frac{{z}^{\mathrm{2}} \:+\mathrm{1}}{{z}^{\mathrm{4}} \:+{z}^{\mathrm{2}} \:+\mathrm{1}}\:{poles}\:{of}\:\varphi? \\ $$$${z}^{\mathrm{4}} \:+{z}^{\mathrm{2}} \:+\mathrm{1}=\mathrm{0}\:\Rightarrow{t}^{\mathrm{2}} \:+{t}+\mathrm{1}=\mathrm{0}\:\:\left({t}={z}^{\mathrm{2}} \right) \\ $$$$\Delta=−\mathrm{3}=\left({i}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \:\Rightarrow{z}_{\mathrm{1}} =\frac{−\mathrm{1}+{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\:={e}^{\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \:\:{and}\:{z}_{\mathrm{2}} ={e}^{−\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \\ $$$${z}^{\mathrm{2}} ={e}^{\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \:\Rightarrow\:{z}\:=\overset{−} {+}\:{e}^{\frac{{i}\pi}{\mathrm{3}}} \\ $$$${z}^{\mathrm{2}} ={e}^{−\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \:\Rightarrow{z}\:=\overset{−} {+}\:{e}^{−\frac{{i}\pi}{\mathrm{3}}} \:\Rightarrow \\ $$$$\varphi\left({z}\right)=\frac{{z}^{\mathrm{2}} \:+\mathrm{1}}{\left({z}−{e}^{\frac{{i}\pi}{\mathrm{3}}} \right)\left({z}+{e}^{\frac{{i}\pi}{\mathrm{3}}} \right)\left({z}−{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)\left({z}+{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)} \\ $$$$\int_{−\infty} ^{+\infty} \:\:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{\:{Res}\left(\varphi,{e}^{\frac{{i}\pi}{\mathrm{3}}} \right)\:+{Res}\left(\varphi,−{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)\right. \\ $$$${Res}\left(\varphi,{e}^{\frac{{i}\pi}{\mathrm{3}}} \right)=\frac{{e}^{\mathrm{2}\frac{{i}\pi}{\mathrm{3}}} +\mathrm{1}}{\mathrm{2}{e}^{\frac{{i}\pi}{\mathrm{3}}} \left(\mathrm{2}{isin}\left(\frac{\pi}{\mathrm{3}}\right)\left(\mathrm{2}{cos}\left(\frac{\pi}{\mathrm{3}}\right)\right)\right.} \\ $$$$=\frac{{e}^{\frac{{i}\pi}{\mathrm{3}}} \:+{e}^{−\frac{{i}\pi}{\mathrm{3}}} }{\mathrm{8}{i}\:{sin}\left(\frac{\pi}{\mathrm{3}}\right){cos}\left(\frac{\pi}{\mathrm{3}}\right)}\:=\frac{\mathrm{2}{cos}\left(\frac{\pi}{\mathrm{3}}\right)}{\mathrm{8}{isin}\left(\frac{\pi}{\mathrm{3}}\right){cos}\left(\frac{\pi}{\mathrm{3}}\right)}\:=\frac{\mathrm{1}}{\mathrm{4}{i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\:=\frac{\mathrm{1}}{\mathrm{2}{i}\sqrt{\mathrm{3}}} \\ $$$${Res}\left(\varphi,−{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)\:=\frac{{e}^{−\frac{\mathrm{2}{i}\pi}{\mathrm{3}}} +\mathrm{1}}{−\mathrm{2}{cos}\left(\frac{\pi}{\mathrm{3}}\right)\left(\mathrm{2}{isin}\left(\frac{\pi}{\mathrm{3}}\right)\right)\left(−\mathrm{2}{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)} \\ $$$$=\frac{{e}^{\frac{{i}\pi}{\mathrm{3}}} \:+{e}^{\frac{−{i}\pi}{\mathrm{3}}} }{\mathrm{8}{i}\:{cos}\left(\frac{\pi}{\mathrm{3}}\right){sin}\left(\frac{\pi}{\mathrm{3}}\right)}\:=\frac{\mathrm{2}{cos}\left(\frac{\pi}{\mathrm{3}}\right)}{\mathrm{8}{i}\:{cos}\left(\frac{\pi}{\mathrm{3}}\right){sin}\left(\frac{\pi}{\mathrm{3}}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}{isin}\left(\frac{\pi}{\mathrm{3}}\right)}\:=\:\frac{\mathrm{1}}{\mathrm{4}{i}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\:=\frac{\mathrm{1}}{\mathrm{2}{i}\sqrt{\mathrm{3}}}\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{\:\frac{\mathrm{1}}{\mathrm{2}{i}\sqrt{\mathrm{3}}}\:+\frac{\mathrm{1}}{\mathrm{2}{i}\sqrt{\mathrm{3}}}\right\}\:=\frac{\mathrm{2}\pi}{\:\sqrt{\mathrm{3}}}\:={H} \\ $$
Commented by Abdo msup. last updated on 28/Nov/18
let find K K = ∫_(−∞) ^(+∞) ((2cosx)/(x^4 +x^2 +1))dx =Re(∫_(−∞) ^(+∞) ((2 e^(ix) )/(x^(4 ) +x^2 +1))dx) let W(z) =((2 e^(iz) )/(z^4 +z^2 +1)) ⇒ W(z)=((2 e^(iz) )/(z^4 +z^2 +1)) ⇒W(z) =((2 e^(iz) )/((z−e^((iπ)/3) )(z +e^((iπ)/3) )(z−e^(−((iπ)/3)) )(z+e^(−((iπ)/3)) ))) ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ { Res(ϕ,e^((iπ)/3) ) +Res(ϕ,−e^(−((iπ)/3)) )} Res(ϕ,e^((iπ)/3) ) = ((2 e^(i(cos(π/3)+isin((π/3)))) )/(2 e^((iπ)/3) (2i sin((π/3)))2cos((π/3)))) = (e^(i((1/2)+i((√3)/2))) /(4isin((π/3))cos((π/3)))) e^(−((iπ)/3)) =((e^(−((√3)/2)) e^(i((1/2)−(π/3))) )/(4i((√3)/2).(1/2))) =(e^(−((√3)/2)) /(i(√3))) e^(i((1/2)−(π/3))) Res(ϕ,−e^(−((iπ)/3)) ) = ((2 e^(i(cos(π/3)−isin((π/3)))) )/(−2cos((π/3))(2isin((π/3))(−2 e^((−iπ)/3) ))) =(e^(i((1/2)−i((√3)/2))) /(4i cos((π/3))sin((π/3)))) e^((iπ)/3) =((e^((√3)/2) e^(i((1/2)+(π/3))) )/(4i (1/2) ((√3)/2))) = ((e^((√3)/(2 )) e^(i((1/2)+(π/3))) )/(i(√3))) ⇒ ∫_(−∞) ^(+∞) W(z)dz =2iπ(1/(i(√3))){ e^(−((√3)/2)) e^(i((1/2)−(π/3))) + e^((√3)/2) e^(i((1/2)+(π/3){) } =((2π)/( (√3))){ e^(−((√3)/2)) {cos((1/2)−(π/3))+isin((1/2)−(π/3))+ e^((√3)/2) { cos((1/2)+(π/3))+i sin((1/2)+(π/3))}} K =Re(∫_(−∞) ^(+∞) W(z)dz) =((2π)/( (√3))){ e^(−((√3)/2)) cos((1/2)−(π/3)) +e^((√3)/2) cos((1/2) +(π/3))} so thevalue of I is determined.
$${let}\:{find}\:{K} \\ $$$${K}\:=\:\int_{−\infty} ^{+\infty} \:\frac{\mathrm{2}{cosx}}{{x}^{\mathrm{4}} \:+{x}^{\mathrm{2}} \:+\mathrm{1}}{dx}\:={Re}\left(\int_{−\infty} ^{+\infty} \:\frac{\mathrm{2}\:{e}^{{ix}} }{{x}^{\mathrm{4}\:} \:+{x}^{\mathrm{2}} \:+\mathrm{1}}{dx}\right) \\ $$$${let}\:{W}\left({z}\right)\:=\frac{\mathrm{2}\:{e}^{{iz}} }{{z}^{\mathrm{4}} \:+{z}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow \\ $$$${W}\left({z}\right)=\frac{\mathrm{2}\:{e}^{{iz}} }{{z}^{\mathrm{4}} \:+{z}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow{W}\left({z}\right)\:=\frac{\mathrm{2}\:{e}^{{iz}} }{\left({z}−{e}^{\frac{{i}\pi}{\mathrm{3}}} \right)\left({z}\:+{e}^{\frac{{i}\pi}{\mathrm{3}}} \right)\left({z}−{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)\left({z}+{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)} \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:\left\{\:{Res}\left(\varphi,{e}^{\frac{{i}\pi}{\mathrm{3}}} \right)\:+{Res}\left(\varphi,−{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)\right\} \\ $$$${Res}\left(\varphi,{e}^{\frac{{i}\pi}{\mathrm{3}}} \right)\:=\:\frac{\mathrm{2}\:{e}^{{i}\left({cos}\frac{\pi}{\mathrm{3}}+{isin}\left(\frac{\pi}{\mathrm{3}}\right)\right)} }{\mathrm{2}\:{e}^{\frac{{i}\pi}{\mathrm{3}}} \left(\mathrm{2}{i}\:{sin}\left(\frac{\pi}{\mathrm{3}}\right)\right)\mathrm{2}{cos}\left(\frac{\pi}{\mathrm{3}}\right)} \\ $$$$=\:\frac{{e}^{{i}\left(\frac{\mathrm{1}}{\mathrm{2}}+{i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)} }{\mathrm{4}{isin}\left(\frac{\pi}{\mathrm{3}}\right){cos}\left(\frac{\pi}{\mathrm{3}}\right)}\:{e}^{−\frac{{i}\pi}{\mathrm{3}}} \:\:=\frac{{e}^{−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}} \:{e}^{{i}\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\pi}{\mathrm{3}}\right)} }{\mathrm{4}{i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}.\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$=\frac{{e}^{−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}} }{{i}\sqrt{\mathrm{3}}}\:{e}^{{i}\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\pi}{\mathrm{3}}\right)} \\ $$$${Res}\left(\varphi,−{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)\:=\:\frac{\mathrm{2}\:{e}^{{i}\left({cos}\frac{\pi}{\mathrm{3}}−{isin}\left(\frac{\pi}{\mathrm{3}}\right)\right)} }{−\mathrm{2}{cos}\left(\frac{\pi}{\mathrm{3}}\right)\left(\mathrm{2}{isin}\left(\frac{\pi}{\mathrm{3}}\right)\left(−\mathrm{2}\:{e}^{\frac{−{i}\pi}{\mathrm{3}}} \right)\right.} \\ $$$$=\frac{{e}^{{i}\left(\frac{\mathrm{1}}{\mathrm{2}}−{i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)} }{\mathrm{4}{i}\:{cos}\left(\frac{\pi}{\mathrm{3}}\right){sin}\left(\frac{\pi}{\mathrm{3}}\right)}\:{e}^{\frac{{i}\pi}{\mathrm{3}}} \:=\frac{{e}^{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}} \:{e}^{{i}\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\pi}{\mathrm{3}}\right)} }{\mathrm{4}{i}\:\frac{\mathrm{1}}{\mathrm{2}}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\:=\:\frac{{e}^{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}\:}} \:\:{e}^{{i}\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\pi}{\mathrm{3}}\right)} }{{i}\sqrt{\mathrm{3}}}\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:{W}\left({z}\right){dz}\:=\mathrm{2}{i}\pi\frac{\mathrm{1}}{{i}\sqrt{\mathrm{3}}}\left\{\:\:{e}^{−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}} \:{e}^{{i}\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\pi}{\mathrm{3}}\right)} \:+\:{e}^{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}} \:{e}^{{i}\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\pi}{\mathrm{3}}\left\{\right.\right.} \right\} \\ $$$$=\frac{\mathrm{2}\pi}{\:\sqrt{\mathrm{3}}}\left\{\:{e}^{−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}} \left\{{cos}\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\pi}{\mathrm{3}}\right)+{isin}\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\pi}{\mathrm{3}}\right)+\right.\right. \\ $$$$\left.{e}^{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}} \left\{\:{cos}\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\pi}{\mathrm{3}}\right)+{i}\:{sin}\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\pi}{\mathrm{3}}\right)\right\}\right\} \\ $$$${K}\:={Re}\left(\int_{−\infty} ^{+\infty} {W}\left({z}\right){dz}\right) \\ $$$$=\frac{\mathrm{2}\pi}{\:\sqrt{\mathrm{3}}}\left\{\:{e}^{−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}} {cos}\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\pi}{\mathrm{3}}\right)\:+{e}^{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}} {cos}\left(\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\pi}{\mathrm{3}}\right)\right\} \\ $$$${so}\:{thevalue}\:{of}\:{I}\:{is}\:{determined}. \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *